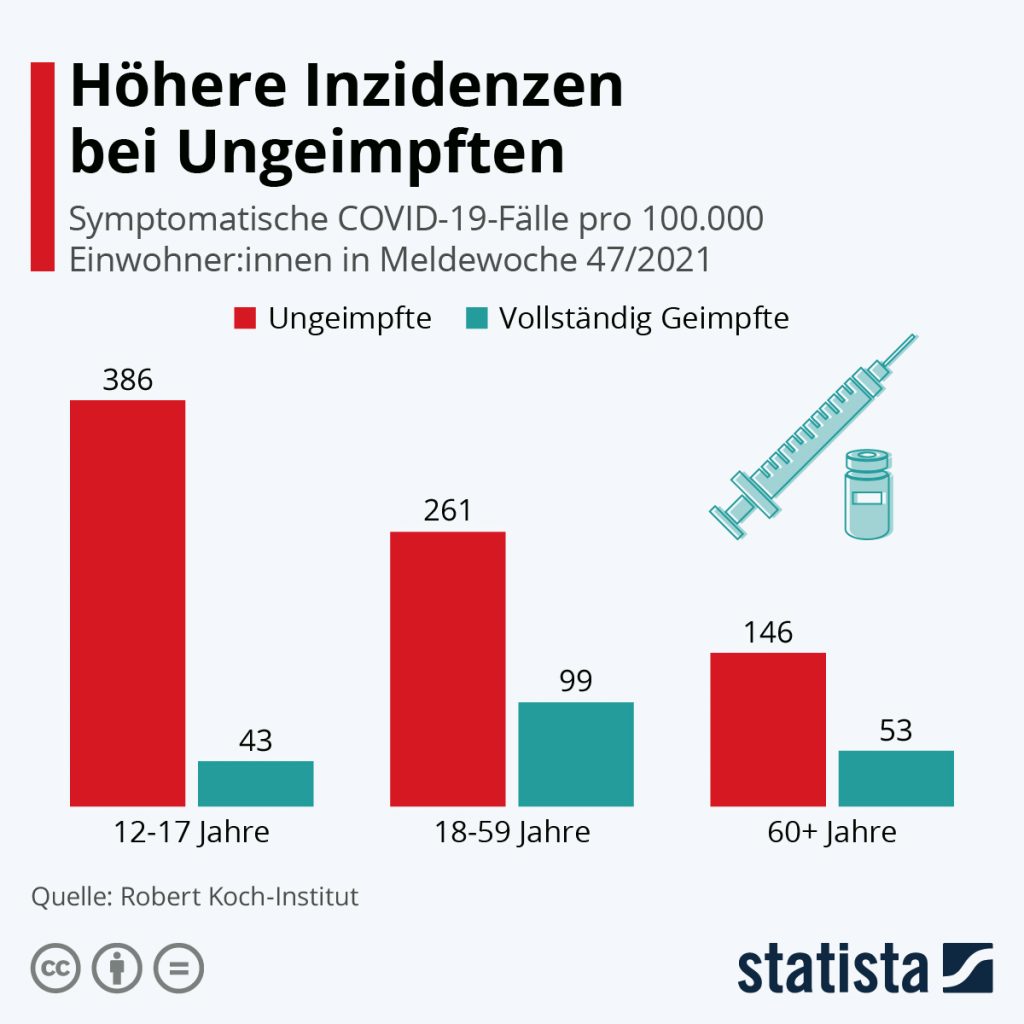
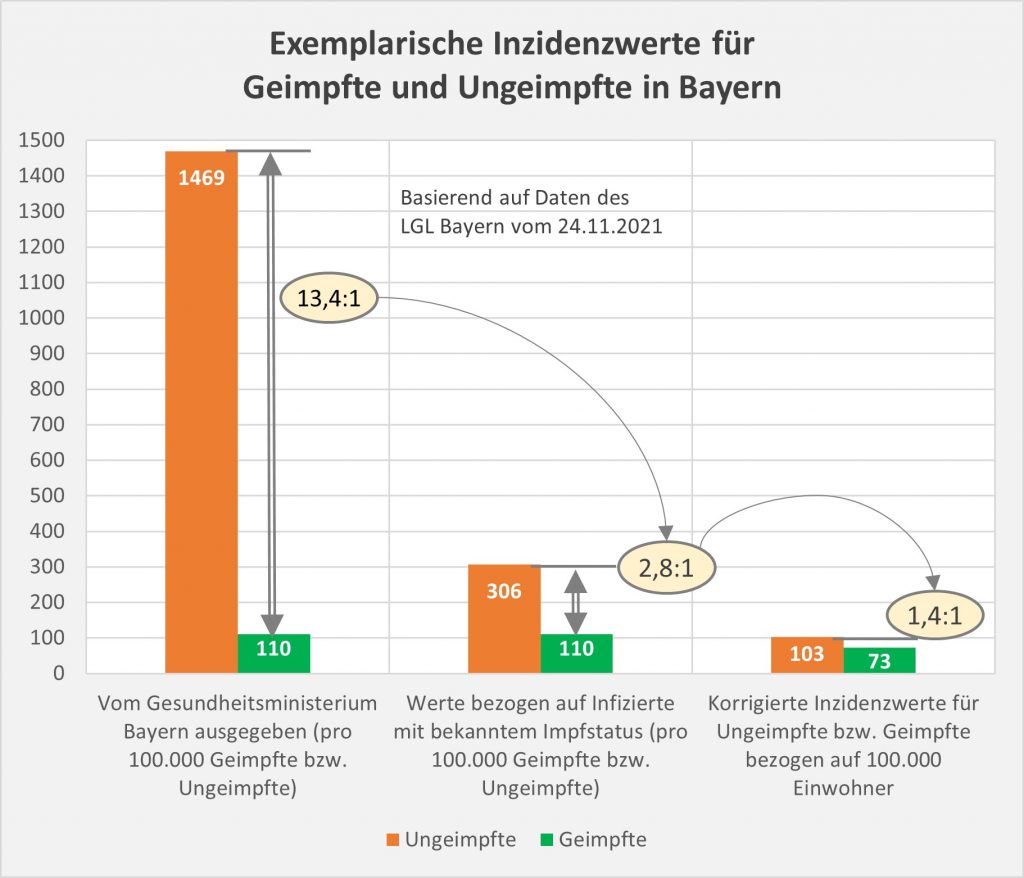
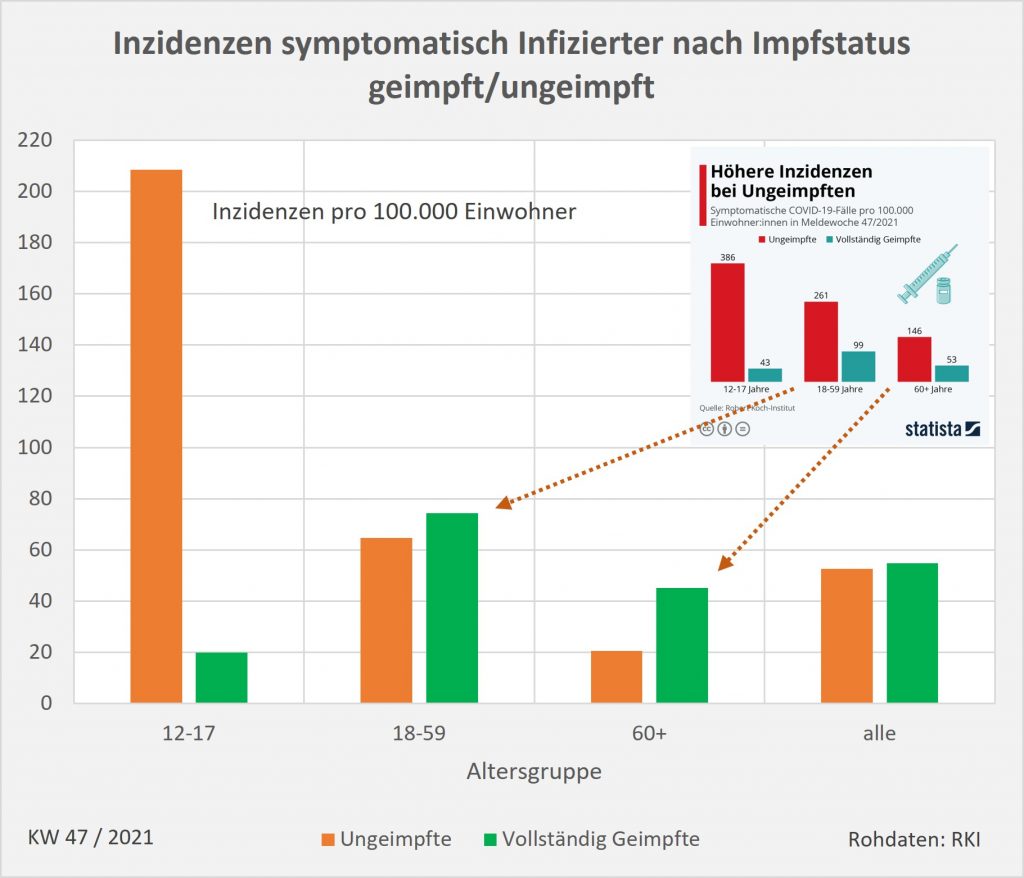
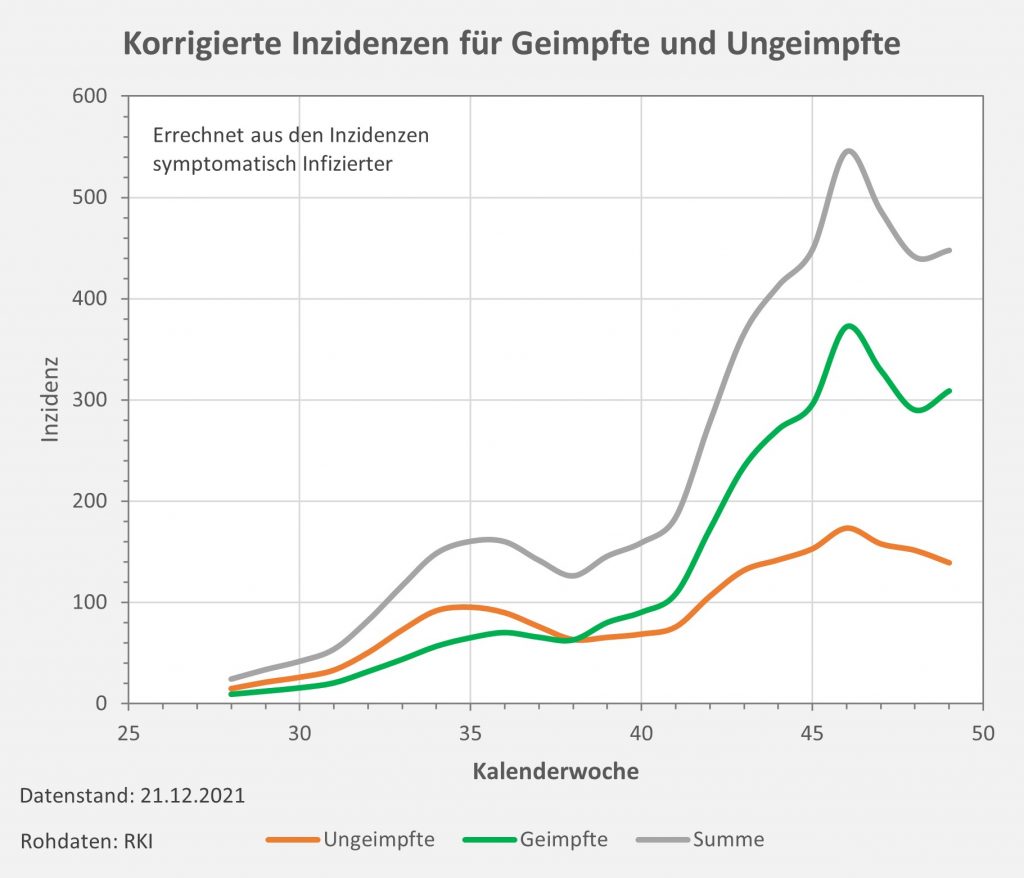
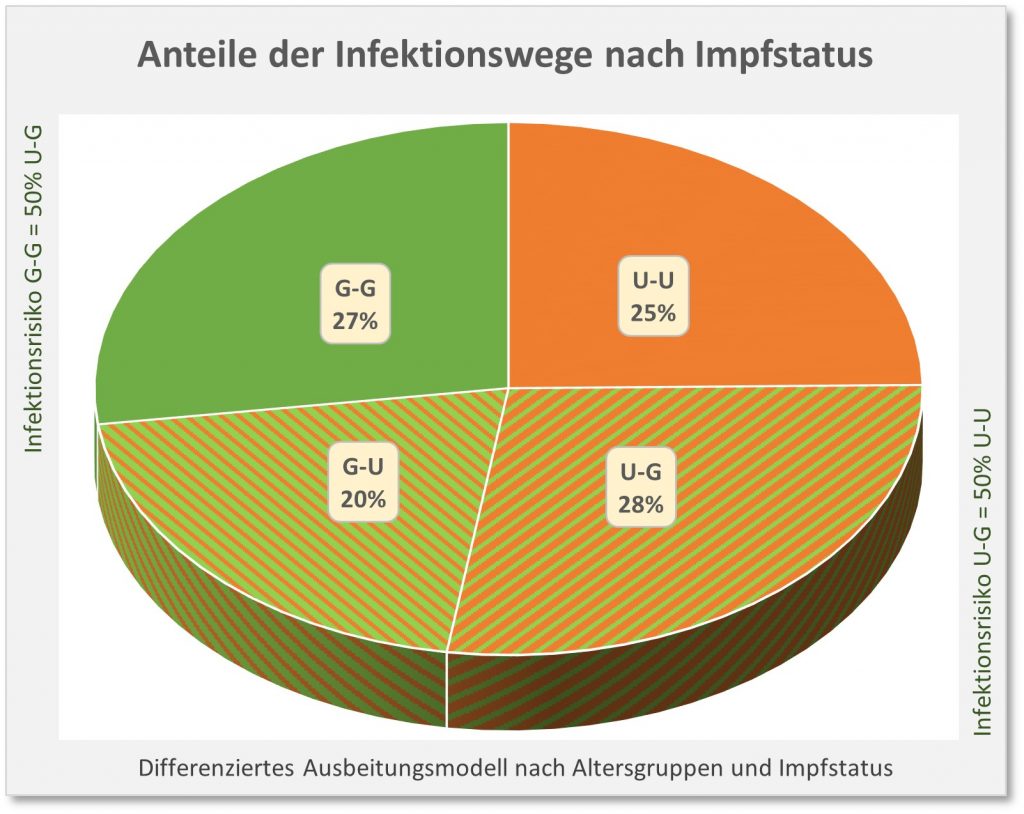
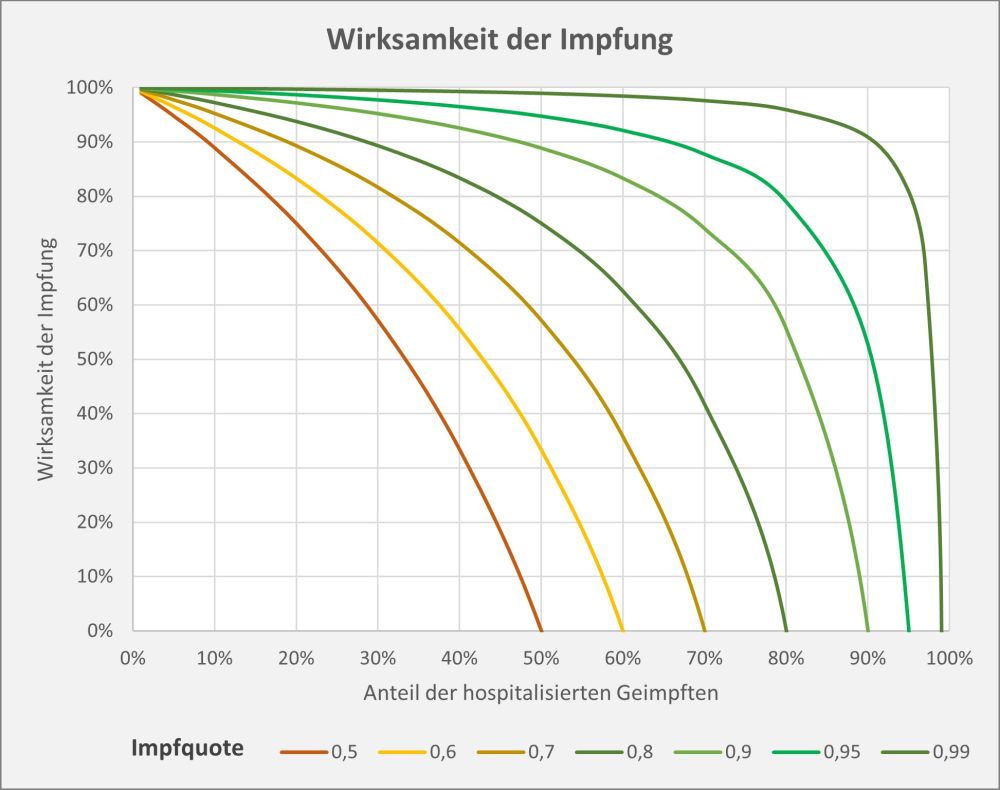
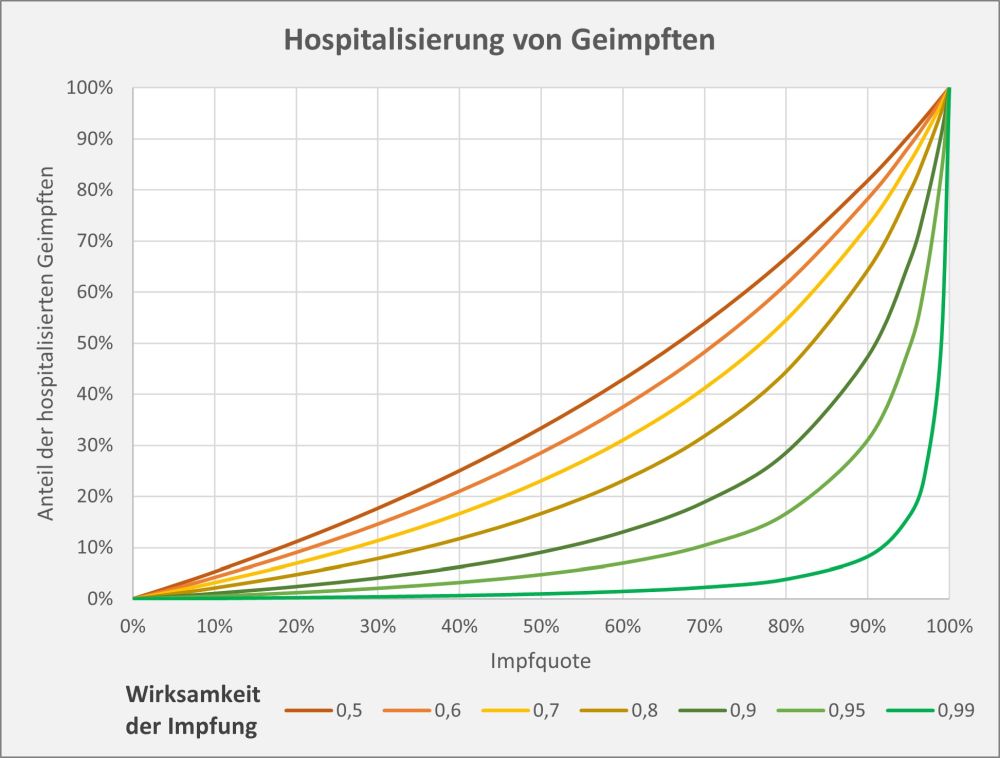
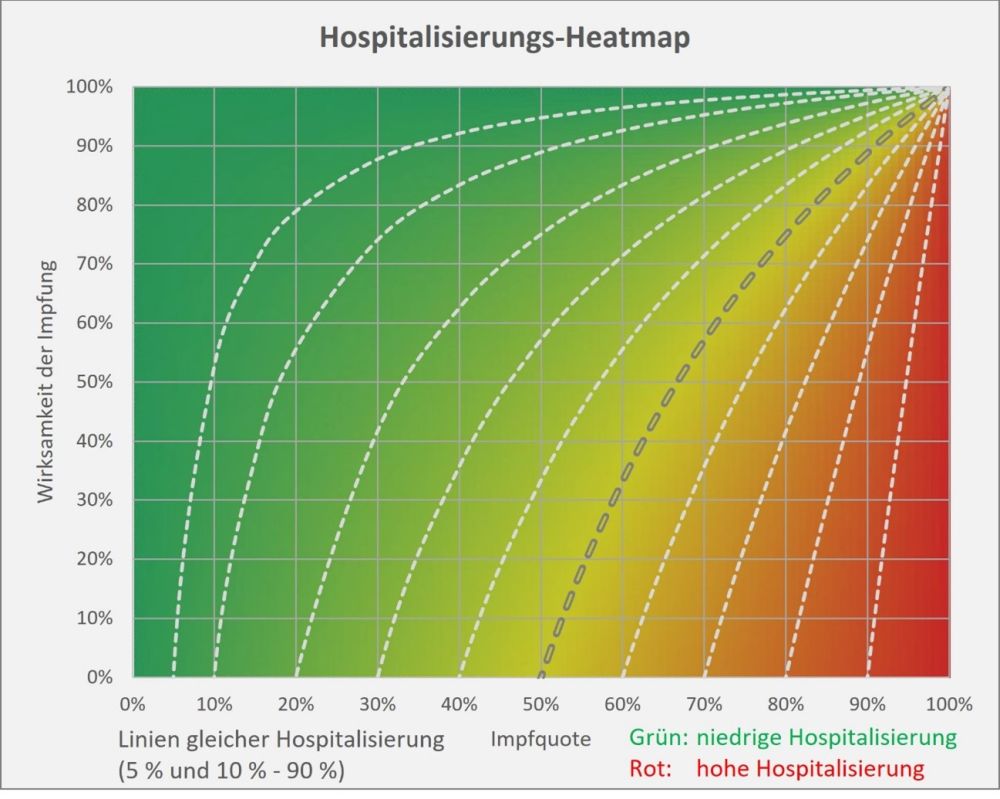
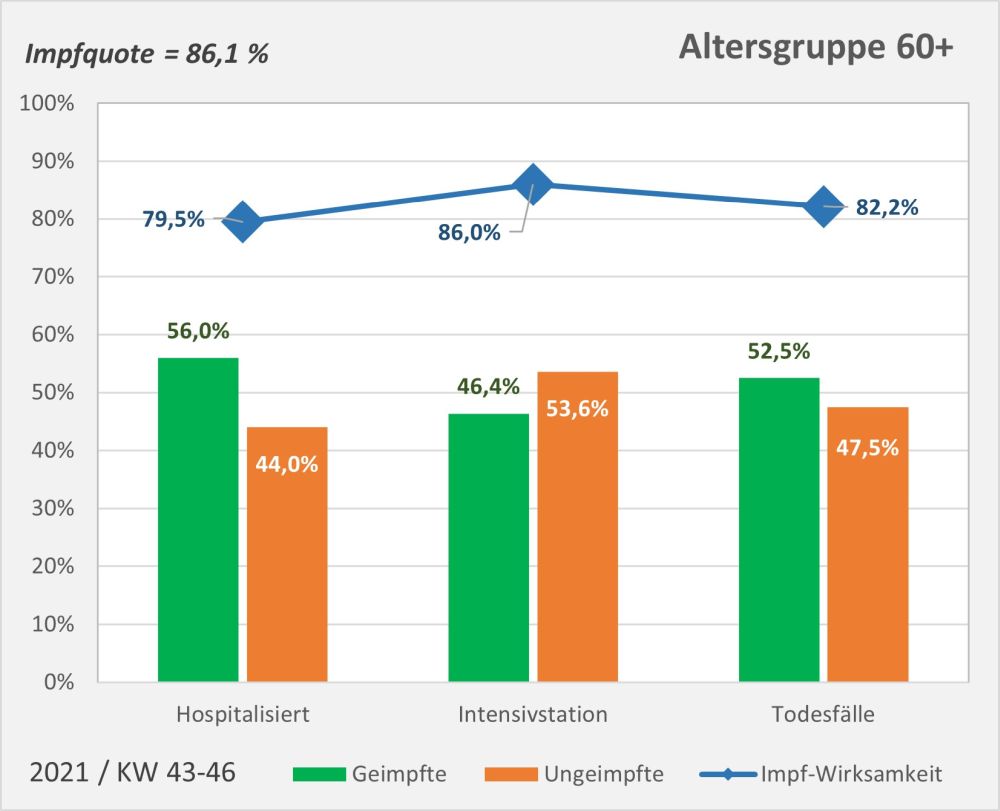
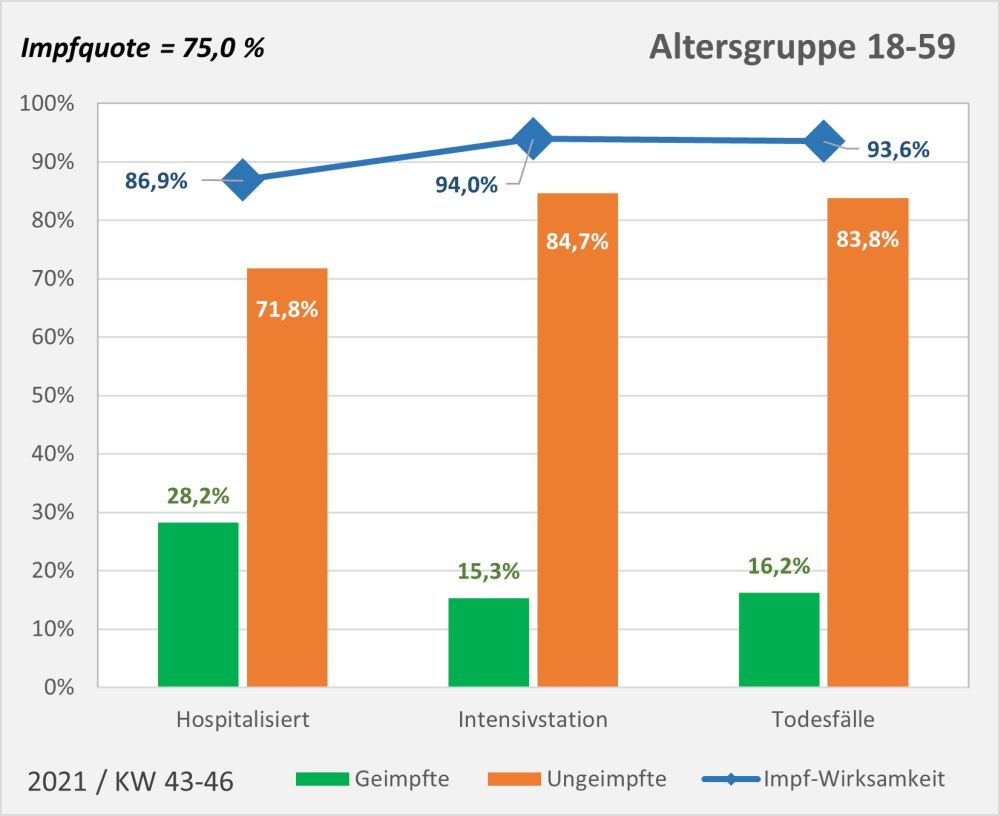
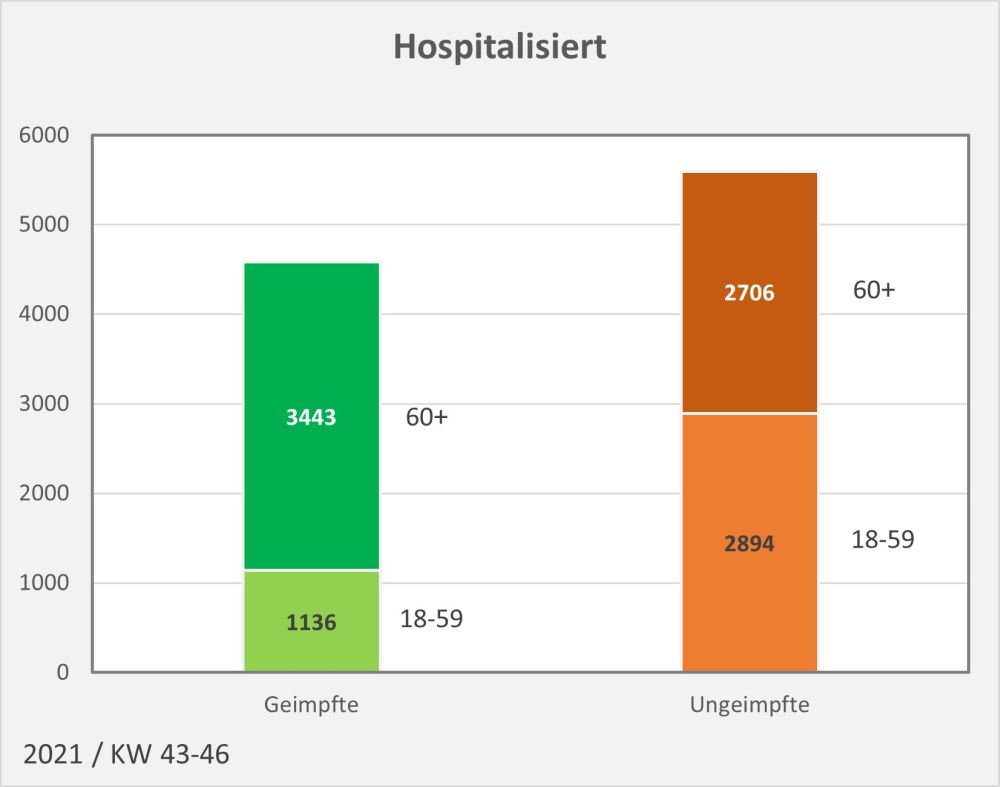
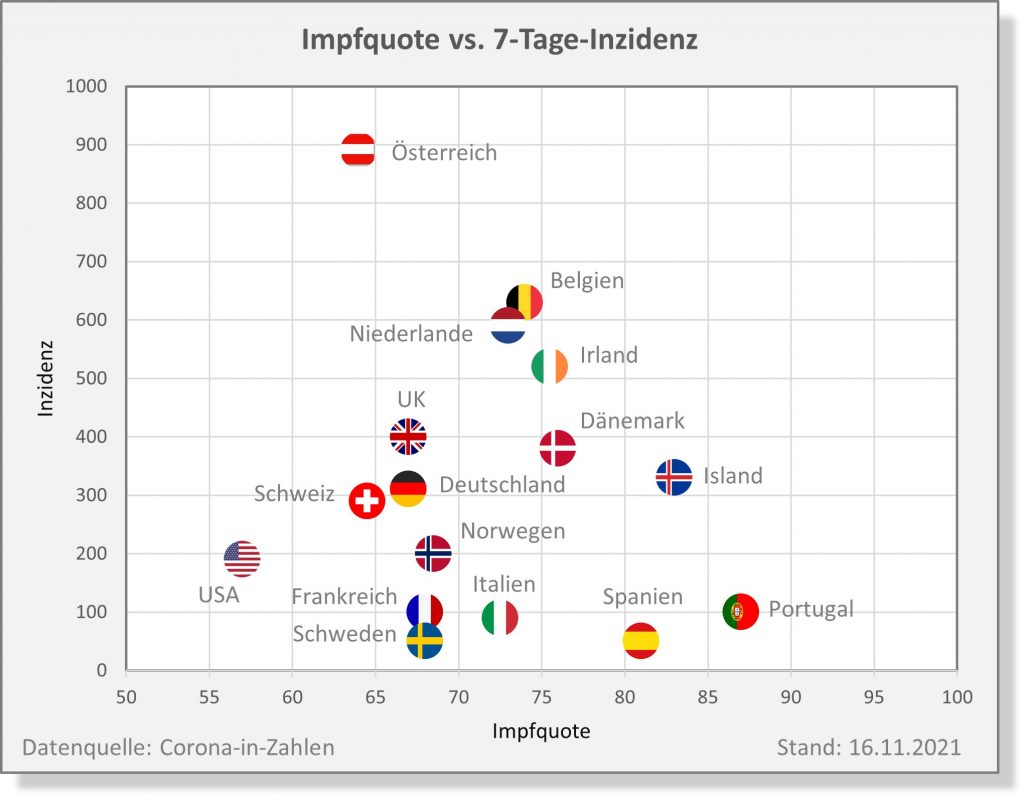
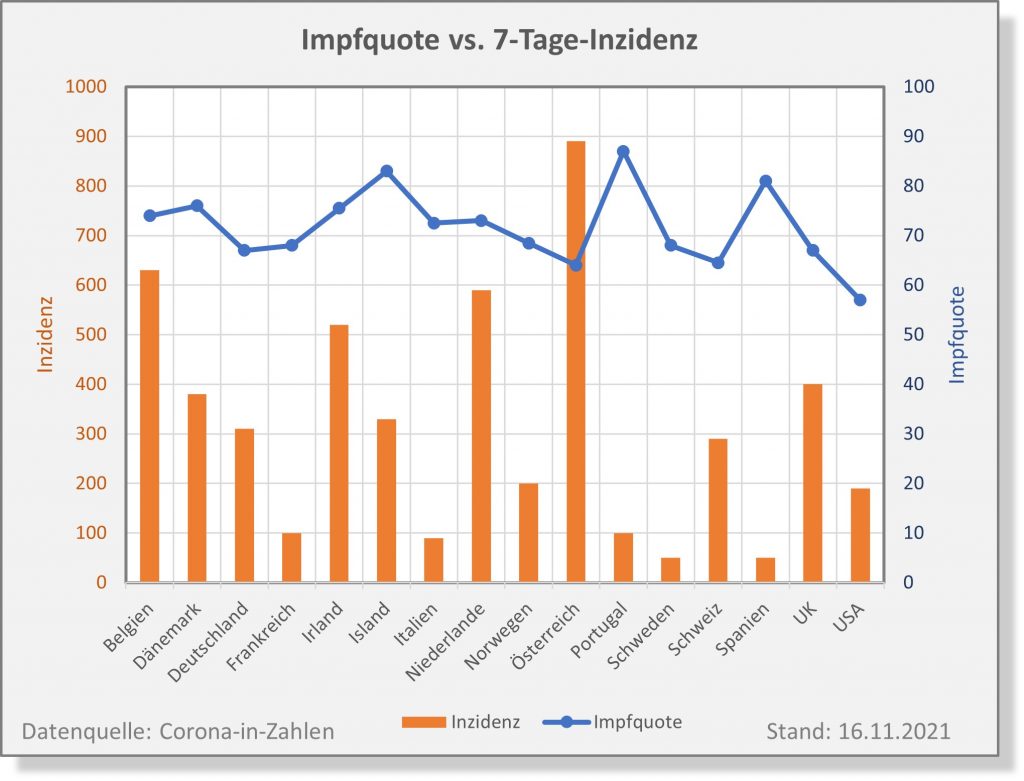
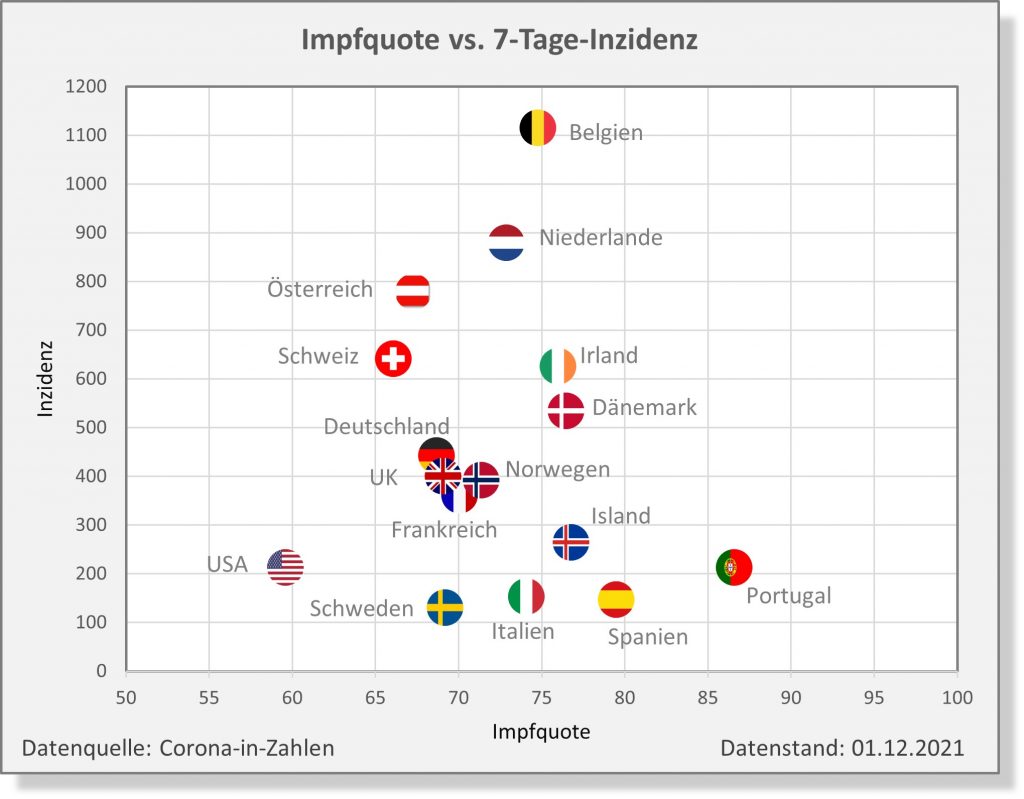
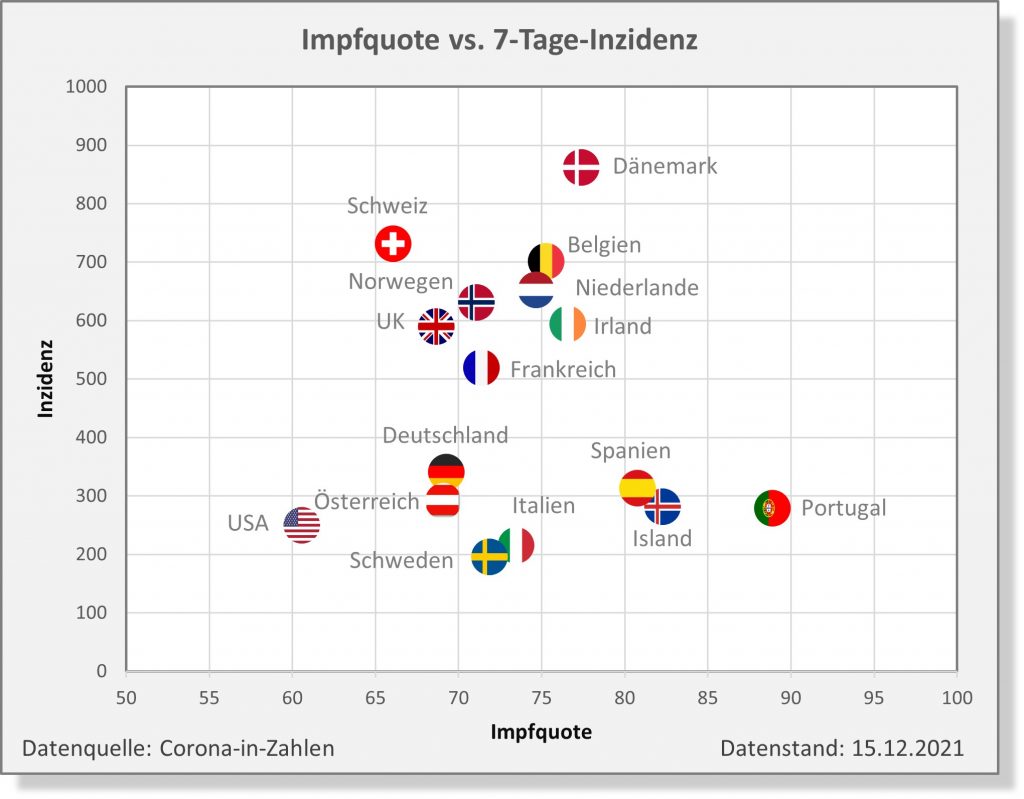
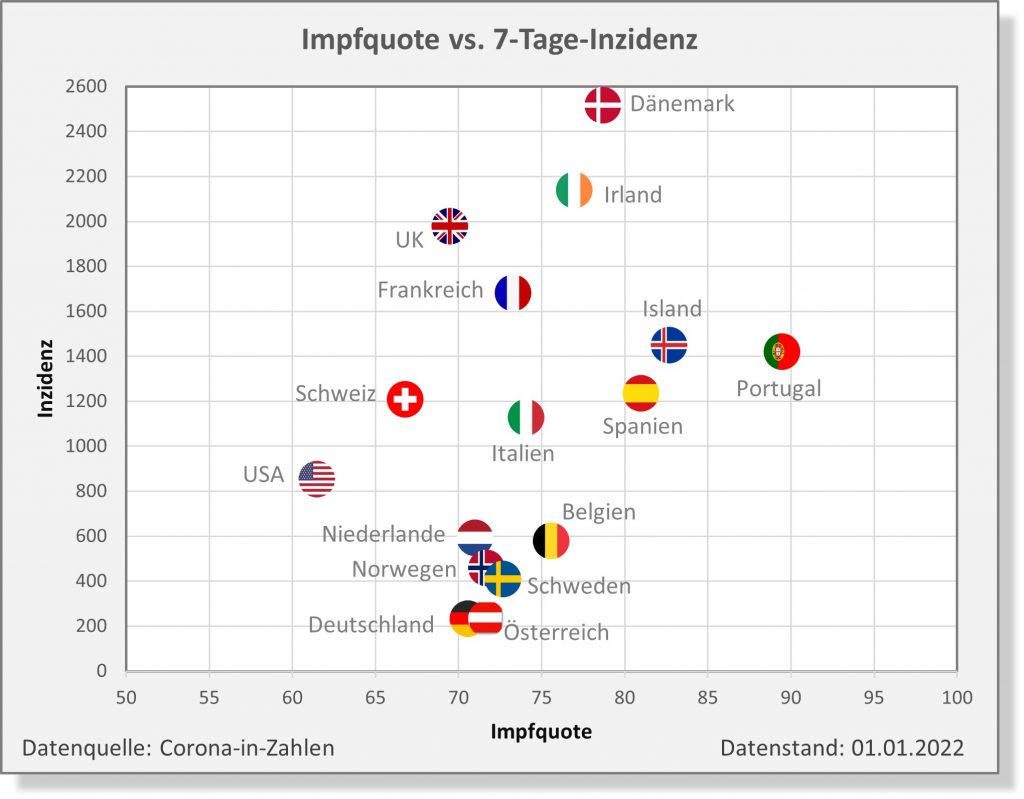
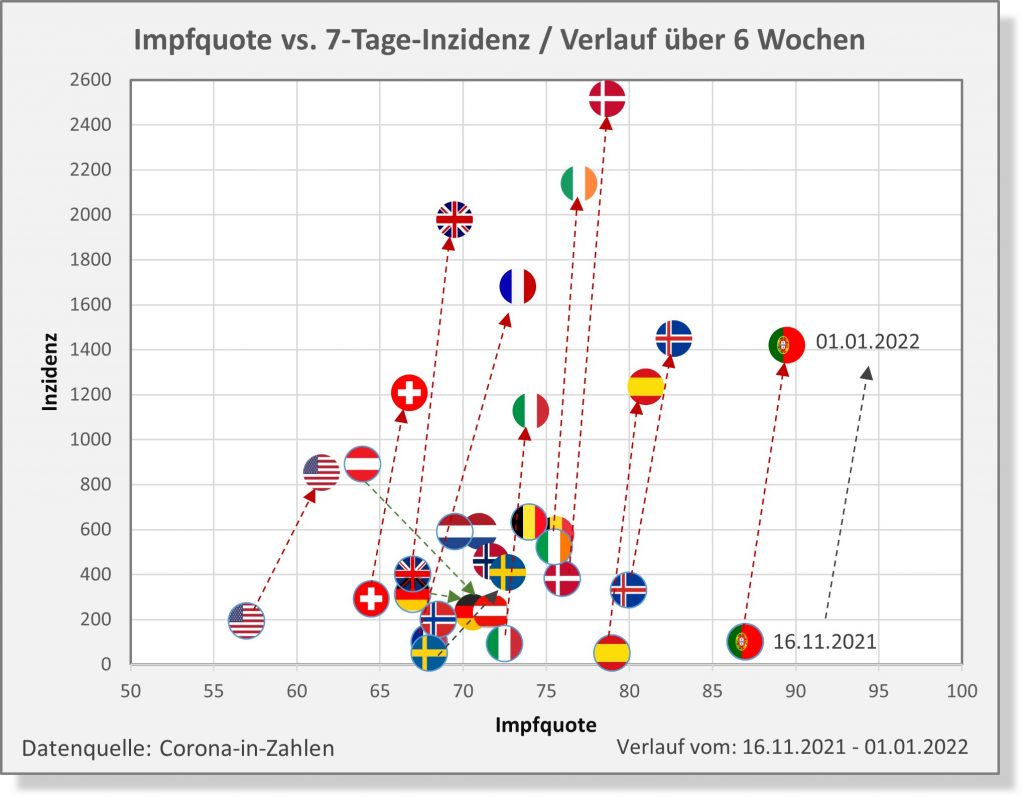
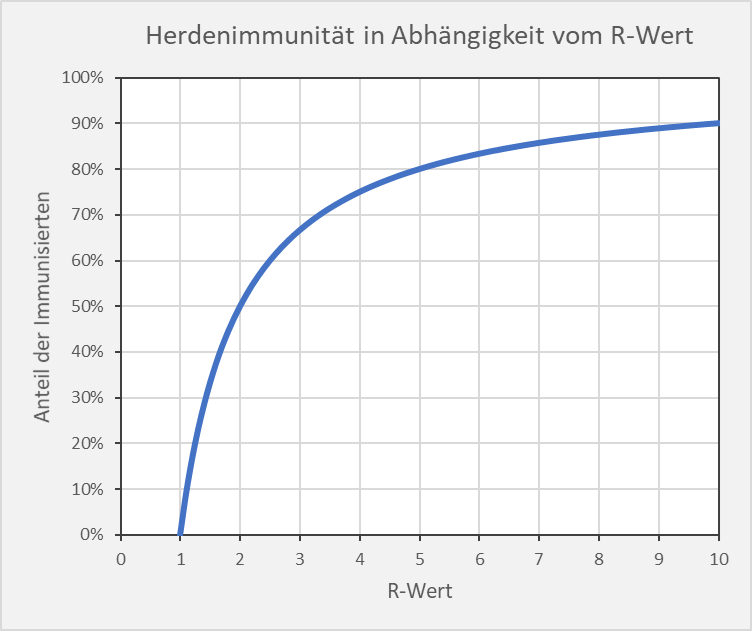
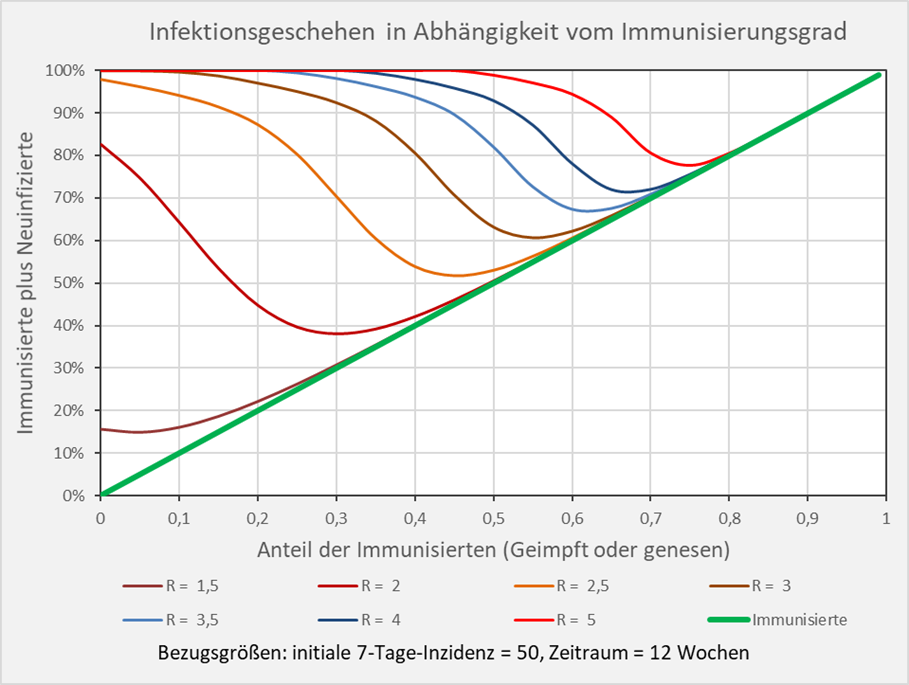
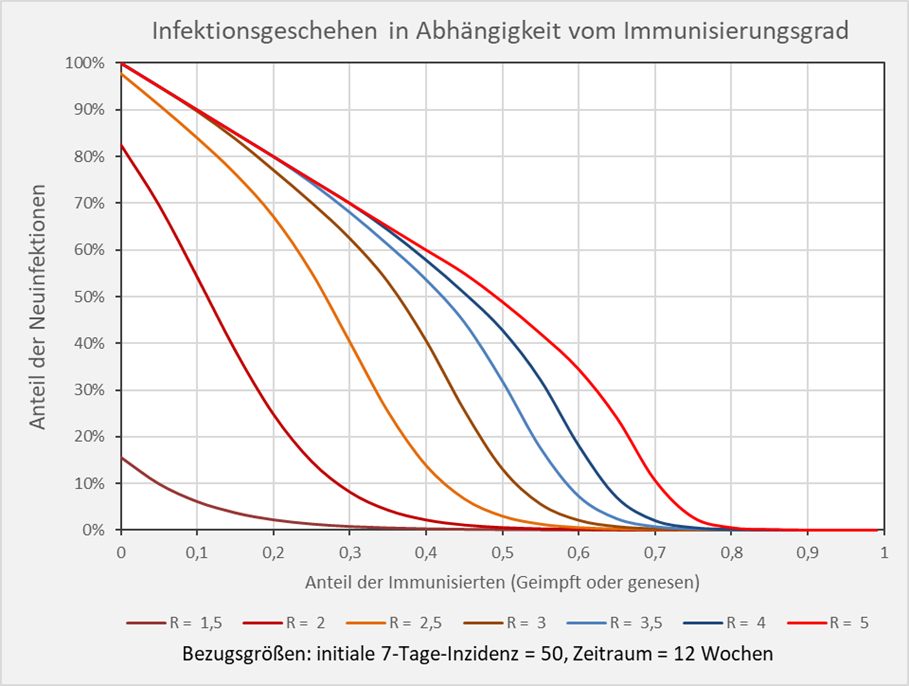
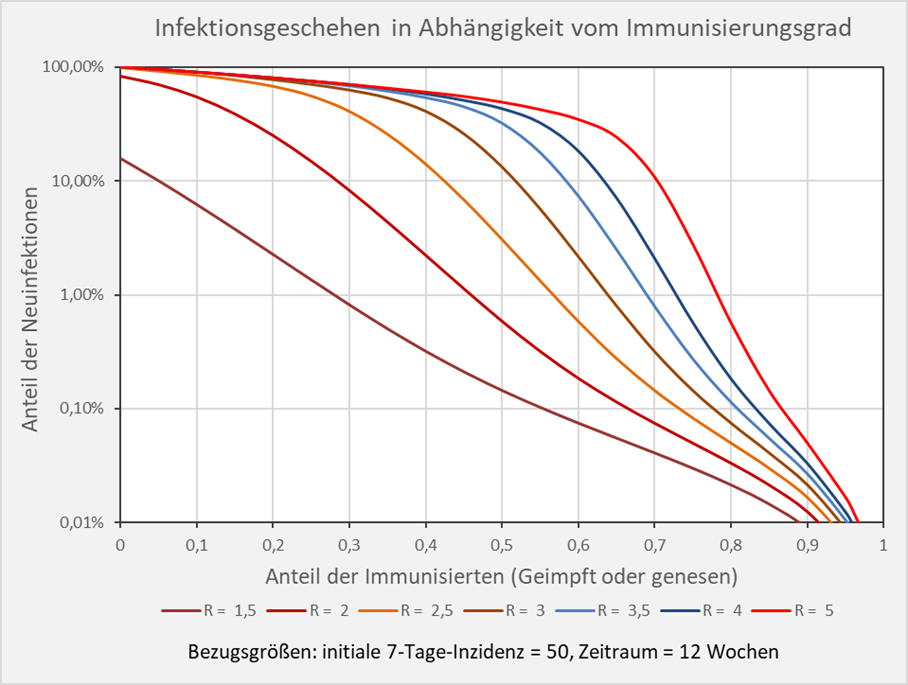
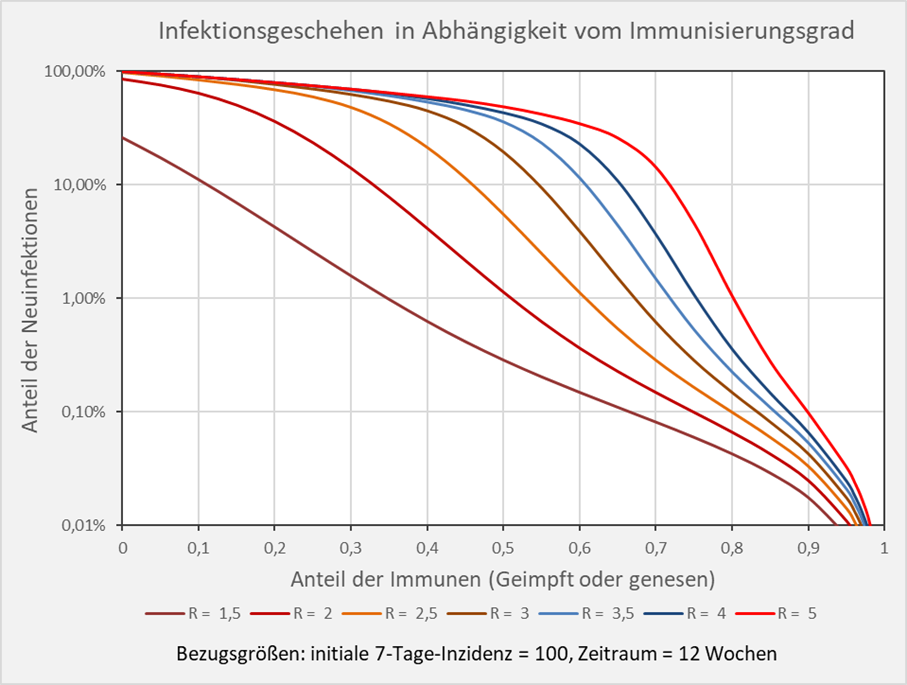
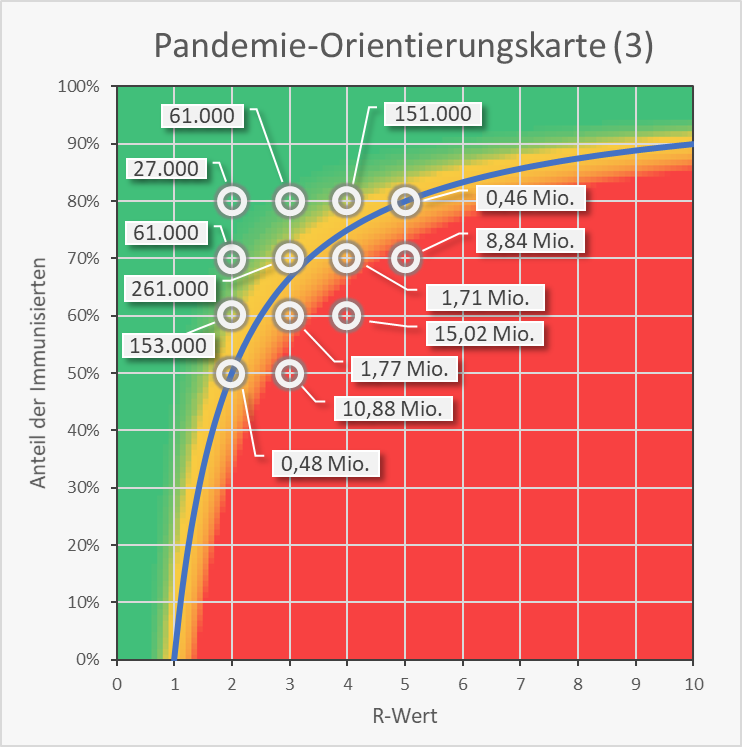
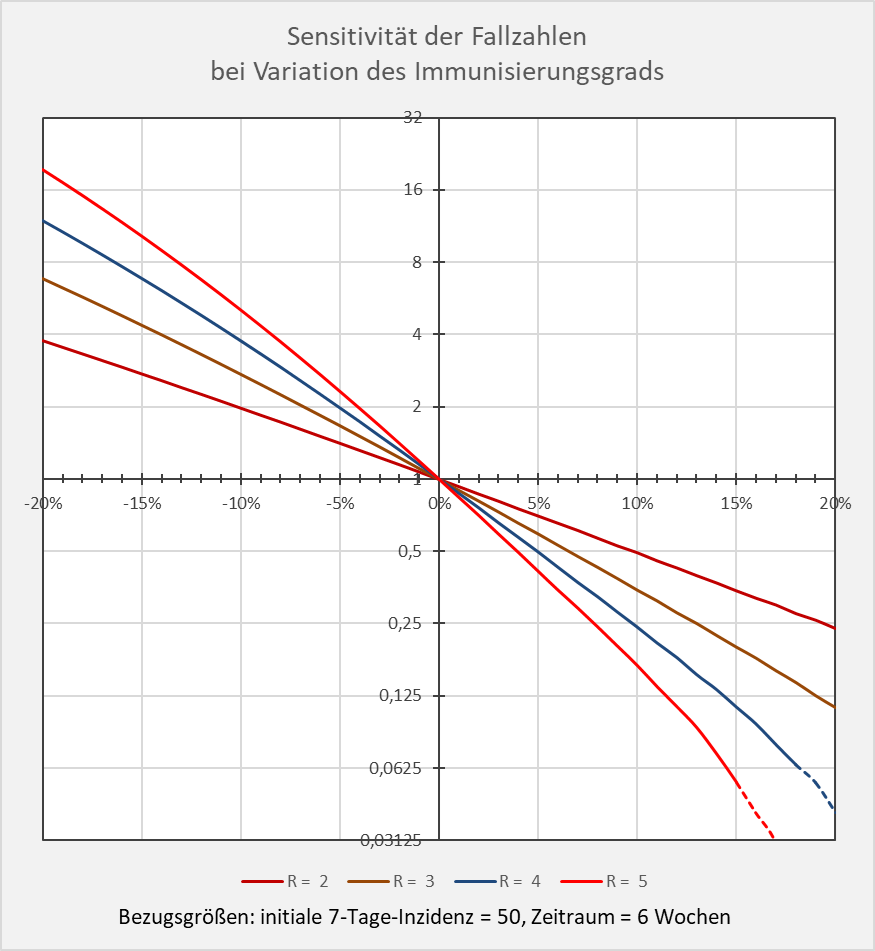
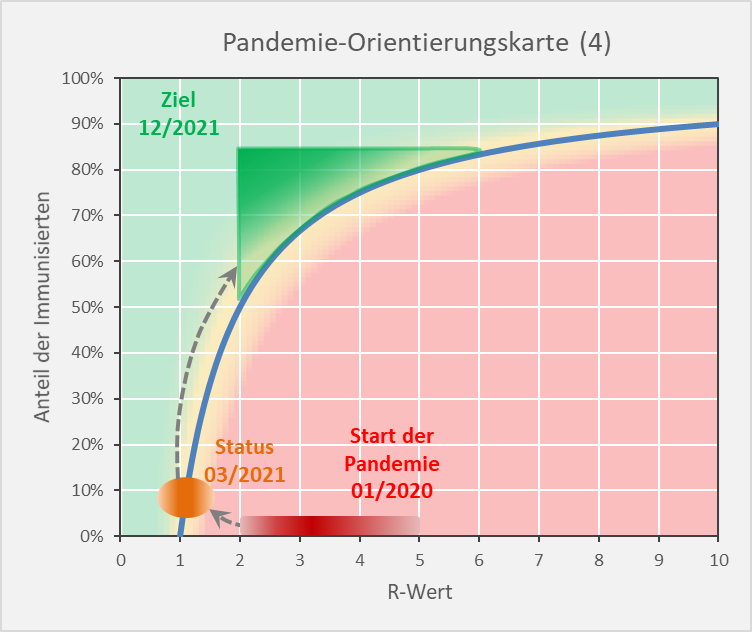
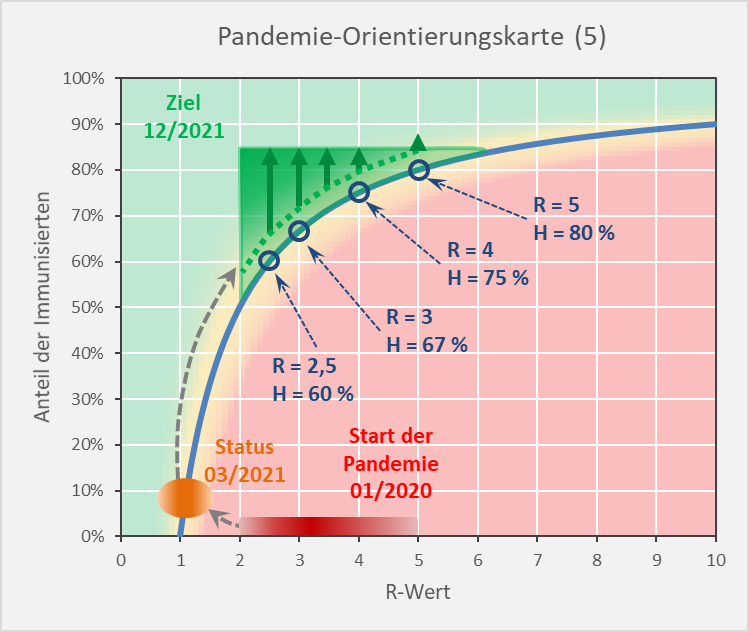
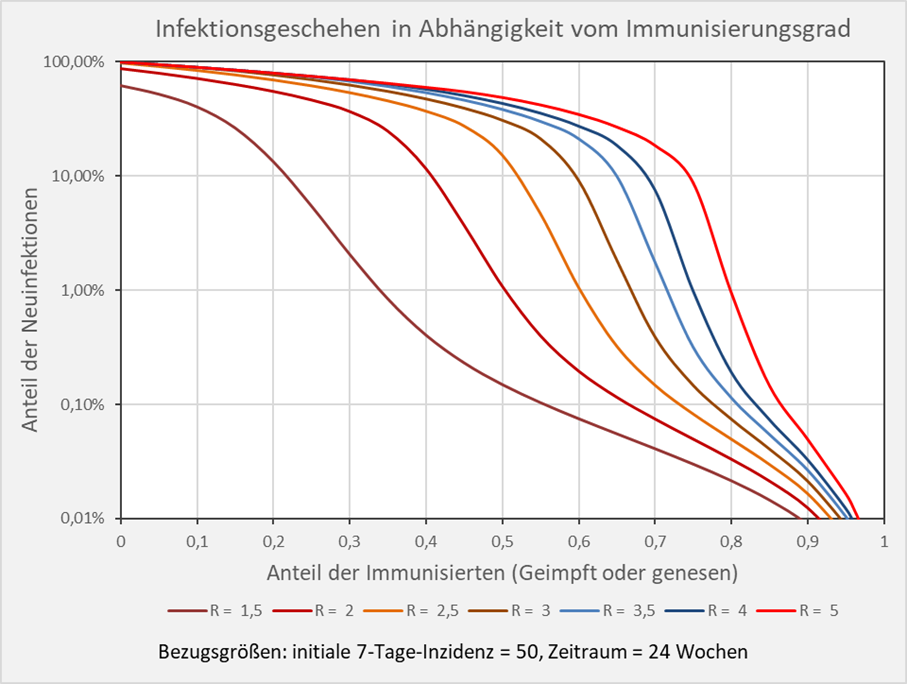
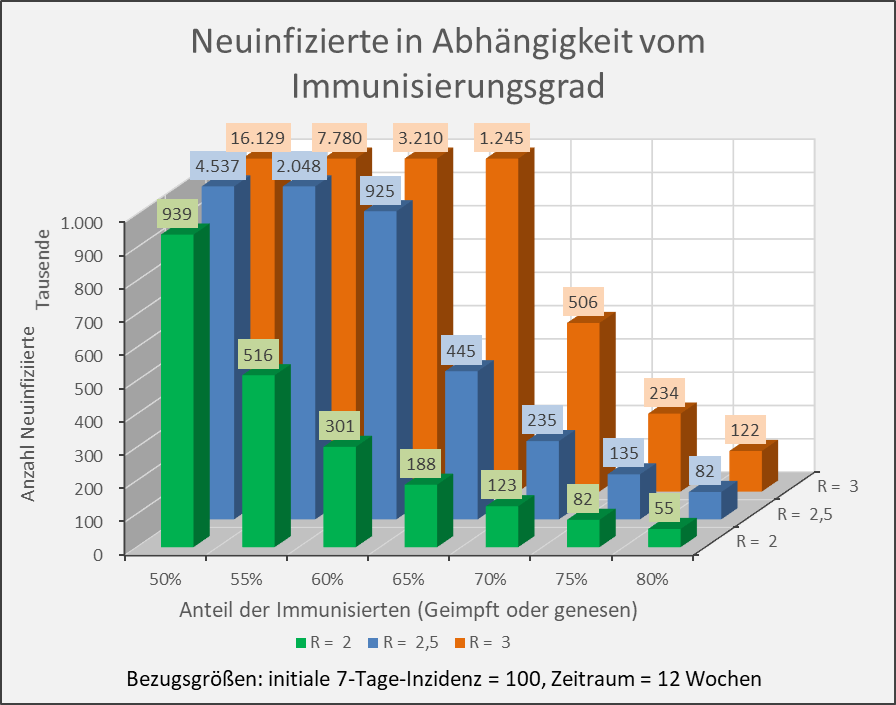
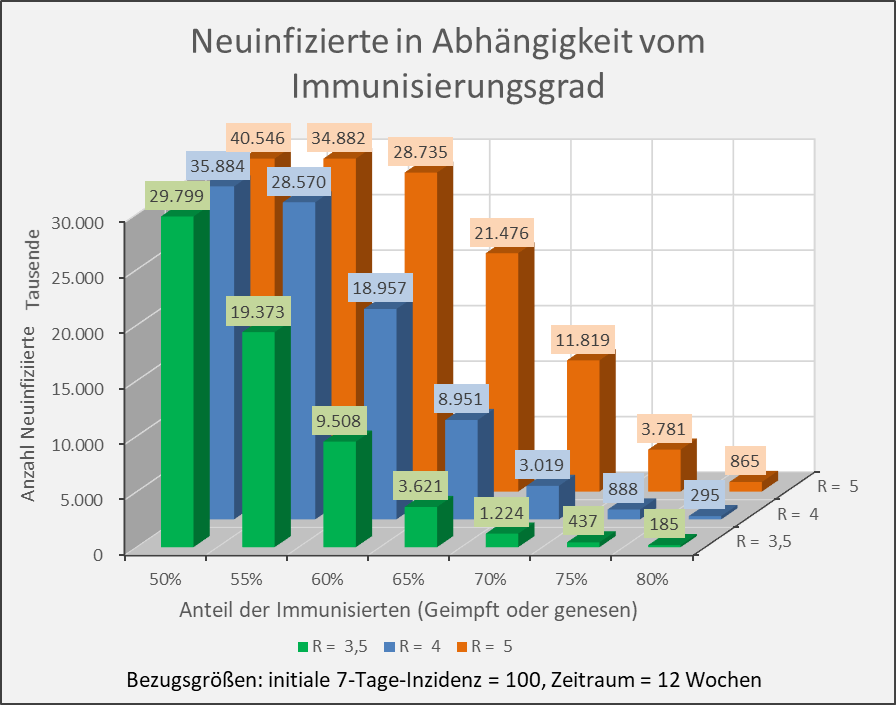
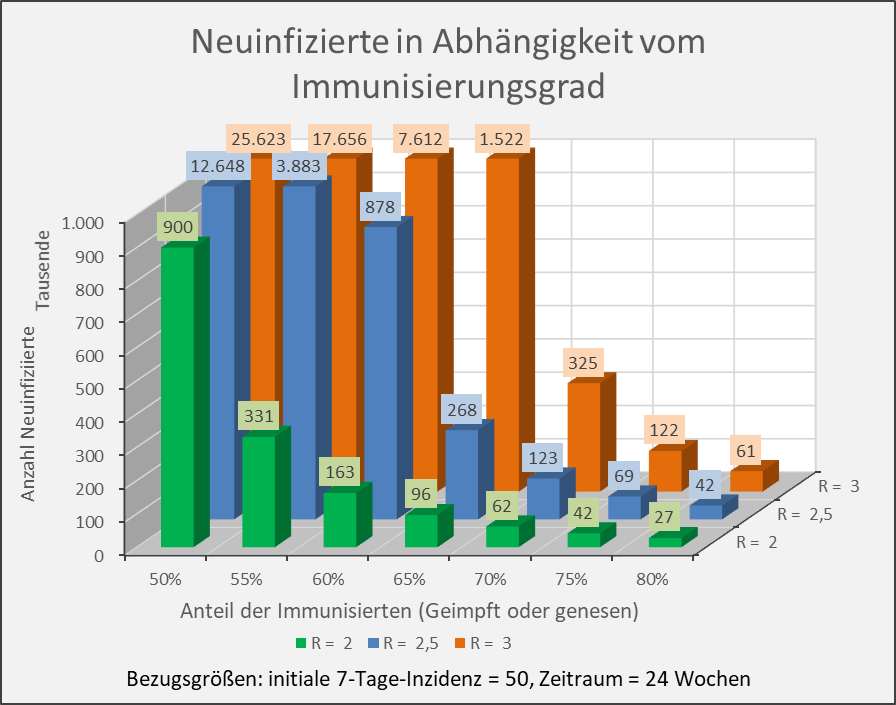
Dokumentierte Nebenwirkungen der Corona Impfung
In 2021 wurden in Deutschland ca. 150 Millionen Impfungen mit einem Corona-Impfstoff verabreicht. Insgesamt haben sich über 61 Mio. Personen impfen lassen. Die genauen Zahlen zu den Erst-, Zweit- und Drittimpfungen können Abb. 1 entnommen werden.
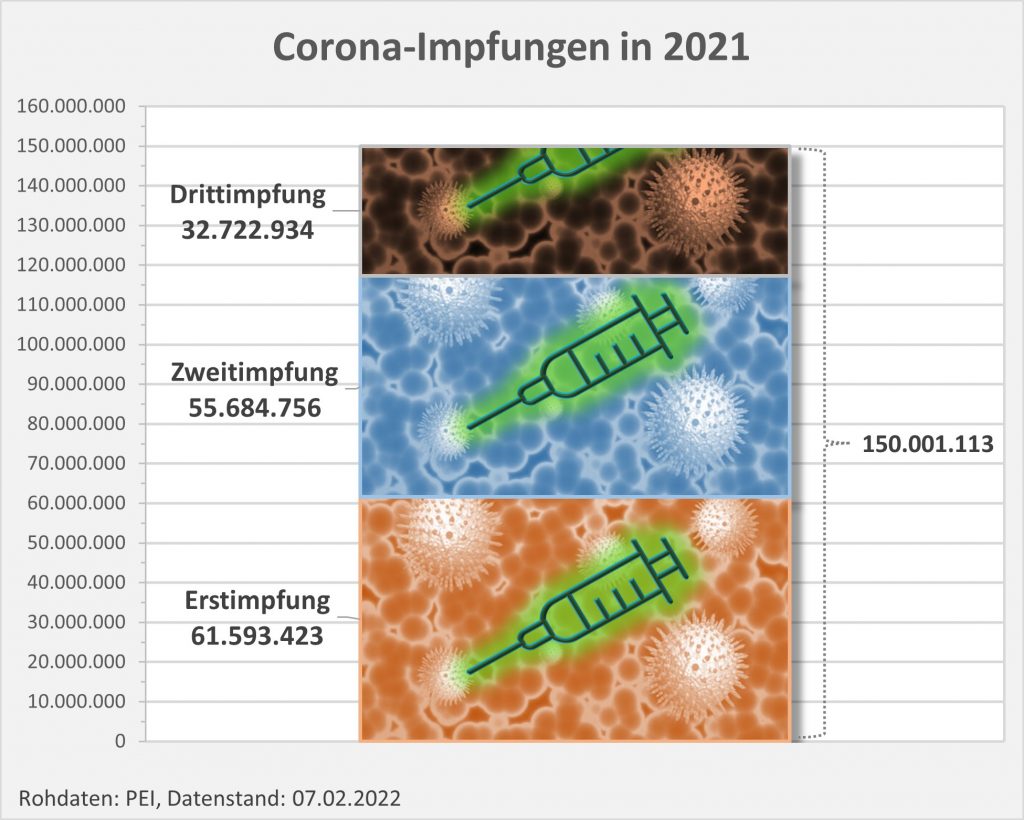
Abbildung 1: Anzahl der Impfungen. Rohdaten: PEI, Corona-Sicherheitsbericht 2021, Datenstand: 07.02.2022.
Ohne diese Impfungen hätte es wohl eine höhere Zahl von Corona-Todesfällen gegeben, vor allem bei den Älteren (s. [14]). Wo Licht ist, da ist aber auch Schatten: Laut Sicherheitsbericht des Paul-Ehrlich-Instituts (PEI, s. [1]) wurden im Zuge der Impfungen seit Beginn der Impfkampagne Ende 2020 insgesamt 244.576 Verdachtsfälle von Nebenwirkungen und Impfkomplikationen gemeldet (s. Abb. 2).
Viele dieser Meldungen beziehen sich auf letzten Endes vorübergehende Beeinträchtigungen. Betreffend die Dunkelziffer zu den nicht gemeldeten unmittelbaren Nebenwirkungen der Impfung weiß man natürlich nichts. Man kann aber davon ausgehen, dass leichtere Fälle wohl kaum Eingang in die offizielle Statistik finden.
In Summe kann man das abtun als statistische Pflichtübung: Was ist schon dabei, wenn die Einstichstelle für 1 oder 2 Tage schmerzt? Oder wenn man vorübergehend Kopfschmerzen hat? Tatsächlich reden wir hier In den meisten Fällen von temporären Beeinträchtigungen. In etwa 50 % der Fälle waren die Patienten wiederhergestellt oder ihr Allgemeinzustand war verbessert. Ganz so banal ist das dennoch nicht. Bei einem weiteren Drittel der Verdachtsfälle waren die Beeinträchtigungen zum Zeitpunkt der Meldung noch nicht abgeklungen. Und in immerhin 3 % der Fälle geht man von bleibenden Schäden aus.
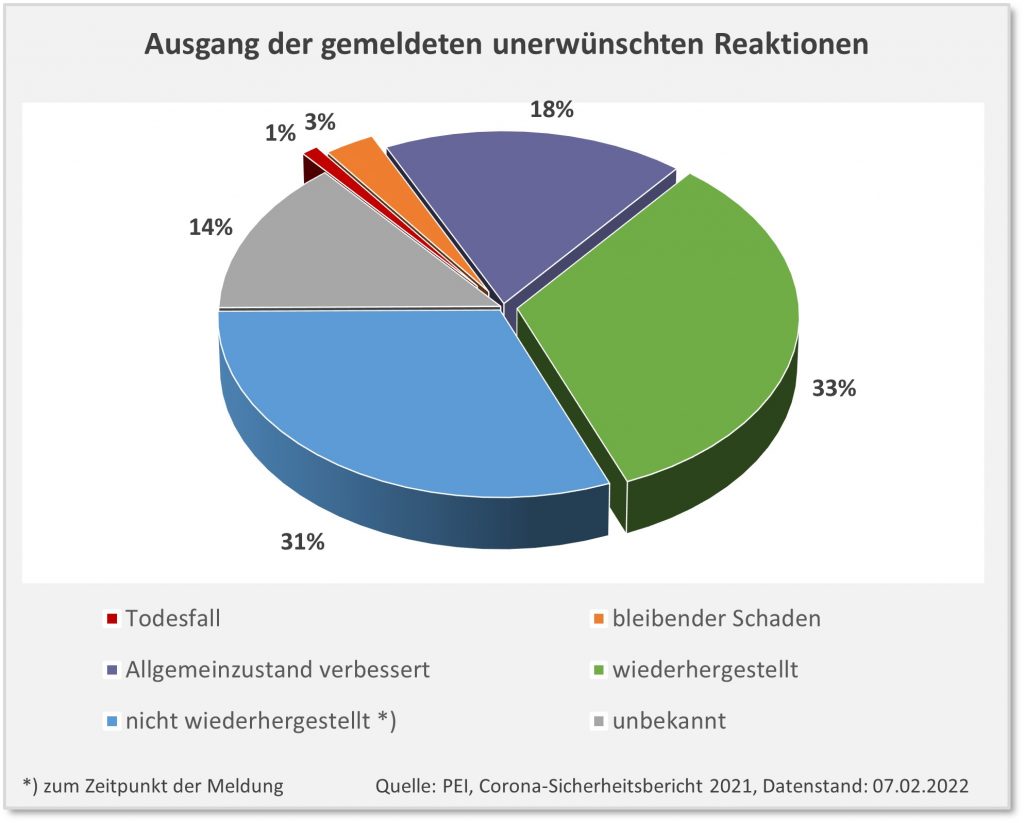
Abbildung 2: Ausgang der gemeldeten unerwünschten Reaktionen nach Impfung mit einem COVID-19-Impfstoff. Die Prozentangaben beziehen sich auf die Gesamtanzahl der gemeldeten Nebenwirkungen, d.h., 1 Prozentpunkt entspricht ca. 2.500 Fällen. Quelle: PEI, Corona-Sicherheitsbericht 2021, Datenstand: 07.02.2022.
Insgesamt gibt es eine erhebliche Zahl von 29.786 Verdachtsfällen bezüglich derer das PEI selbst von „schwerwiegenden“ unerwünschten Reaktionen spricht (s. Abb. 3). Darunter sind viele Geimpfte, die eine ambulante oder stationäre Behandlung benötigen. Und auch 2255 Verdachtsfälle mit tödlichem Ausgang werden verzeichnet.
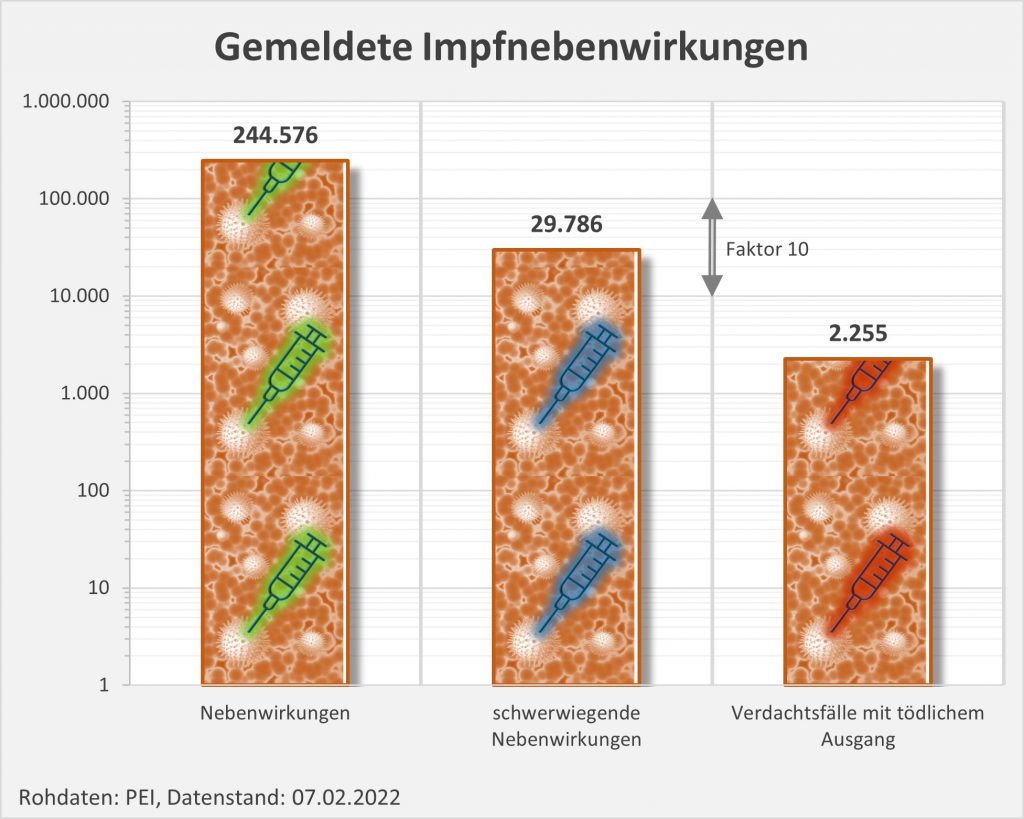
Abbildung 3: Anzahl der gemeldeten Nebenwirkungen, der schwerwiegenden Nebenwirkungen und der Verdachtsfälle mit tödlichem Ausgang. Man beachte die logarithmische Skalierung (kleine Werte erscheinen vergleichsweise groß). Rohdaten: PEI, Corona-Sicherheitsbericht 2021, Datenstand: 07.02.2022.
Natürlich muss man das alles in Relation zur Anzahl der Impfungen sehen. Dazu weiter unten.
Verdachtsfälle von Impftoten
Im Jahresbericht des PEI wird die Zahl von 2255 Meldungen mit einem tödlichen Ausgang „in unterschiedlichem zeitlichem Abstand zur Corona-Impfung“ genannt. Genaugenommen spricht das PEI hier von Verdachtsfällen. In 85 Einzelfällen, in denen Patienten an bekannten Impfrisiken wie Thrombose-mit-Thrombozytopenie-Syndrom (TTS), Blutungen aufgrund einer Immunthrombozytopenie oder Myokarditis im zeitlich plausiblen Abstand zur jeweiligen Impfung verstorben sind, hat das PEI den kausalen Zusammenhang mit der Impfung als möglich oder wahrscheinlich bewertet. Man fragt sich an dieser Stelle, was es mit den verbleibenden 2170 Verdachtsfällen auf sich hat. Dazu gibt es im Sicherheitsbericht lediglich einen statistischen Abgleich (s.u.). Es bleibt also offen, inwiefern hier eine ursächliche Beziehung zur Impfung bestehen könnte. Letztlich muss man daher auch in diesen Fällen die Kausalität der Impfung zumindest als „möglich“ erachten, es sei denn, dies kann im Einzelfall definitiv ausgeschlossen werden.
Meldungen über Impfkomplikationen an das PEI
Grundsätzlich werden Meldungen von Nebenwirkungen nach Impfung mit COVID-19-Impfstoffen über die Gesundheitsämter an das Paul-Ehrlich-Institut übermittelt. Ärzte sind gesetzlich verpflichtet, Impfkomplikationen, d. h. gesundheitliche Beschwerden, die über das übliche Ausmaß einer Impfreaktion hinausgehen und nicht evident auf andere Ursachen zurückzuführen sind, dem zuständigen Gesundheitsamt zu melden. Zusätzlich können auch Geimpfte bzw. deren Angehörige direkt dem Paul-Ehrlich-Institut melden.
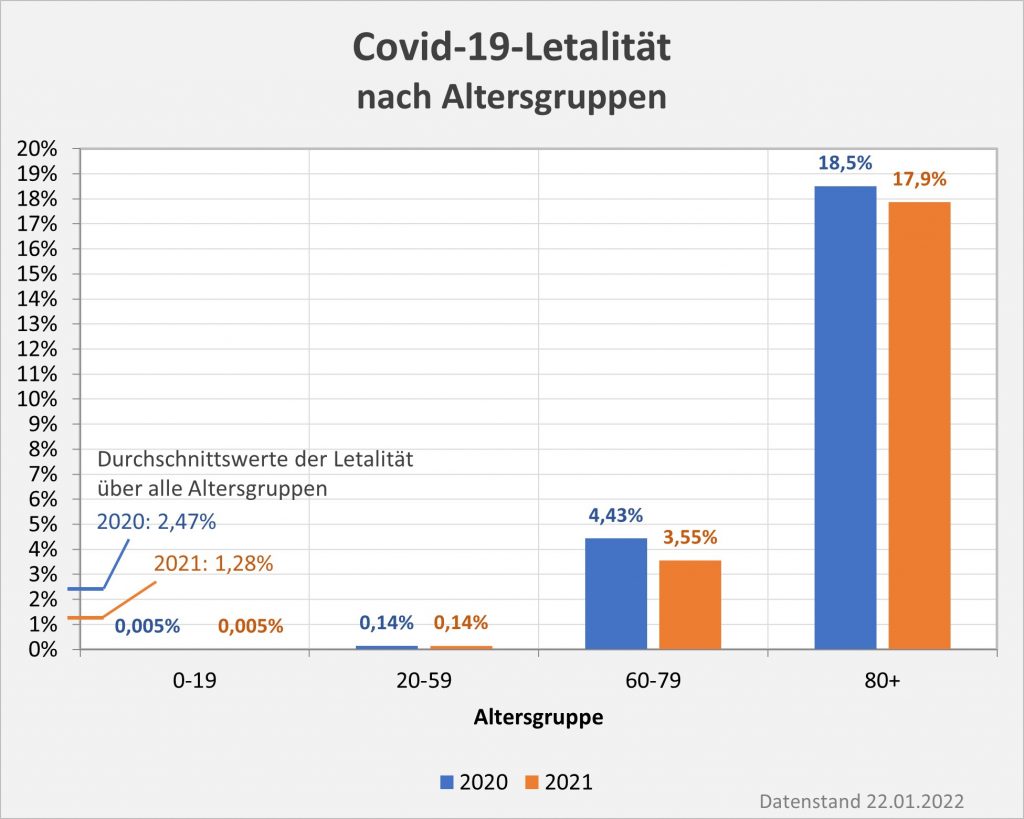
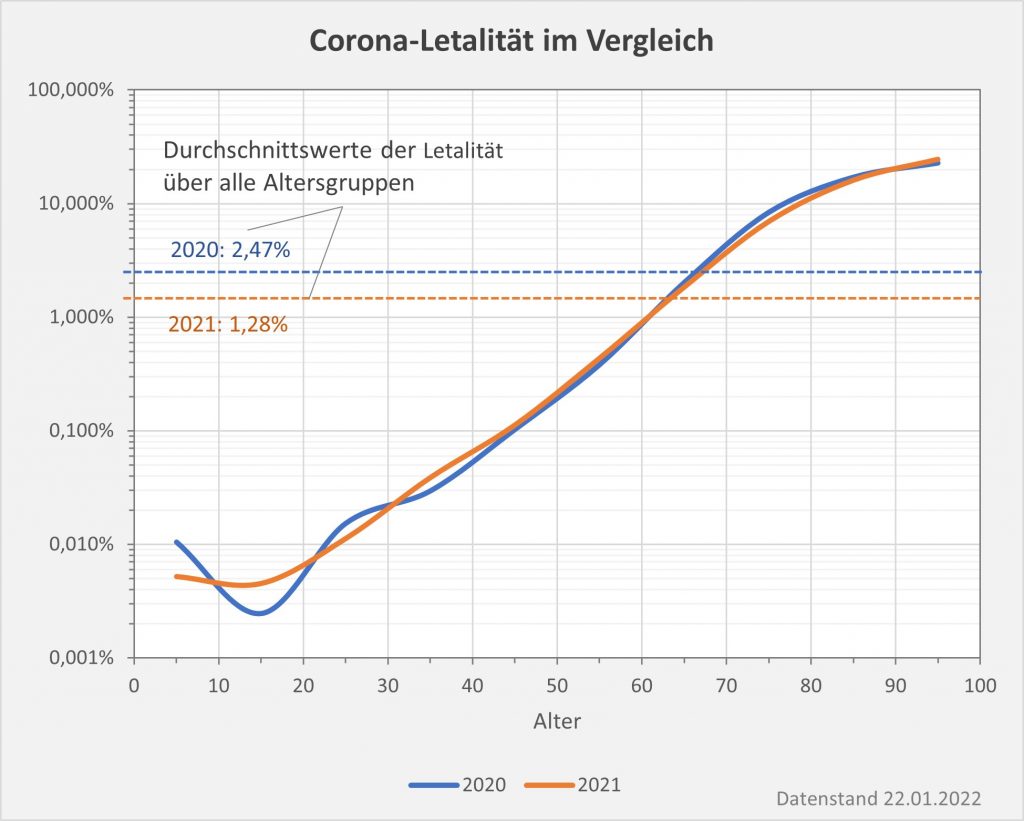
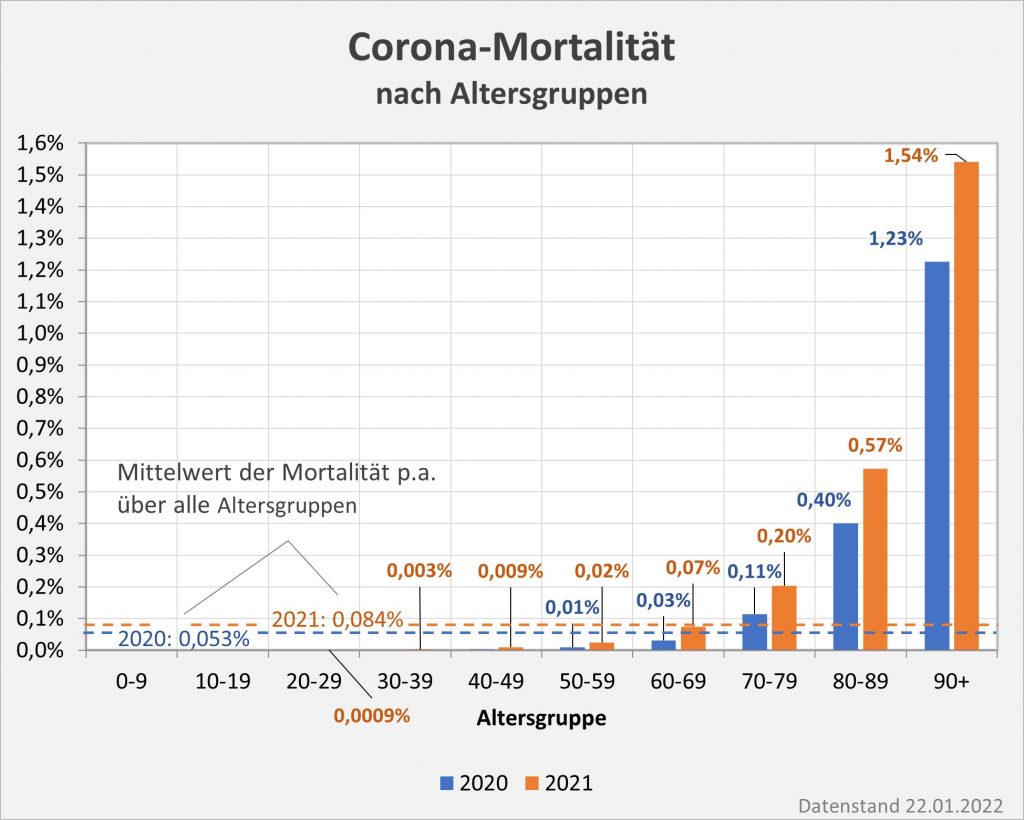
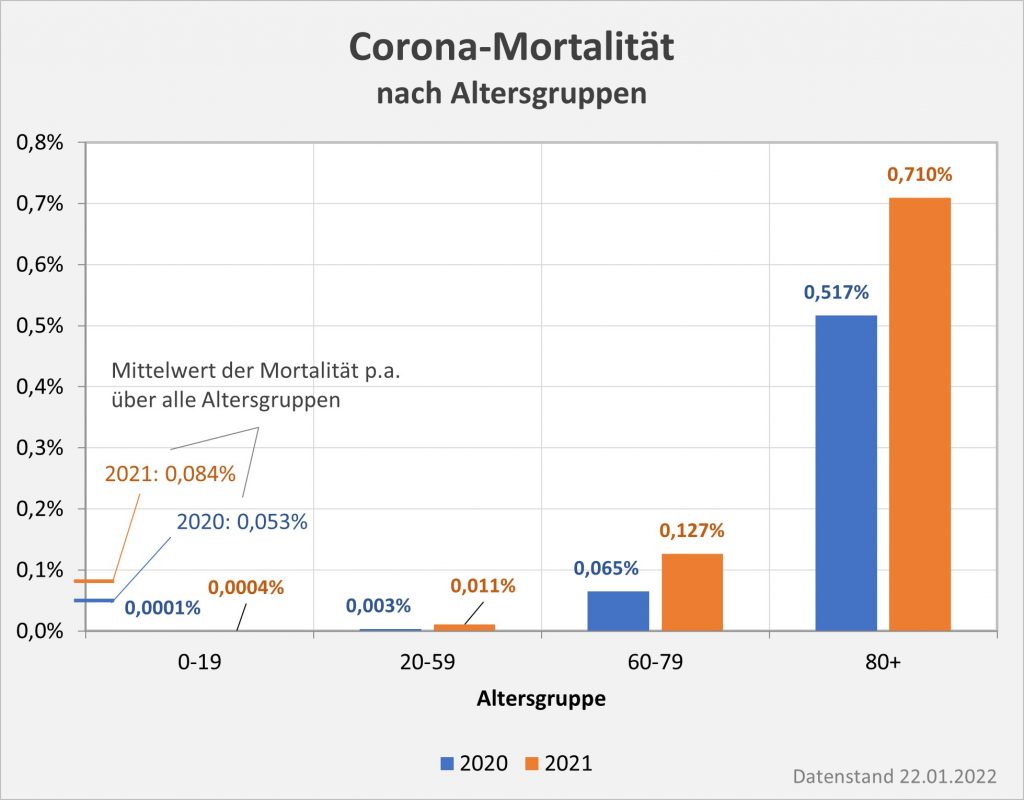
Kann man also davon ausgehen, dass die Mehrzahl der aufgetretenen Nebenwirkungen tatsächlich gemeldet werden? Nicht unbedingt! Bei den leichteren Fällen wird wohl oft eine Meldung unterbleiben. Jedenfalls ist das die Erfahrung von anderen Impfprogrammen. Man schätzt, dass i. A. nur in etwa 5 % der Fälle von Nebenwirkungen eine Meldung an das PEI erfolgt. Sofern es hier um leichtere Beeinträchtigungen geht, ist das nicht weiter von Belang und allenfalls von Interesse für die Statistik. Indessen kann man nicht ausschließen, dass auch schwerwiegende Fälle übersehen werden, z.B. dann, wenn das Auftreten von Krankheitssymptomen bei einer geimpften Person aufgrund von Vorerkrankungen oder aktuellen gesundheitlichen Beeinträchtigungen auch ohne die Impfung nicht völlig unerwartet gewesen wäre.
Nach einer aktuellen Analyse kommt die BKK Pro Vita zu einen ebenso ernüchternden wie alarmierenden Ergebnis: Es gebe viel häufiger Nebenwirkungen der Corona-Impfung als gedacht. Man gehe von einer sehr erheblichen Untererfassung aus. Die BKK rechnet vor, dass Nebenwirkungen der Impfung laut (ihren) Patientendaten mindestens zehn Mal häufiger sind als vom Paul-Ehrlich-Institut gemeldet. Wenn man die 10 Mio. Versicherte umfassende Stichprobe der BKK auf das Gesamtjahr und auf die Bevölkerung in Deutschland hochrechnet, sind vermutlich 2,5 bis 3 Millionen Menschen in Deutschland wegen Impfnebenwirkungen nach Corona-Impfung in ärztlicher Behandlung gewesen (s. [16]). Vier bis fünf Prozent (der Geimpften) waren wegen Nebenwirkungen beim Arzt.
Betrachten wir konkret das Szenario im Hinblick auf die Verdachtsfälle mit tödlichem Ausgang. Hier denkt man noch am ehesten, kein Fall könne unentdeckt bleiben. In Deutschland gibt es etwa 25.000 Hausarztpraxen. Von ihren Patienten sind circa 5 Millionen über achtzig. Zugleich ist die Impfquote in dieser Gruppe mit über 90 % sehr hoch. Im statistischen Mittel entfallen demnach jeweils 200 Über-80-Jährige auf eine Hausarztpraxis, und nahezu alle wurden 2021 geimpft. Die statistische Sterbewahrscheinlichkeit (völlig ohne Impfung) in dieser Altersgruppe liegt bei etwa 11,5 % p.a. Damit sind in 2021 pro Hausarztpraxis 23 Patienten über 80 verstorben, pro Monat also etwa 2 Personen. Es ist also absolut nicht ungewöhnlich, wenn von den 200 hochbetagten Patienten einer Hausarztpraxis jeden Monat 2 versterben. Ebenfalls nicht sonderlich überraschend ist es, wenn diese Sterbefälle innerhalb von 30 Tagen nach der Impfung auftreten: Es liegt ja völlig im Rahmen des Üblichen. Wenn nicht außergewöhnliche Umstände vorliegen, hat der Hausarzt kaum eine Chance, solche Todesfälle mit der Impfung in Zusammenhang zu bringen. Und was, wenn er davon gar nichts erfährt, weil sich der Patient im Impfzentrum hat impfen lassen?
Die Meldungsstatistik des PEI ist daher zunächst einmal nur eine Grundlage für die grobe Beurteilung von Risiken. Eine abschließende Bewertung ist auf dieser Basis kaum möglich (s. a. [16]).
Risikoeinschätzung auf Basis der Meldezahlen
Das PEI bezieht die gemeldeten Fälle auf die Anzahl der Impfdosen. Das erscheint naheliegend und zweckmäßig. In Relation zu den ca. 150 Mio. Impfungen ergibt sich auf dieser Basis eine Melderate von 1600 Fällen von Nebenwirkungen pro 1 Mio. Impfungen, und 200 Fällen von schwerwiegenden Nebenwirkungen pro 1 Mio. Impfungen. Der relative Anteil der Verdachtsfälle mit tödlichem Ausgang liegt bei 15 pro 1 Mio. Impfungen. Um zu einer ersten Einschätzung zu kommen, inwiefern das viel oder wenig ist, kann man diese Zahl den im gleichen Zeitraum „an oder mit“-Corona-Verstorbenen gegenüberstellen. Aufgrund der knapp 70.000 Coronatoten in 2021 sind das etwa 839 Tote pro 1 Mio. Einwohner, mithin etwa das 56-fache der Anzahl der Verdachtsfälle von Impftoten. Doch ist dieser Vergleich zulässig?
Für die Risikoeinschätzung sinnvoller erscheint die Bezugnahme auf die Anzahl der Geimpften. Letzten Endes muss doch die mögliche Gefährdung der Person interessieren, nicht das Risiko des impfenden Arztes. Wenn man sich, wie das PEI, auf die Anzahl der Impfungen bezieht, wird das Bild in unzulässiger Weise geschönt insofern das Risiko kleiner erscheint als es wirklich ist.
Die o.g. ca. 150 Mio. Impfdosen wurden lt. PEI an 61.593.423 Personen verabreicht. Im Mittel wurde demnach jeder Geimpfte etwa zweieinhalbmal „gepikst“. Berücksichtigt man dies in der Statistik, so ergibt sich ein geschärftes Bild zum Risiko:
- 3971 Fälle von Nebenwirkungen pro 1 Mio. Geimpfte
- 484 Fälle von schwerwiegenden Nebenwirkungen pro 1 Mio. Geimpfte
- 37 Verdachtsfälle mit tödlichem Ausgang pro 1 Mio. Geimpfte
Vergleicht man die letzte Zahl wieder mit den 839 Coronatoten pro 1 Mio. Einwohner, so ergibt sich nun ein Verhältnis von 23:1. Das spricht im Grundsatz immer noch klar für die Impfung, das Risikoverhältnis ist aber nicht so überwältigend positiv, wie man das eigentlich vermuten würde. Vor allem, wenn man dabei die völlig unterschiedliche Corona-Risikobewertung im Hinblick auf die diversen Altersgruppen berücksichtigt
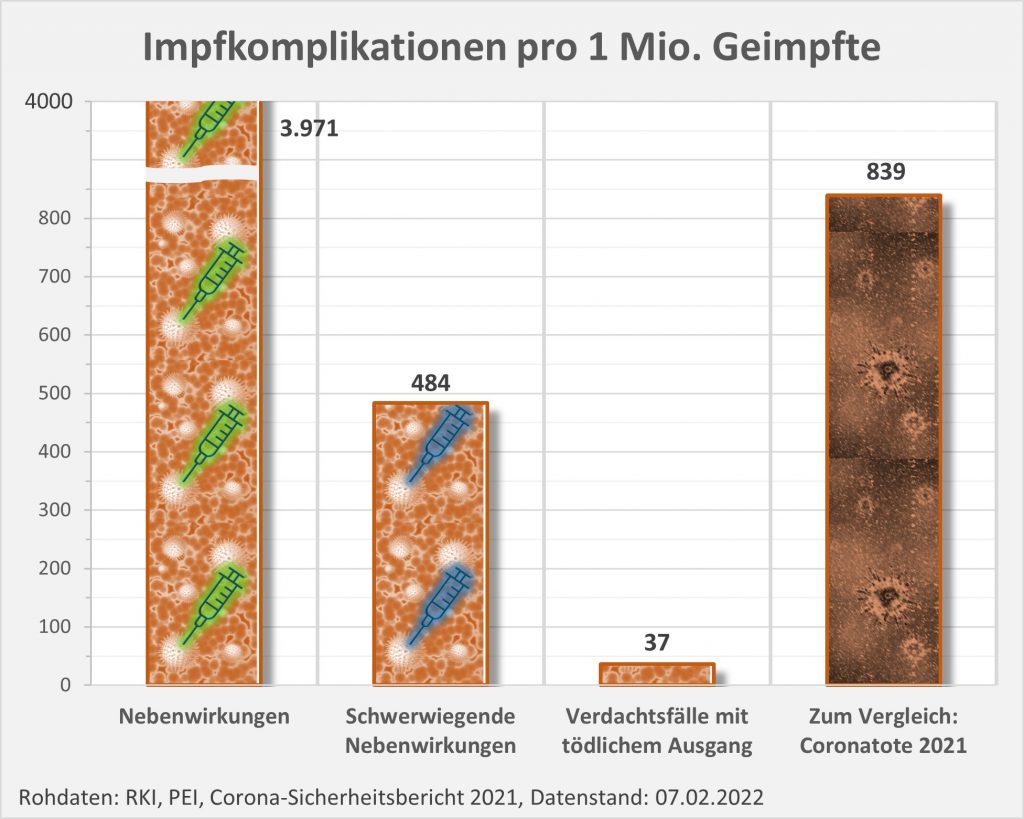
Abbildung 4: Melderate über Verdachtsfälle von Nebenwirkungen und Impfkomplikationen nach Impfung zum Schutz vor COVID-19 pro 1 Mio. Geimpfte seit Beginn der Impfkampagne am 27.12.2020 bis zum 31.12.2021. Zum Vergleich ist in der rechten Rubrik die Corona-Todesfallzahl pro 1 Mio. Einwohner eingetragen. Rohdaten: RKI, PEI, Corona-Sicherheitsbericht 2021, Datenstand: 07.02.2022.
Die Anzahl der gemeldeten schwerwiegenden Nebenwirkungen liegt „nur“ 58 % unter der Anzahl der registrierten Todesfälle „an oder mit“ Corona. Das ist ein vergleichsweise kleiner Abstand. Wobei trotzdem klar ist: Vor die Wahl gestellt, würden sicher alle Verstorbenen die Alternative der schwerwiegenden Nebenwirkung nach der Impfung gerne in Kauf genommen haben.
Zusammenhang zwischen Impfung und möglichen Nebenwirkungen
Aufgrund der Meldungssystematik darf man zweifelsohne unterstellen, dass zumindest die zeitnah auftretenden Nebenwirkungen zu einem gewissen Teil erfasst werden. Selbst wenn wir davon ausgehen, dass es gar keine Dunkelziffer gibt, wird man die Fallzahl mit knapp 250.000 Fällen von Nebenwirkungen und knapp 30.000 Verdachtsfällen von schwerwiegenden unerwünschten Reaktionen kaum als vernachlässigbar abtun können. Es sind fraglos viele Fälle. In Relation zu den ca. 150 Mio. Impfungen ist die Melderate aber dennoch klein: 1,6 Fälle von Nebenwirkungen pro 1000 Impfungen, und 0,2 Fälle von schwerwiegenden Nebenwirkungen pro 1000 Impfungen.
Dabei hat man es hier im Grundsatz mit einfach zu identifizierenden Impfreaktionen zu tun, weil sie in einem engen zeitlichen Abstand zur Impfung auftreten. Viel schwieriger oder gar unmöglich ist der Nachweis einer nachgelagerten Folgewirkung, die erst Monate oder gar Jahre nach der Impfung auftritt. Wie wollte man denn zweifelsfrei belegen, dass das Auftreten einer Autoimmunkrankheit auf eine Jahre zurückliegende Impfung zurückzuführen sei? Allenfalls würde man in diesem Falle eine statistische Korrelation finden können, was natürlich kein Beweis ist. Vor Gericht hätte ein solcher Nachweis wohl kaum Bestand.
Laut PEI ist von langfristigen Impffolgen nichts bekannt. Darf man daraus schließen, dass es solche Impffolgen nicht gibt? Diese Schlussfolgerung ist möglicherweise übereilt. Das Wirkprinzip von mRNA-Impfstoffen ist neu, deswegen kann man auch nachgelagerte oder indirekte Folgen auf das Immunsystem nicht mit Sicherheit ausschließen. Wer dies tut, verstößt gegen elementare wissenschaftliche Prinzipien und handelt unredlich. Analogieschlüsse aus den historischen Impfprogrammen sind nicht hinreichend für den Ausschluss von Langzeitfolgen, weil die Analogie aufgrund des neuartigen Wirkprinzips so nicht besteht.
Man muss sich vergegenwärtigen, dass die mRNA-Impfstoffe noch immer nicht über eine reguläre Zulassung verfügen. Von der Politik und den Medien wird das weitgehend ignoriert. Stattdessen verweist man gerne auf das Paul-Ehrlich-Institut und präsentiert meistens solche Wissenschaftler, die in ihren Statements jegliche von der Impfung möglicherweise ausgehenden Gefährdungen mehr oder weniger als Hirngespinste abtun. Indessen gibt es aber auch seriöse kritische Stimmen, auch wenn man wenig von ihnen hört (s. dazu [17] Fragezeichen beim mRNA-Impfstoff).
Auch wenn man eine unmittelbare Gefahr mit größter Sicherheit ausschließen kann, da die Impfstoffe schon millionenfach verabreicht wurden (darauf fußt das Urteil des PEI), so gebietet die wissenschaftliche Skepsis im Verein mit der ärztlichen Vorsicht, solche vorschnellen Verharmlosungen zu unterlassen. Dies vor allem dann, wenn es um Impfprogramme für Kinder geht. Es besteht ein Restrisiko, über das man nichts Genaues weiß. Möglicherweise wird es sich als klein erweisen, das ist aber nicht gewiss. Wer das Risiko jetzt aus politischen Gründen kleinredet, ignoriert eherne wissenschaftliche Grundsätze und wird seiner Verantwortung nicht gerecht.
Natürlich kann man pragmatisch argumentieren, das bekannte von Corona ausgehende Risiko sei höher einzuschätzen als das unbekannte Restrisiko möglicher Spätfolgen. Das ist ein politisch opportuner Zugang, den man durchaus vertreten kann. Man muss ihn aber nicht zwingend gutheißen, weil ihm die wissenschaftliche Grundlage fehlt. Zumindest sollte, wer dies propagiert, sich nicht auf die Wissenschaft berufen. Es ist dennoch ein oft anzutreffendes Verhalten: Risiken, die man in Ermangelung verlässlicher Daten und gezielter Untersuchungen nicht quantifizieren kann, werden kurzerhand als nicht existent deklariert. Manchmal wird das sogar explizit als „wissenschaftlich“ ausgegeben, sogar von Wissenschaftlern – tatsächlich ist es nicht mehr als Augenwischerei.
Jedenfalls ist es unwissenschaftlich und damit unseriös, mögliche Langzeitfolgen pauschal auszuschließen. Diesen Schluss mögen sich Leute zutrauen, die ihr Wissen durch den Blick in die Kristallkugel gewinnen.
Zusammenhang zwischen Impfung und möglichen Todesfällen
Kann man davon ausgehen, dass zumindest die Verdachtsfälle mit tödlichem Ausgang nach der Impfung vollständig erfasst werden? Daran muss man Zweifel anmelden. Die Gründe dafür liegen wieder in der Statistik.
Unabhängig von der Impfung liegt die durchschnittliche Sterblichkeit bei 1,24 % p.a. Von einer Million Menschen sterben also statistisch gesehen 12.400 innerhalb der nächsten 12 Monate nach einem willkürlich festgesetzten Datum. Entsprechend sterben nach der verabreichten Impfung im statistischen Mittel ca. 1000 Personen im Laufe der folgenden 30 Tage. Hochgerechnet auf die Gesamtanzahl der in 2021 Geimpften (61,5 Mio.) muss man daher 61.500 Tote innerhalb von gut 4 Wochen nach der Impfung erwarten. Tatsächlich wurden aber nur 2255 Todesfälle (3,7 % von 61.500) in zeitlicher Nähe zur Impfung registriert. Was kann man daraus schließen?
Dreierlei:
- Nur ein Bruchteil von weniger als 4 % der statistisch zu erwartenden Verdachtsfälle mit tödlichem Ausgang innerhalb von 4 Wochen nach der Impfung wurde tatsächlich gemeldet (Meldequote 1 Fall von 27). Das könnte darauf hindeuten, dass der mögliche Zusammenhang zwischen Impfung und Versterben in vielen Fällen nicht registriert wurde (s. dazu auch obiges Beispiel betreffend der Hausarztpraxen).
- Wenn wir unterstellen, dass jeder dieser Todesfälle im Hinblick auf die Impfung ärztlich bewertet wurde, dann würde sich damit der Verdacht der Impfkausalität erhärten. Wir müssten also davon ausgehen, dass in all diesen Fällen (also den genannten 2255) der Tod mit hoher Wahrscheinlichkeit als unmittelbare Folge der Impfung eingetreten ist. Damit wären das keine bloßen Verdachtsfälle mehr.
- Es gibt noch eine dritte Sicht: Die nur etwa 4 % dokumentierten Verdachtsfälle liegen im Bereich der möglichen statistischen Schwankungen und fallen daher in der Gesamtschau nicht ins Gewicht. Die Gesamtanzahl der Verstorbenen ist aufgrund der Impfung offensichtlich nicht statistisch signifikant angestiegen. Daraus kann man unmittelbar auf die relative Harmlosigkeit der Impfung schließen. Das ist in etwa die Position des PEI.
Was ist zutreffend? Man darf vermuten, dass alle drei Sichten einen Teil der Wahrheit repräsentieren. Die nackte Statistik spricht für die Position des PEI. Wenn vom Impfstoff tatsächlich eine nennenswerte Gefahr in unmittelbarer zeitlicher Nähe zur Impfung ausgehen würde, dann müsste sich das in den Todesfallzahlen zeigen. Dass dies dennoch eine Gratwanderung ist, zeigt die folgende Überlegung: Vorausgesetzt, wir zählen nur die unmittelbar nach der Impfung und ggf. am Folgetag aufgetretenen Todesfälle, dann ergeben sich dafür im statistischen Mittel 2050 Tote (= 61.500/30). Das sind in etwa bereits so viele, wie insgesamt für das gesamte Jahr an das PEI gemeldet wurden. Diese Fallzahl würde man auch dann erwarten, wenn man ein Placebo gespritzt hätte. Es erscheint daher zweifelhaft, inwiefern mittels dieser Vorgehensweise eine schwach ausgeprägte Todeskausalität überhaupt identifiziert werden könnte.
Umgekehrt kann man sich auch fragen, bei welcher Anzahl von Verdachtsfällen ein mögliches Risiko erkannt werden würde. Die 2255 Fälle werden offenbar noch nicht als Risikosignal gesehen, da sie mehr oder weniger im statistischen Rauschen untergehen. Indessen würden auch 10.000 Verdachtsfälle noch weit unter der statistisch zu erwartenden Anzahl von 61.500 Fällen liegen. Es ist daher eine offene Frage, inwieweit dieser Ansatz überhaupt dafür geeignet ist, mögliche Risiken sicher zu erkennen. Um es ganz pointiert zum Ausdruck zu bringen: Wenn die Menschen nach der Impfung nicht wie die Fliegen sterben, dann wird man mittels dieser Methodik kaum valide Indizien für eine eventuell bestehende ernsthafte Problematik finden.
Betreffend möglicher Langzeitfolgen ist die Situation keineswegs besser: Es gibt derzeit kein Verfahren für die sichere Detektion möglicher Risikofaktoren.
Vergleich mit anderen Impfprogrammen
Von 2000 bis 2019 wurden in Deutschland mehr als 580 Mio. Impfungen durchgeführt, im Schnitt also immerhin mindestens 34 Mio. Impfungen pro Jahr. Dabei waren insgesamt 456 Todesfälle nach Impfungen gemeldet worden (jährlich also etwa 22 Fälle). Im Vergleich dazu fallen die 2255 Verdachtsfälle mit tödlichem Ausgang in 2021 aus dem Rahmen (s. Abb. 5). Und zwar erheblich: Für ein Viertel der verabreichten Impfdosen zählen wir die fünffache Anzahl von Verdachtsfällen mit tödlichem Ausgang. Im Ergebnis ist damit das potentiell von der Corona-Impfung ausgehende Risiko etwa zwanzigmal höher als das mittlere Risiko in den historischen Impfprogrammen der letzten 20 Jahre.
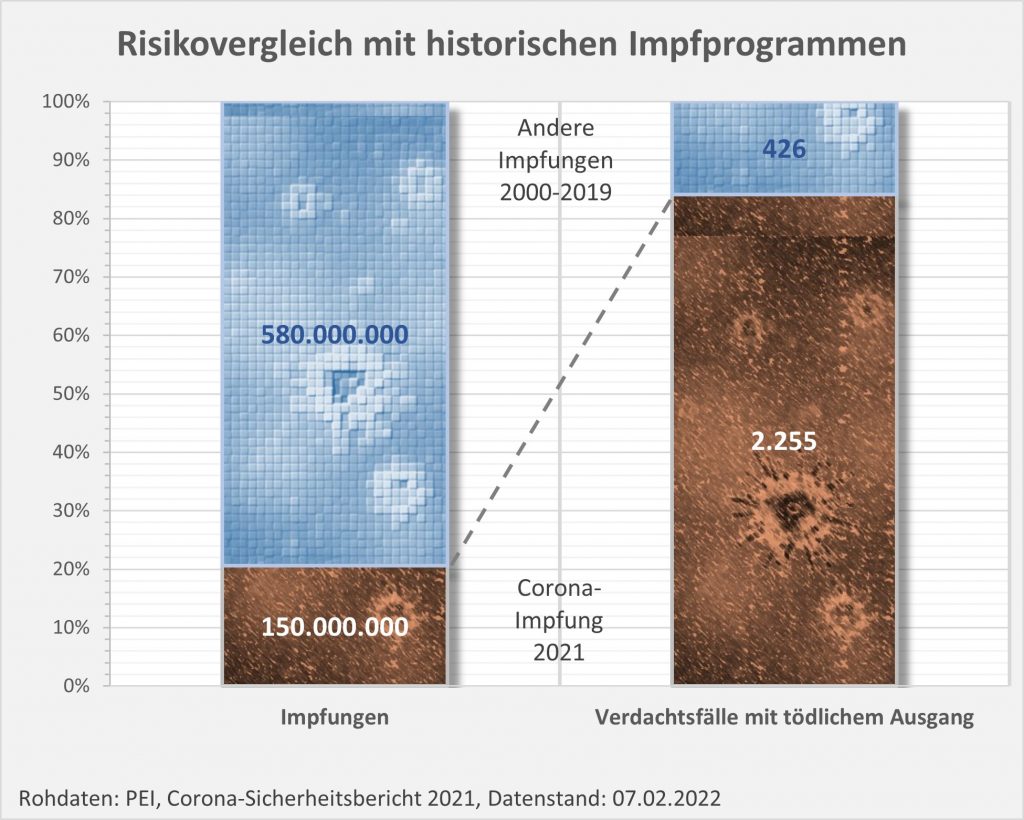
Abbildung 5: Risikovergleich mit historischen Impfprogrammen. Das relative Risiko bei der Corona-Impfung ist gegenüber den Vergleichsimpfungen um den Faktor 20 höher. Quelle: PEI, Corona-Sicherheitsbericht 2021, Datenstand: 07.02.2022.
Die Vergleichsdaten legen nahe, dass die aktuell verfügbaren Corona-Impfstoffe nicht zu den sichersten und harmlosesten Vakzinen gehören, die je entwickelt wurden. Selbstverständlich ändert das nichts daran, dass die Impfung in der weit überwiegenden Anzahl der Fälle nichtsdestotrotz Nutzen stiftet. Einige tausend Hochbetagte zusätzlich wären wohl ohne die Impfung Opfer des Virus geworden. Indessen sollte man angesichts der nüchternen Fakten Verständnis aufbringen für Menschen, die bezüglich der Corona-Impfung in ihrer eigenen Risikobewertung nach wie vor zögern. Vor allem auch eingedenk der nicht seriös ausschließbaren möglichen Langzeitfolgen, selbst wenn man die eher für unwahrscheinlich halten möge. Das Aufzeigen des Nutzens ist nur die eine Hälfte der nötigen Aufklärung, dazu gehört ebenso die offene Kommunikation bezüglich der möglichen Risiken.
An oder mit der Impfung verstorben?
Wir haben oben die statistisch zu erwartende Anzahl der Todesfälle in zeitlicher Nähe zur Impfung bestimmt. Dabei wurde das Verfahren des PEI angewendet (Bezug auf die mittlere Sterberate von 1,24% p.a.). Dieser Ansatz ist unscharf, insofern die Altersstruktur der Impfkohorte dabei keine Berücksichtigung findet. Das ist deswegen von Bedeutung, weil es natürlich einen Unterschied macht, ob ein 80-Jähriger innerhalb von 5 Tagen nach der Impfung verstirbt oder ob dasselbe einem 20-Jährigen widerfährt. Der Grund liegt auf der Hand: Letzterer hat ein etwa 160-mal geringeres allgemeines Sterberisiko. Wenn also der erste Fall eintritt, dann liegt das viel eher im Rahmen der Erwartung als im zweiten Fall. Diese Differenzierung geht in der pauschalen Betrachtung des PEI verloren.
Nun kennen wir nicht die genaue Zusammensetzung der an das PEI ergangenen Meldungen hinsichtlich der Altersstruktur. Wir haben aber hinreichende Kenntnis zu den altersabhängigen Impfquoten. Das erlaubt uns eine etwas schärfere Betrachtung im Hinblick auf die statistische Erwartung betreffend die Fallzahlen.
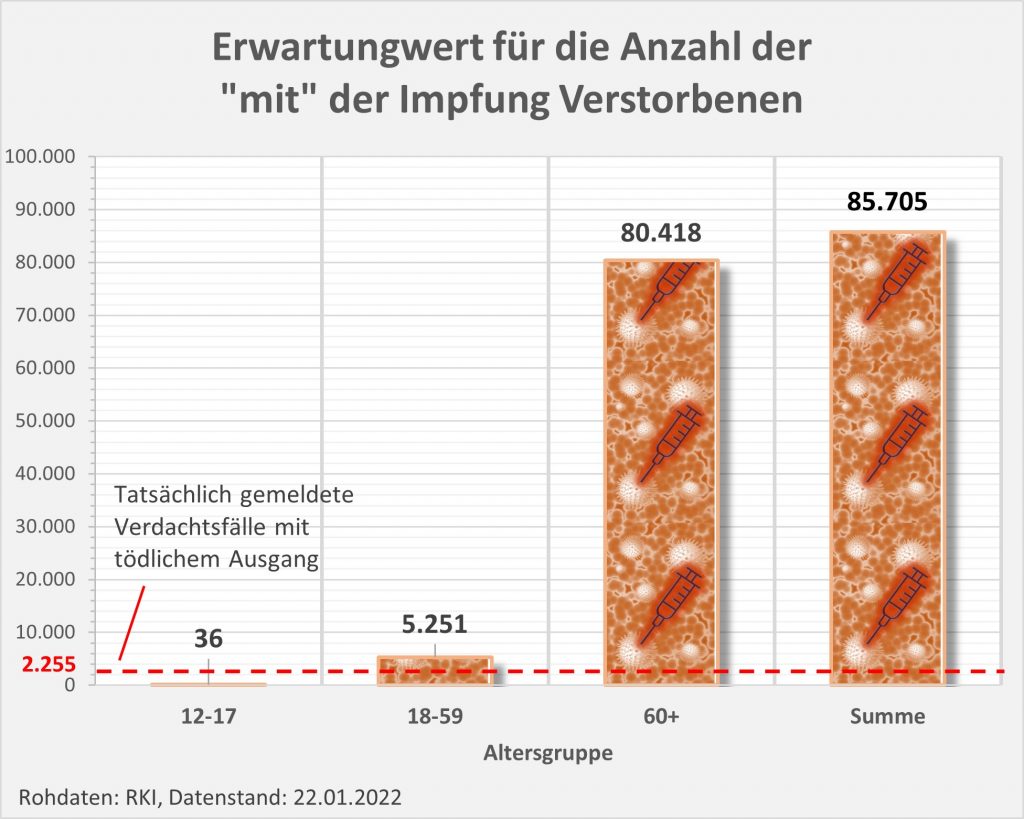
Abbildung 6: Statistische Erwartungswerte für die Anzahl der aufgrund des allgemeinen altersbezogenen Sterberisikos „an oder mit“ der Impfung innerhalb von 30 Tagen Verstorbenen. Die rot gestrichelte Linie markiert die an das PEI tatsächlich gemeldeten Fälle. Man sieht, dass tatsächlich nur ein winziger Bruchteil (1 von 38 Fällen) der innerhalb von 30 Tagen nach der Impfung statistisch zu erwartenden Todesfälle als Verdachtsfälle registriert wurden. Zugrunde gelegt wurden folgende Impfquoten (mit mindestens 1 Dosis): Altersgruppe 12-17: 55%, Altersgruppe 18-59: 80%, Altersgruppe 60+: 90%. Quelle für die Rohdaten: RKI, Datenstand: 07.02.2022.
Aus der vorstehenden Grafik wird klar ersichtlich, dass die Meldungen an das PEI nur einen winzigen Bruchteil der Todesfälle in zeitlicher Nähe zur Impfung (30 Tage) ausmachen. Die daraus im Hinblick auf mögliche Risikosignale resultierenden Fragen wurden oben angesprochen.
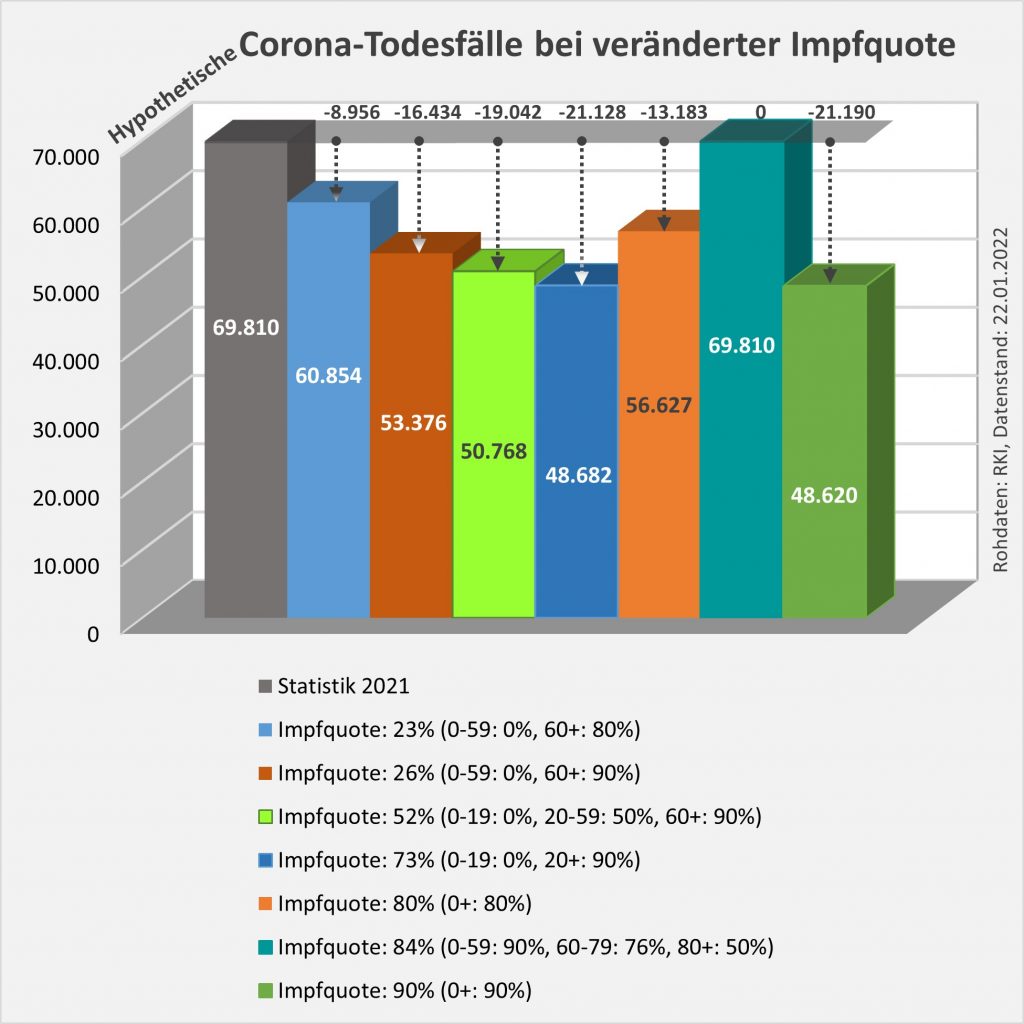
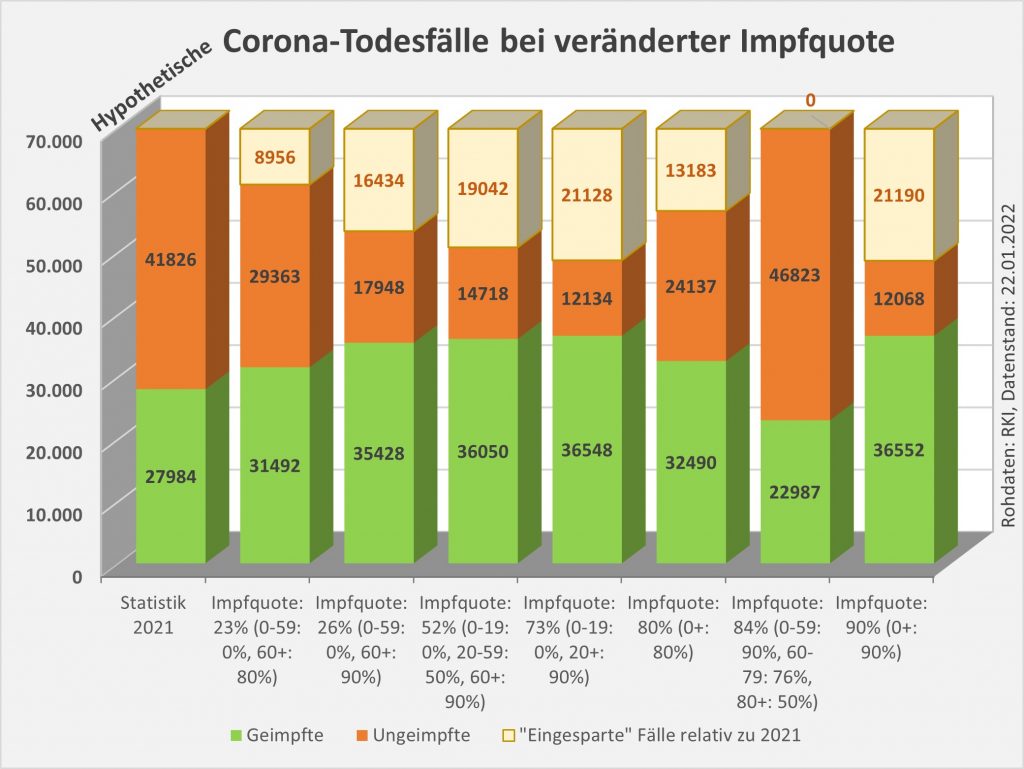
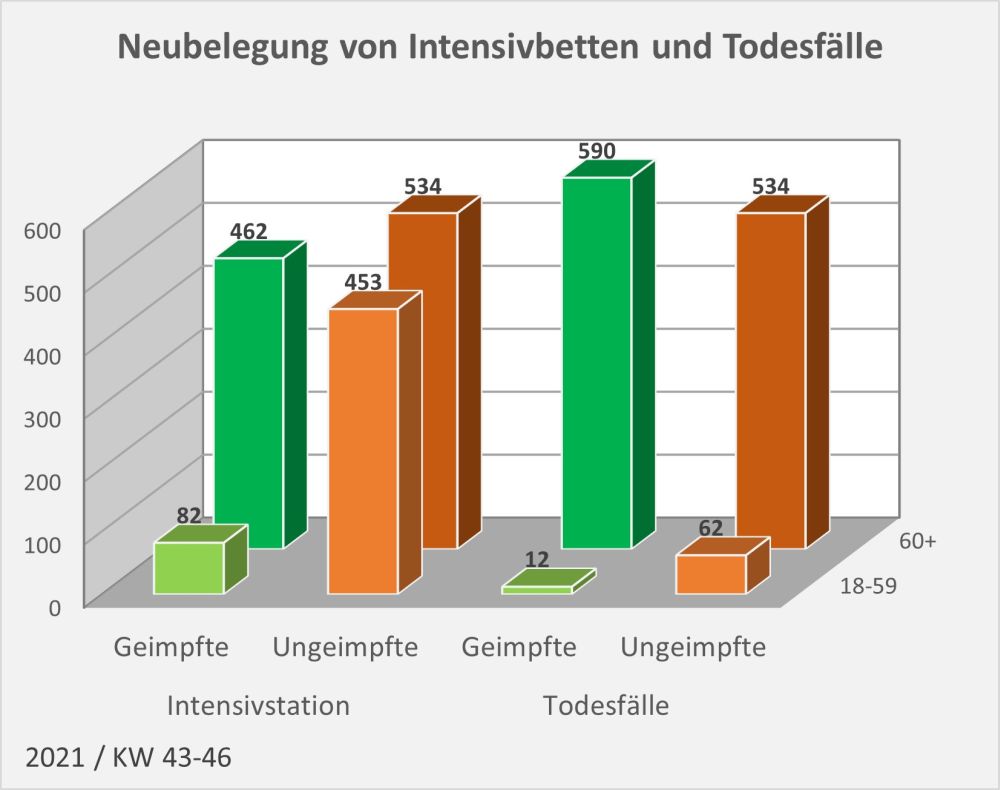
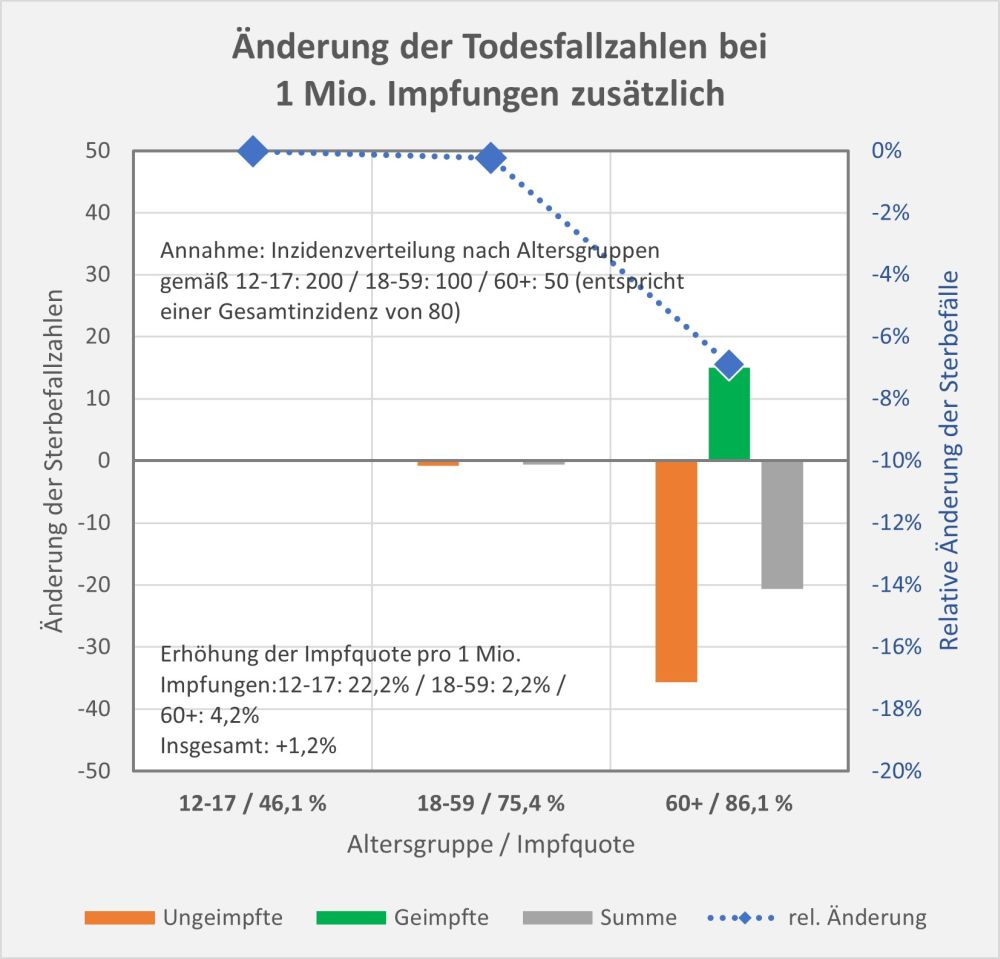
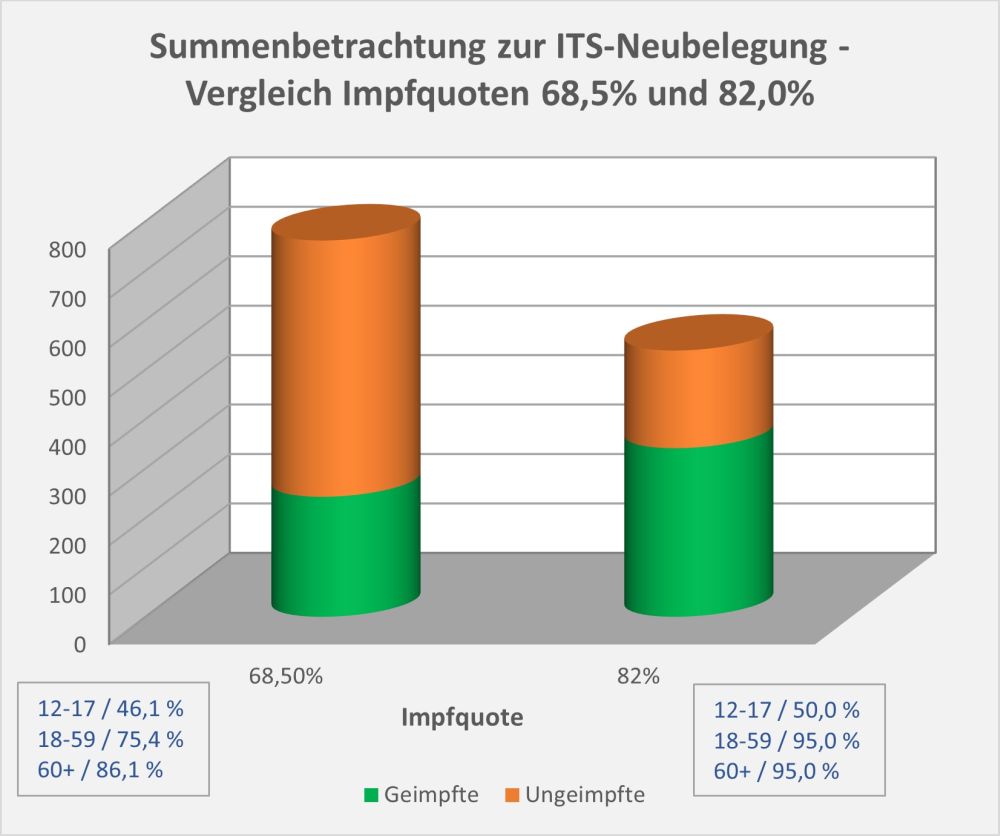
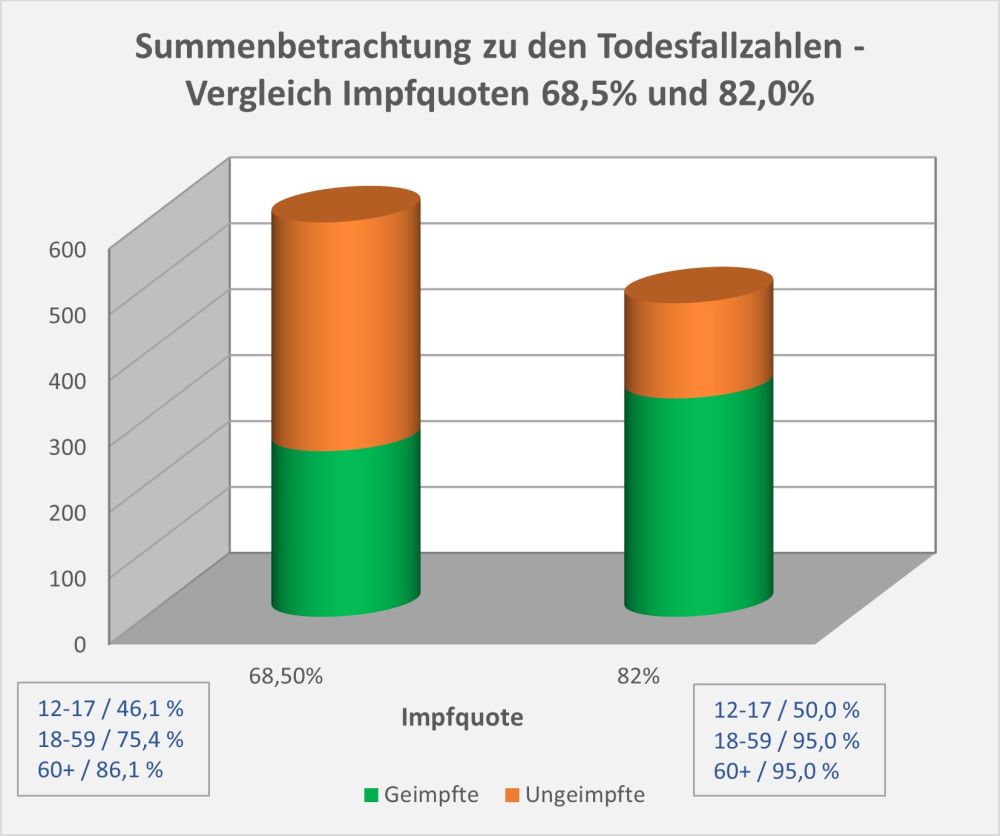
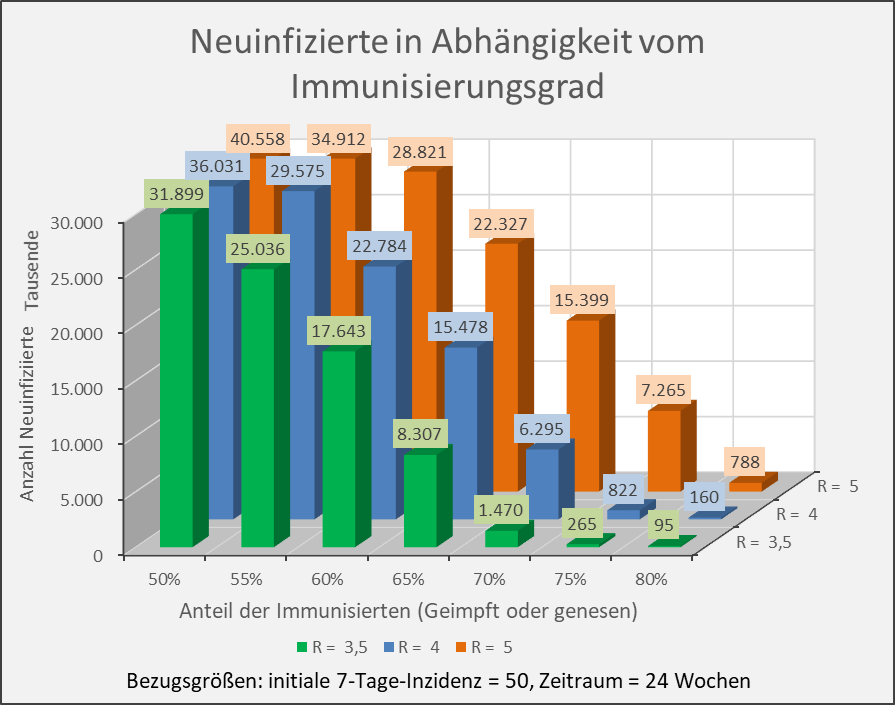
Man kann noch eine weitere, allerdings spekulative Analyse hinsichtlich der potentiell von der Impfung ausgehenden Sterbefälle anschließen. In [14] und [15] wurde gezeigt, wie die hypothetische Änderung der Wirksamkeit des Impfstoffs Einfluss nimmt auf die Anzahl der an oder mit Corona Verstorbenen.
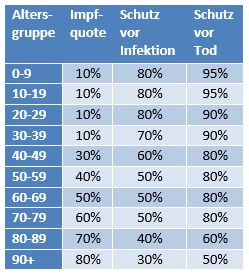
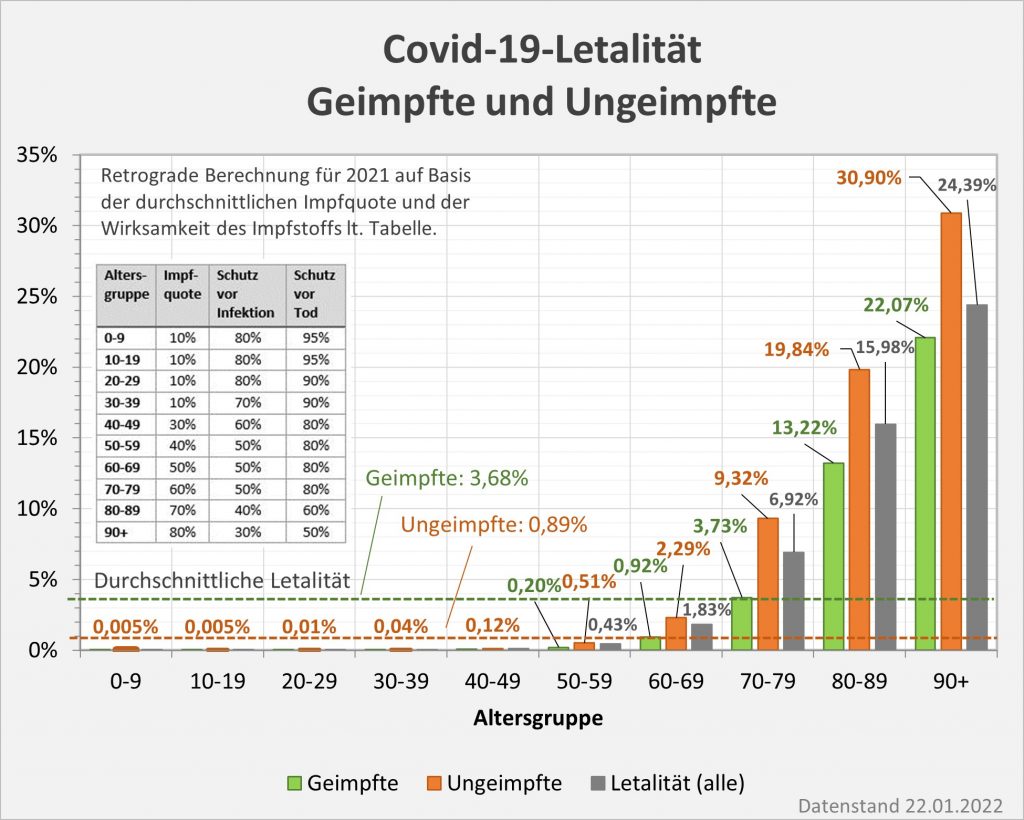
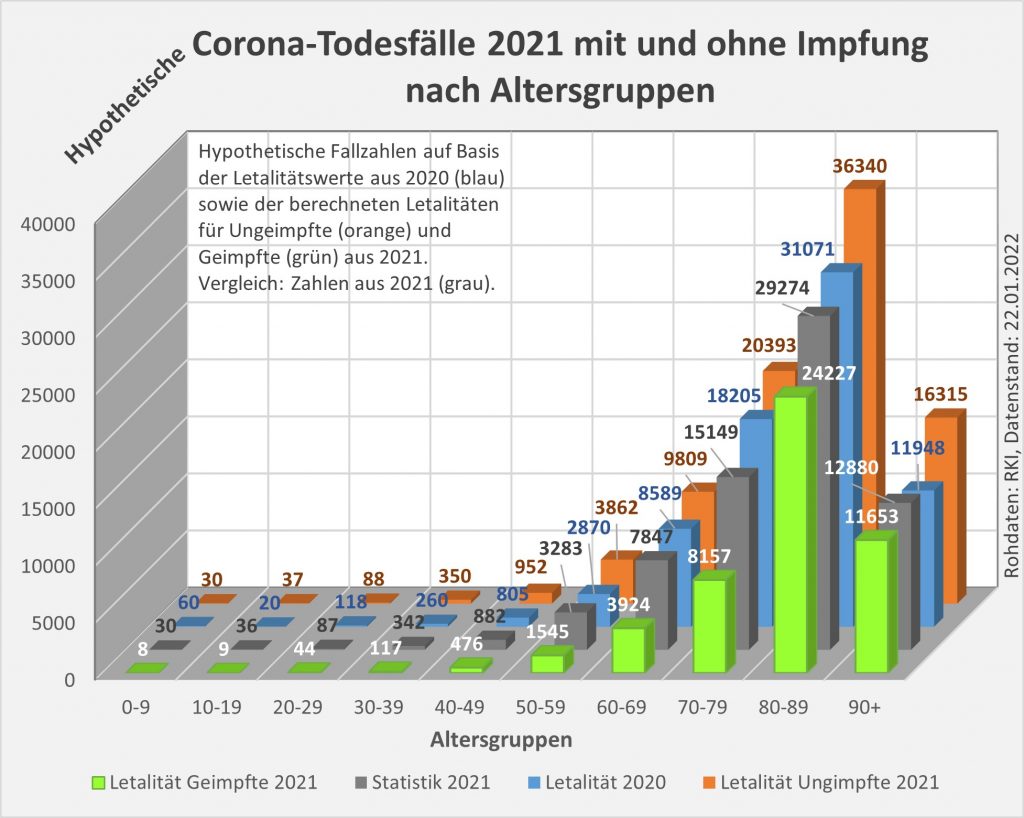
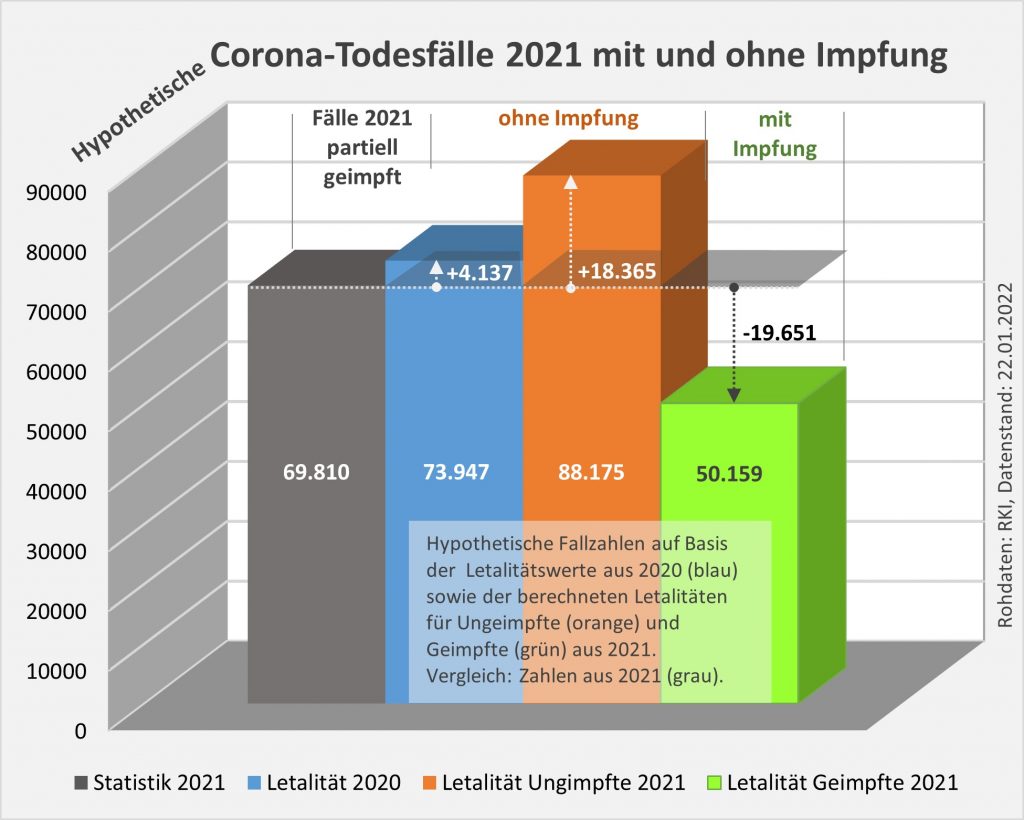
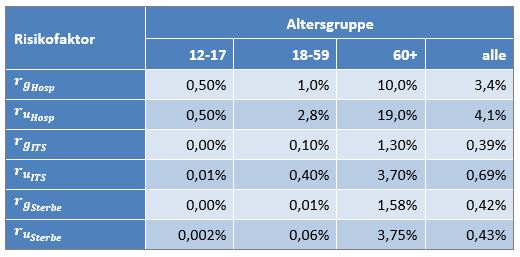
Damit können wir bestimmen, wie viele Geimpfte bei sonst gleichen Rahmenbedingungen bei einer geänderten Wirksamkeit des Impfstoffs an Corona verstorben wären. Aus der statistischen Analyse zu den Fallzahlen für 2020 und 2021 (s. [14]) ergibt sich, dass unter den knapp 70.000 an oder mit Corona Verstorbenen etwa 28.000 geimpft waren. Sie sind also trotz der Impfung Opfer des Virus geworden. Dabei wurden pro Altersgruppe unterschiedliche Impfquoten und Wirksamkeiten des Impfstoffs unterstellt (s. Tab. 1, Spalten 2, 3 und 5).
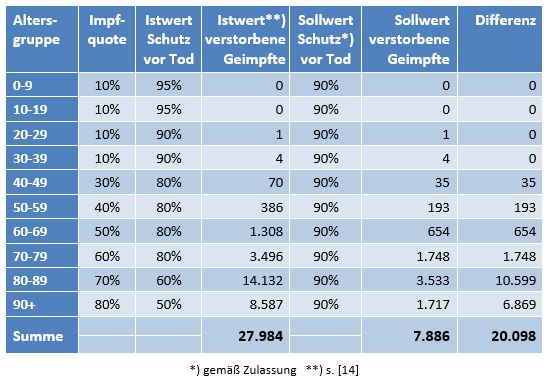
Tabelle 1: Annahmen zu den altersgruppenspezifischen Impfquoten und den Schutzwirkungen der Impfung vor Tod (an oder mit Corona). Die durchschnittlichen Impfquoten ergeben sich aus dem Verlauf der Impfkampagne im Jahresverlauf aus den Daten des RKI. Die Annahmen zur Schutzwirkung basieren auf den Infektionszahlen und den Todesfallzahlen Geimpfter und Ungeimpfter. Die Istwerte zu den Verstorbenen Geimpften wurden auf Basis des in [14] beschriebenen Modells berechnet. Die Sollwerte ergeben sich aus der im Text dargelegten Überlegung. Generell muss man anmerken, dass vielfach keine genauen Zahlen zu Geimpften und Ungeimpften publiziert werden, deshalb wurden die Werte methodisch abgeschätzt (s. [14]).
Laut Zulassungsstudien sollte die Schutzwirkung vor Tod für alle Altersgruppen bei mindestens 90 % gelegen haben. Das trifft jedenfalls auf die beiden meistgeimpften Vakzine von Biontech und Moderna zu. Indes ist diese hohe Schutzwirkung nicht vereinbar mit der beobachteten großen Anzahl der an oder mit Corona verstorbenen Geimpften. Um den Unterschied zu den realen Fallzahlen aufzulösen, gibt es zwei Ansätze: 1. Die tatsächliche Wirksamkeit (in Tab. 1 „der Istwert“) war deutlich geringer. Das wurde in [14] behandelt. 2. Die Wirksamkeit war unverändert hoch (in Tab. 1 „der Sollwert“), wie vom Hersteller angegeben, aber die Betroffenen sind zu einem gewissen Anteil nicht an oder mit Corona verstorben, sondern an oder mit der Corona-Impfung.
Es gilt als Sakrileg, überhaupt nur die Möglichkeit zu erörtern, von der Corona-Impfung könne eine Gefährdung ausgehen. Indes geht es hier nicht um Glauben, sondern darum, Antworten auf offene Fragen zu finden. Daher ist es zulässig, die aus dem Grundgedanken von Punkt 2 resultierenden Konsequenzen näher zu beleuchten. Das ändert freilich nichts daran, dass die Überlegungen dazu zum jetzigen Zeitpunkt ganz klar spekulativen Charakter haben. Inwieweit die Impfung Risiken birgt, eventuell auch ernsthafte, ist letztlich eine medizinische Frage. Angesichts der nur höchst unzureichend erfassten und ungenauen Daten hinsichtlich fast aller Aspekte der Pandemie – ein Armutszeugnis für einen Industrie- und Wissenschaftsstandort – muss die Aussagekraft der Statistik zwangsläufig beschränkt bleiben.
Im Falle von Punkt 2 können wir die hypothetische Anzahl der an oder mit Corona verstorbenen Geimpften unter der Annahme der Soll-Wirksamkeit direkt aus der beobachteten Fallzahl bei der Ist-Wirksamkeit berechnen.
Sei die beobachtete Ist-Wirksamkeit des Impfstoffs und
die hypothetische Soll-Wirksamkeit. Entsprechend bezeichnen wir mit
die tatsächliche Anzahl der verstorbenen Geimpften und mit
die hypothetische Anzahl unter der Annahme der Soll-Wirksamkeit. Es gilt folgender Zusammenhang (s. [14], Analogie zu Formel (34) bei unveränderter Impfquote):
(1)
Die damit unter der Annahme eines über alle Altersgruppen wirksamen Schutzes vor Tod in Höhe von 90 % (=Soll-Wirksamkeit) errechneten Zahlenwerte finden sich in Tab. 1. Insgesamt ergeben sich statt der 28.000 Todesfälle an oder mit Corona (unter Geimpften) nur knapp 8.000 Fälle (s. Tab. 1, Spalte 6, „Sollwert verstorbene Geimpfte“), die im engeren Sinne an oder mit Corona verstorben sein könnten. Wobei angemerkt werden soll, dass die solchermaßen errechneten Zahlen unsicher sind. Die tatsächliche Wirksamkeit der Impfstoffe ist eben nicht mit der nötigen Genauigkeit bekannt. Bei einer Unschärfe von 10 % könnte der Sollwert in Spalte 6 auch bei etwa 16.000 Fällen zu liegen kommen, so dass am Ende nicht 20.000, sondern nur 12.000 Sterbefälle verblieben (Spalte ganz rechts).
Die Differenz von 20.000 (oder evtl. auch nur 12.000) ginge somit potentiell auf das Konto der Impfung, so dass wir diesbezüglich sagen könnten, „an oder mit Corona oder an oder mit der Corona-Impfung“ verstorben. Diese Interpretation steht nicht im Widerspruch zur Anzahl der an das PEI gemeldeten Verdachtsfälle mit tödlichem Ausgang, da der statistische Erwartungswert dafür sogar innerhalb der ersten 30 Tage nach der Impfung bei über 80.000 Personen liegt, übers volle Jahr gerechnet sogar bei ca. 1 Mio. Toten. Die genannte Zahl von potentiell 20.000 Toten macht daher an den innerhalb von 12 Monaten nach der Impfung Verstorbenen einen Anteil von nur 2,2 % aus. Es gibt also kein statistisches Missverhältnis.
Damit wird nicht behauptet, die genannten 20.000 (oder evtl. auch nur 12.000) Sterbefälle seien definitiv auf die Impfung zurückzuführen. Mit dieser Interpretation würde man die Beweiskraft der Statistik weit überschätzen. Evidenz kann man an dieser Stelle nur auf der Basis von gezielten Untersuchungen der Einzelfälle, im Extremfall also aller verstorbenen positiv getesteten Geimpften, erlangen. Im Minimum sind statistisch signifikante Stichproben erforderlich. Unabhängig davon könnte eine kausal auf die Impfung zurückzuführende und in der beschriebenen Weise erhöhte Sterblichkeit von etwa 0,033 % (= 20.000/61,5 Mio.) die trotz der Verfügbarkeit von im Prinzip hochwirksamen Impfstoffen beobachtete leichte Übersterblichkeit schlüssig erklären. Nichtsdestotrotz bleibt diese Folgerung eine Spekulation, da sie mit rein statistischen Mitteln nicht verifiziert werden kann.
An oder mit Corona verstorben?
Die Todesfallzahlen betreffend Corona sind bekanntermaßen immer mit dem Zusatz „an oder mit“ Corona verstorben versehen. In der öffentlichen Wahrnehmung geht das zunehmend unter. Man kann davon ausgehen, dass die knapp 70.000 Coronatoten in 2021 von einer großen Mehrheit als kausal auf Corona zurückzuführende Fälle verstanden werden. Und in diesem Sinne werden die Zahlen auch kommuniziert. In wie vielen Fällen Corona tatsächlich die Todesursache ist, das ist völlig offen.
Man muss den Eindruck gewinnen, dass es auch niemand interessiert. Es gibt allenfalls einige wenige kritische Stimmen. Genaueres weiß man schlechterdings nicht. Mal liest man die Schlagzeile „29 % der Coronatoten gar nicht an Corona verstorben“, mal hört man gar von bis zu 80 % Fällen, bei denen Corona zumindest nur einer von mehreren Faktoren gewesen sein soll. Letzten Endes sind diese Angaben sämtlich nicht vertrauenswürdig, weil ihnen die wissenschaftliche Grundlage fehlt. Dafür müsste man die Todeskausalität in jedem Einzelfall untersuchen, oder zumindest statistisch signifikante Stichproben nehmen. Warum Letzteres nicht systematisch umgesetzt wird, ist nur eine von vielen unwissenschaftlichen Auffälligkeiten im Pandemiemanagement.
An dieser Stelle kann man dennoch die Plausibilität der Corona-Todesfallzahlen mittels statistischer Methoden auf die Probe stellen. Dazu nehmen wir die Zahl der „an oder mit“ Corona Verstorbenen und vergleichen sie mit der statistisch zu erwartenden Anzahl der Todesfälle im Vergleichszeitraum. Wir fragen also konkret, wie viele der positiv auf Corona getesteten Personen wären denn aufgrund der altersabhängigen statistischen Sterbewahrscheinlichkeit im Vergleichszeitraum gestorben. Im Grundsatz handelt es sich hierbei und dasselbe Verfahren, wie es auch vom Paul-Ehrlich-Institut betreffend die Impfungen im Hinblick auf die Verdachtsfälle mit tödlichem Ausgang angewandt wird.
Die Resultate sind in den Säulendiagrammen Abb. 7, 8 und 9 dargestellt.
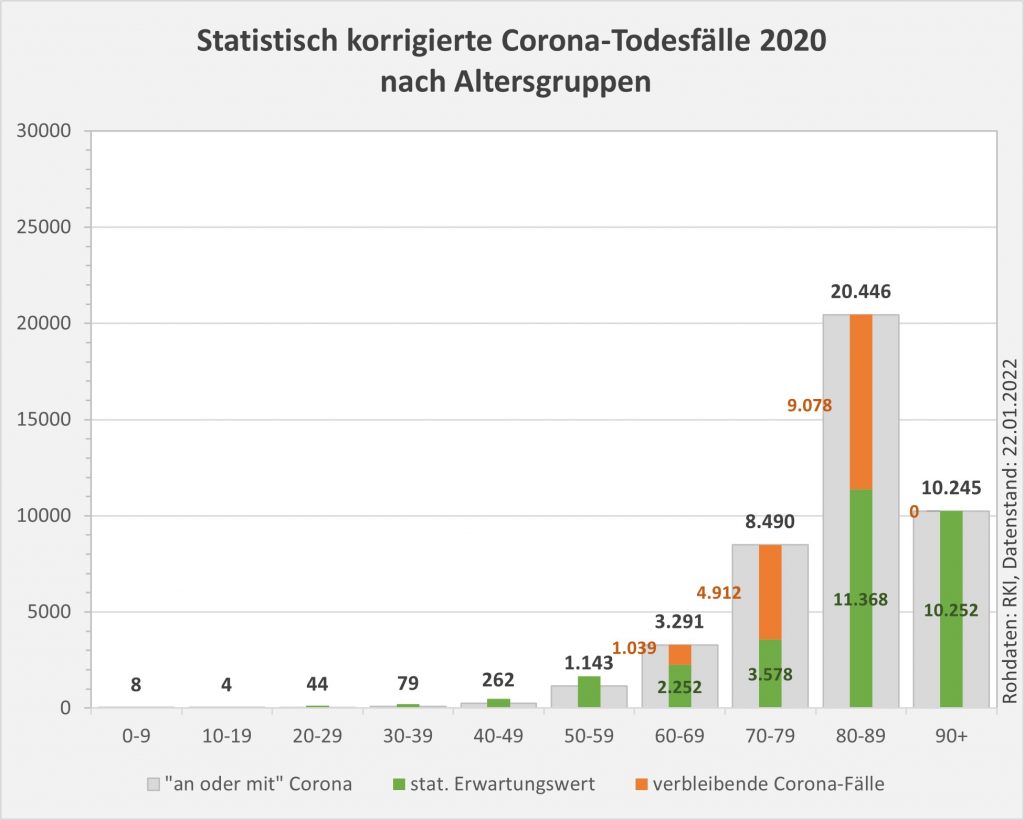
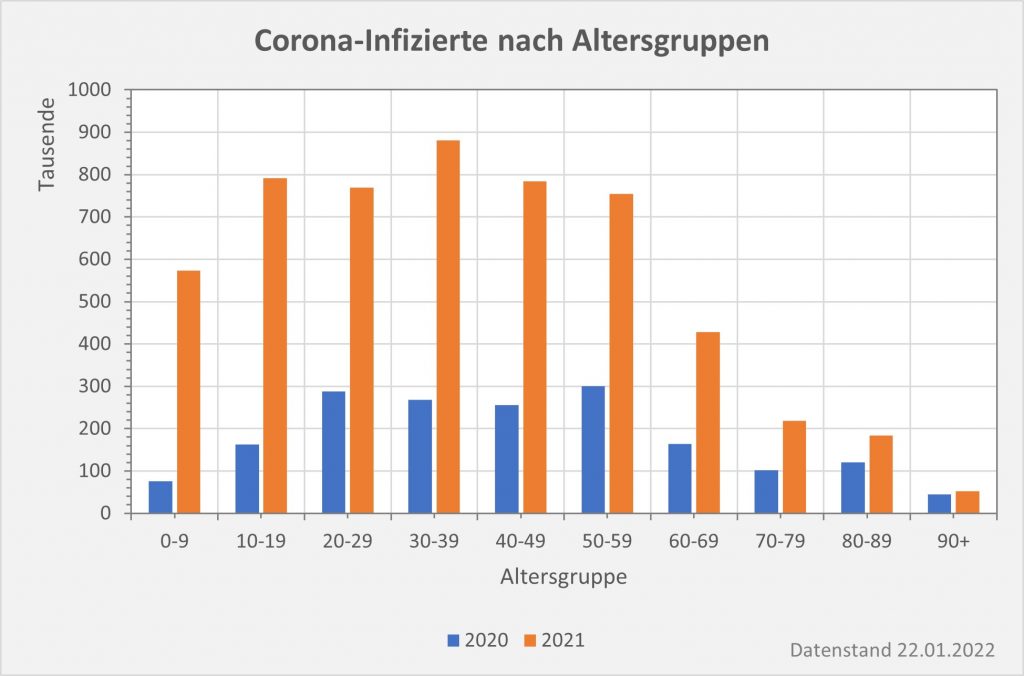
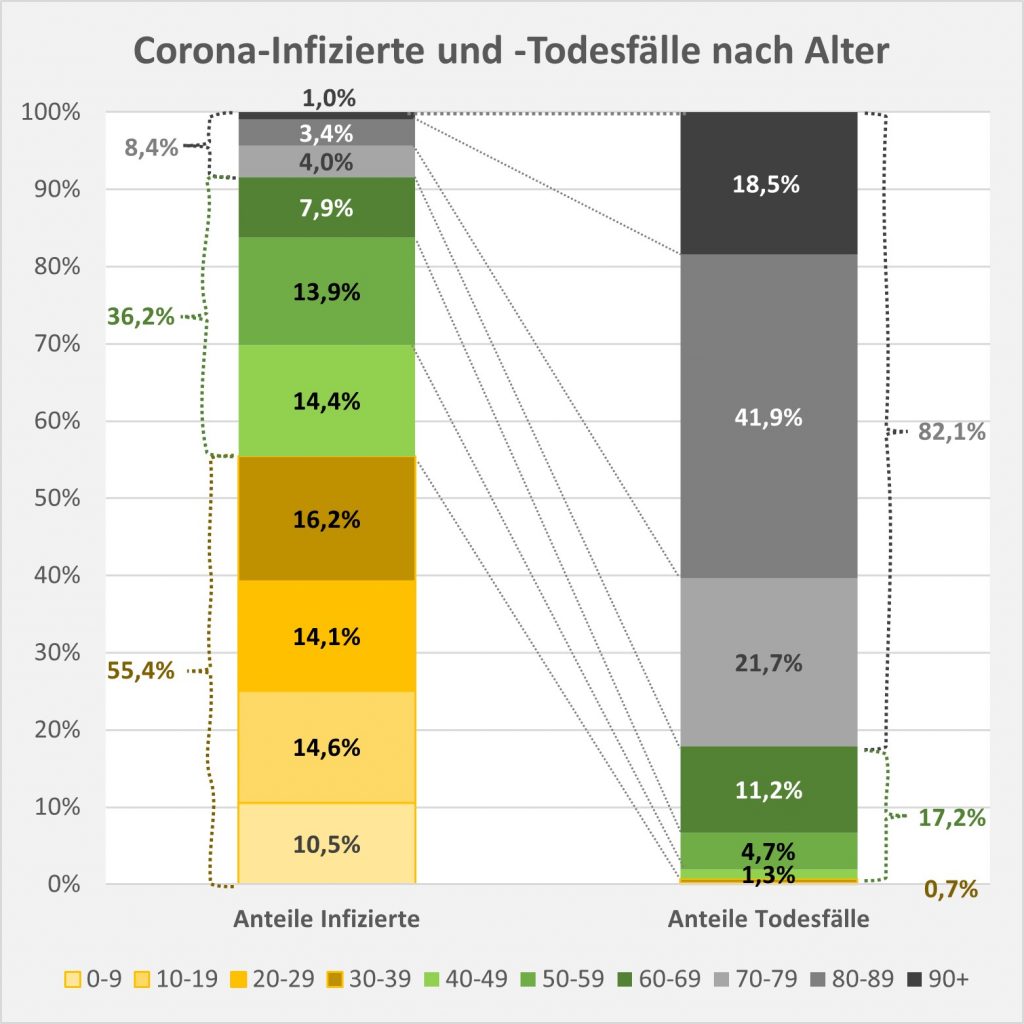
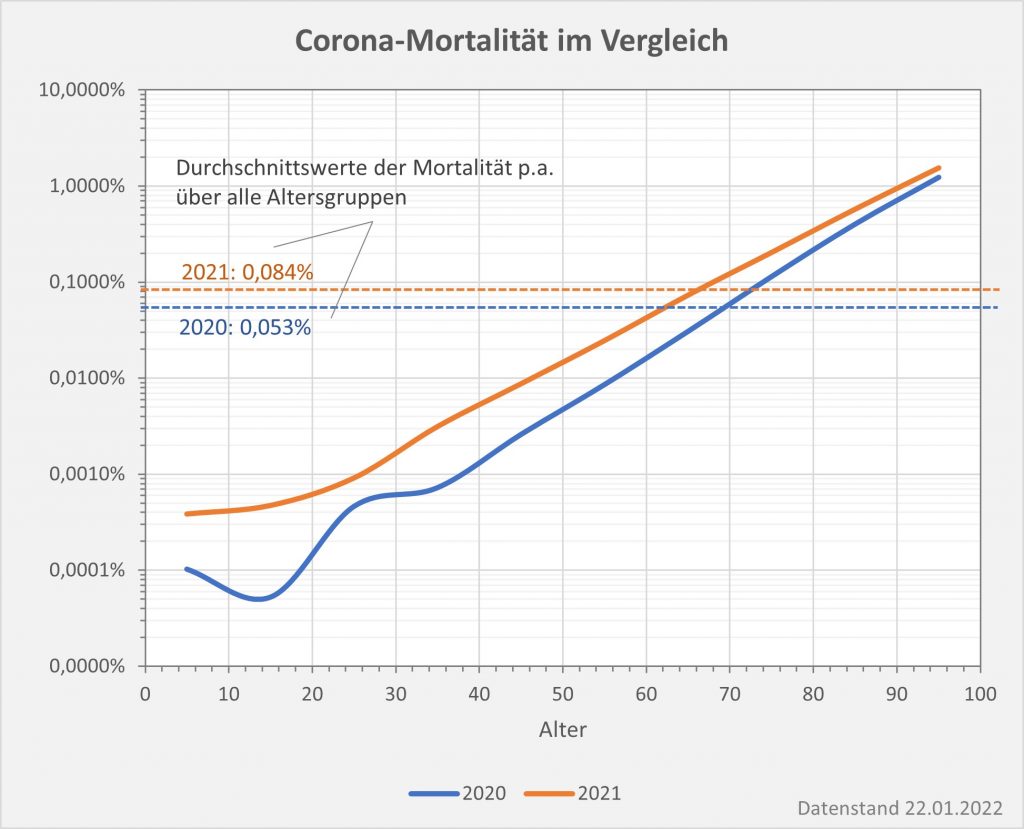
Abbildung 7: Vergleich der Sterbefälle „an oder mit“ Corona mit den in 2020 unter den Infizierten aufgrund des allgemeinen altersbezogenen Sterberisikos statistisch zu erwarten gewesenen Todesfällen. Graue Säulen: „an oder mit“ Corona verstorben, wie vom RKI dokumentiert. Grün: statistischer Erwartungswert der Todesfälle p.a. unter den positiv Getesteten. Orange: verbleibende Todesfälle nach Abzug des Erwartungswerts, die man im statistischen Abgleich als Corona-bedingte Sterbefälle werten kann. Nur die Letzteren sind zusätzliche Todesfälle. In den Altersgruppen unter 60 liegt der statistische Erwartungswert über der Anzahl der registrierten Corona-Sterbefälle. Bei den Über-60-Jährigen verbleiben nach Abzug der erwarteten Todesfälle je nach Altersgruppe 1000 bis 9.000 Fälle, die man im Hinblick auf das allgemeine Sterberisiko statistisch Corona zurechnen kann. Rohdaten: RKI, Datenstand: 22.01.2022.
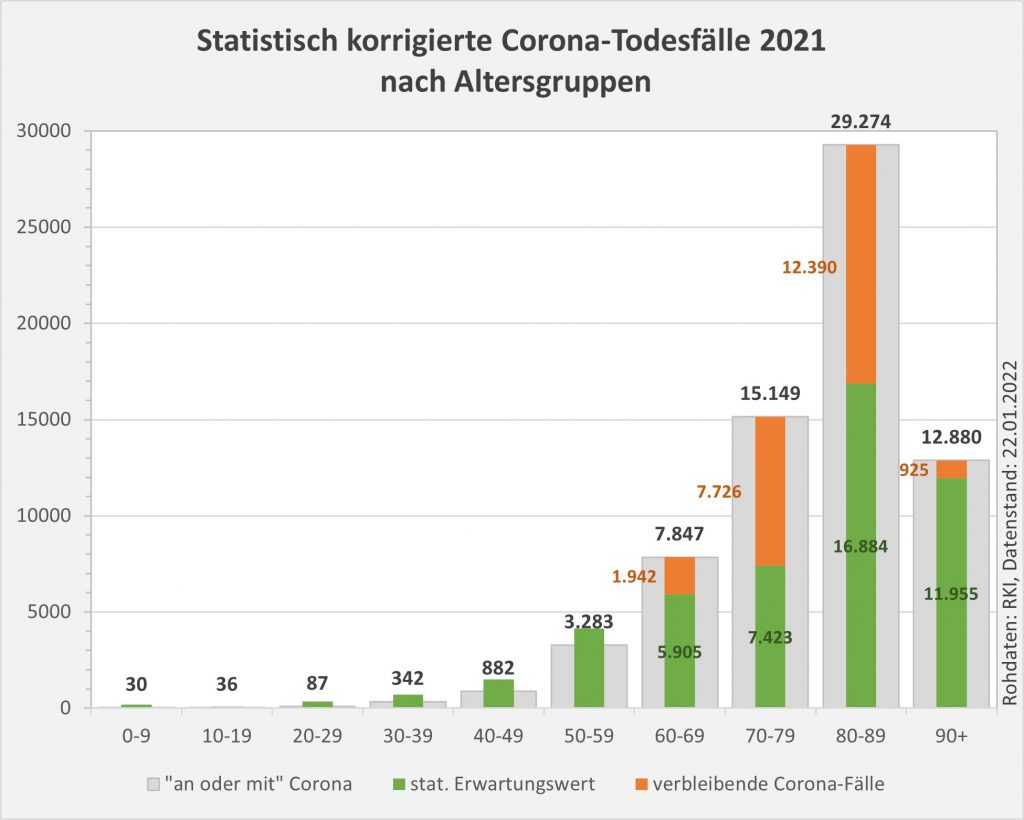
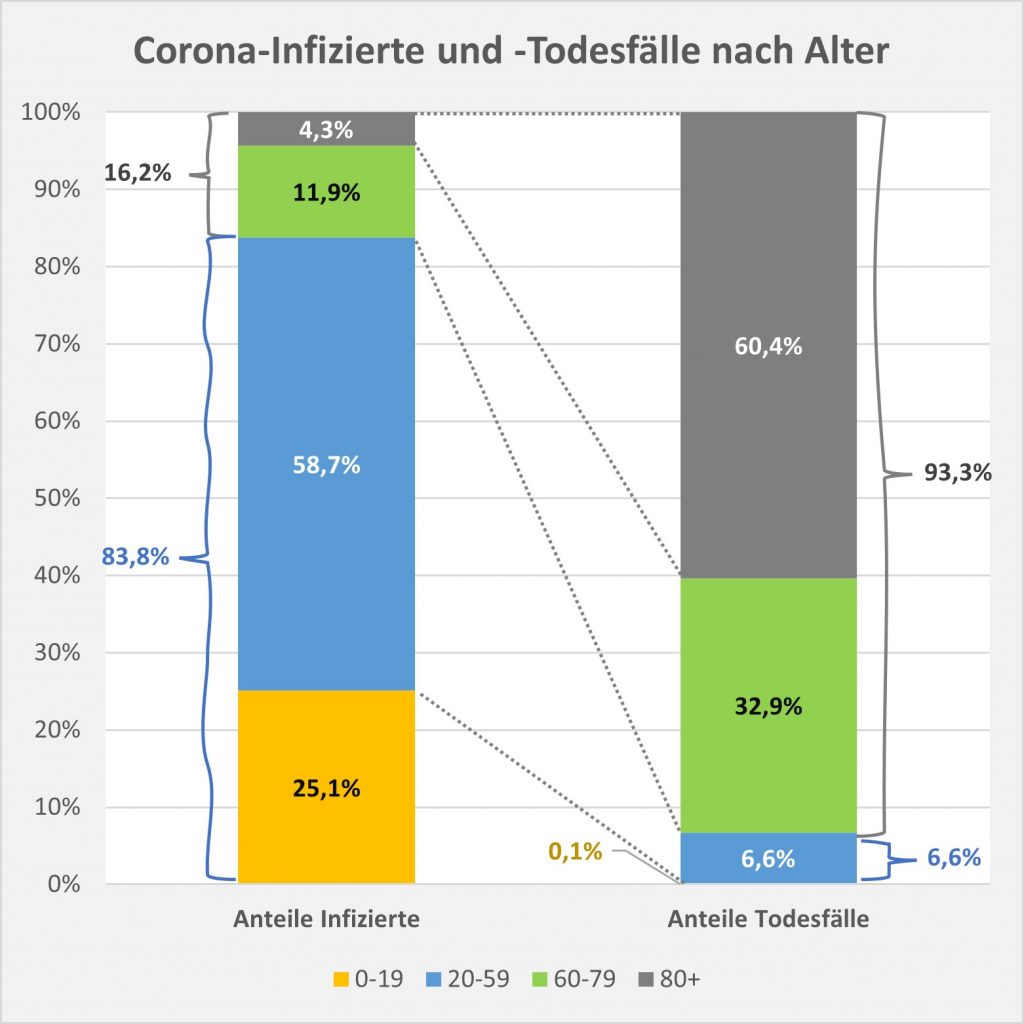
Abbildung 8: Vergleich der Sterbefälle „an oder mit“ Corona mit den in 2021 unter den Infizierten aufgrund des allgemeinen altersbezogenen Sterberisikos statistisch zu erwarten gewesenen Todesfällen. Graue Säulen: „an oder mit“ Corona verstorben, wie vom RKI dokumentiert. Grün: statistischer Erwartungswert der Todesfälle p.a. unter den positiv Getesteten. Orange: verbleibende Todesfälle nach Abzug des Erwartungswerts, die man im statistischen Abgleich als Corona-bedingte Sterbefälle werten kann. Nur die Letzteren sind zusätzliche Todesfälle. In den Altersgruppen unter 60 liegt der statistische Erwartungswert über der Anzahl der registrierten Corona-Sterbefälle. Bei den Über-60-Jährigen verbleiben nach Abzug der erwarteten Todesfälle je nach Altersgruppe knapp 1000 bis zu 12.000 Fälle, die man im Hinblick auf das allgemeine Sterberisiko statistisch Corona zurechnen kann. Rohdaten: RKI, Datenstand: 22.01.2022.
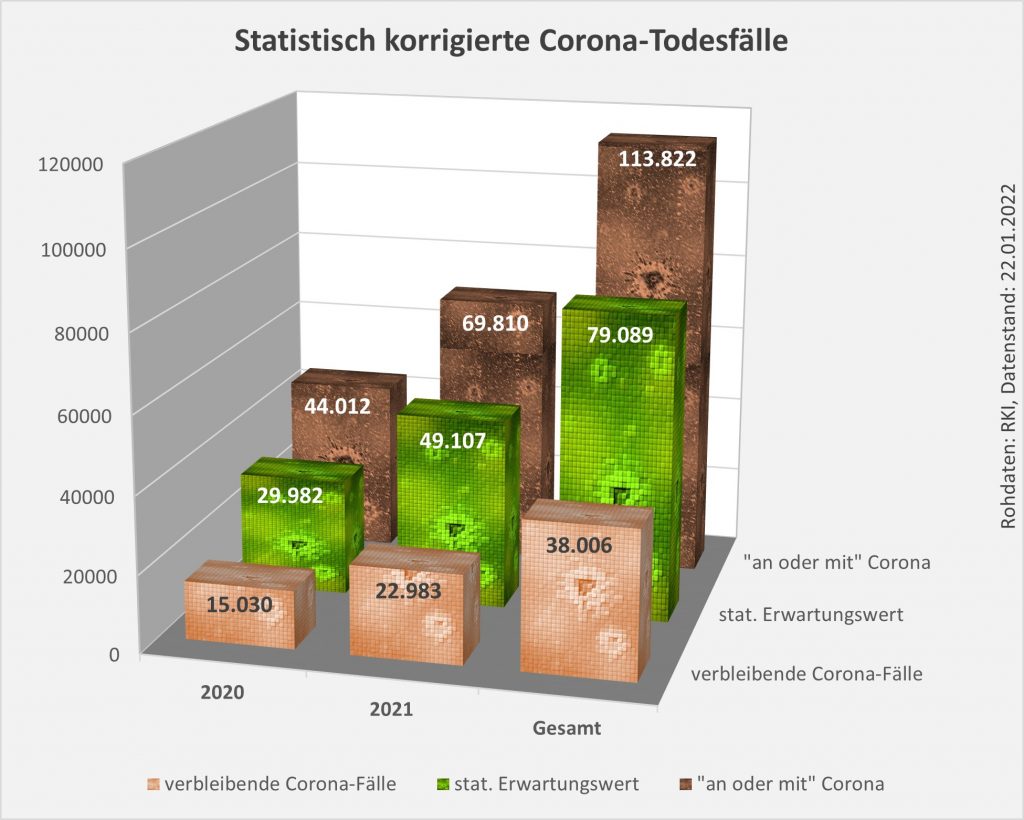
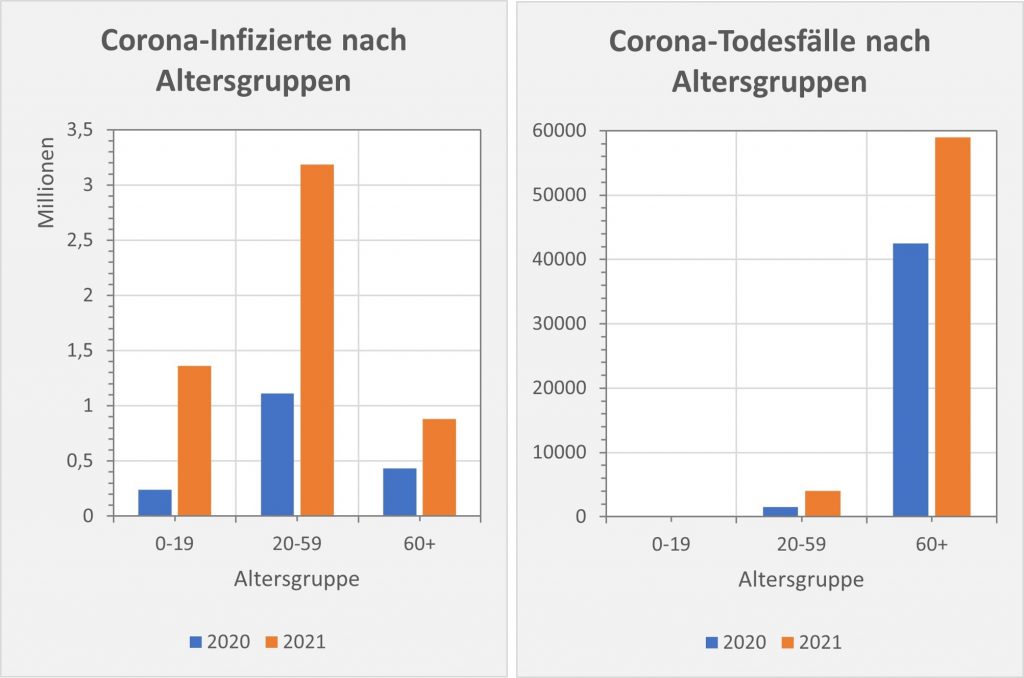
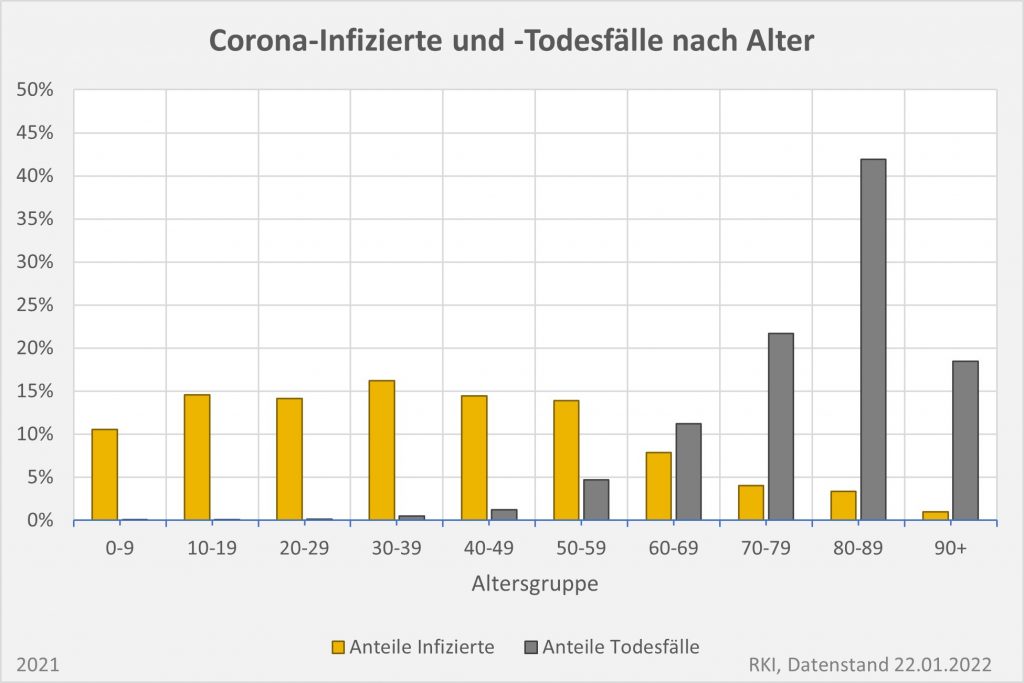
Abbildung 9: Vergleich der Sterbefälle „an oder mit“ Corona in 2020, 2021 und insgesamt mit den unter den Infizierten aufgrund des allgemeinen altersbezogenen Sterberisikos statistisch zu erwarten gewesenen Todesfällen. In beiden Jahren liegt der statistische Erwartungswert der Todesfälle unter der Anzahl der registrierten Corona-Sterbefälle. Nach Abzug der erwarteten Todesfälle verbleiben in 2020 etwa 15.000 und in 2021 etwa 23.000 Fälle, die man im Hinblick auf das allgemeine Sterberisiko statistisch Corona zurechnen kann. Für beide Jahre zusammen sind das in Summe 38.000 Todesfälle. Rohdaten: RKI, Datenstand: 22.01.2022.
Vermöge der vorstehenden Diagramme wird selbstredend nicht belegt oder gar bewiesen, die Anzahl der Coronatoten belaufe sich über beide Jahre tatsächlich nur auf 38.000 statt knapp 114.000. Die Todeskausalität ist – bis auf die wenigen Fälle, in denen sie mittels einer pathologischen Untersuchung zweifelsfrei bestimmt wurde – im Allgemeinen als offen anzusehen. Deswegen muss man auch korrekterweise immer den Zusatz „an oder mit“ davorsetzen. Aus der statistischen Analyse ergibt sich allerdings schon, dass die Zweifel an der hohen Gesamtanzahl der Corona zugerechneten Sterbefälle durchaus berechtigt sind. Zumindest kann man folgendes festhalten:
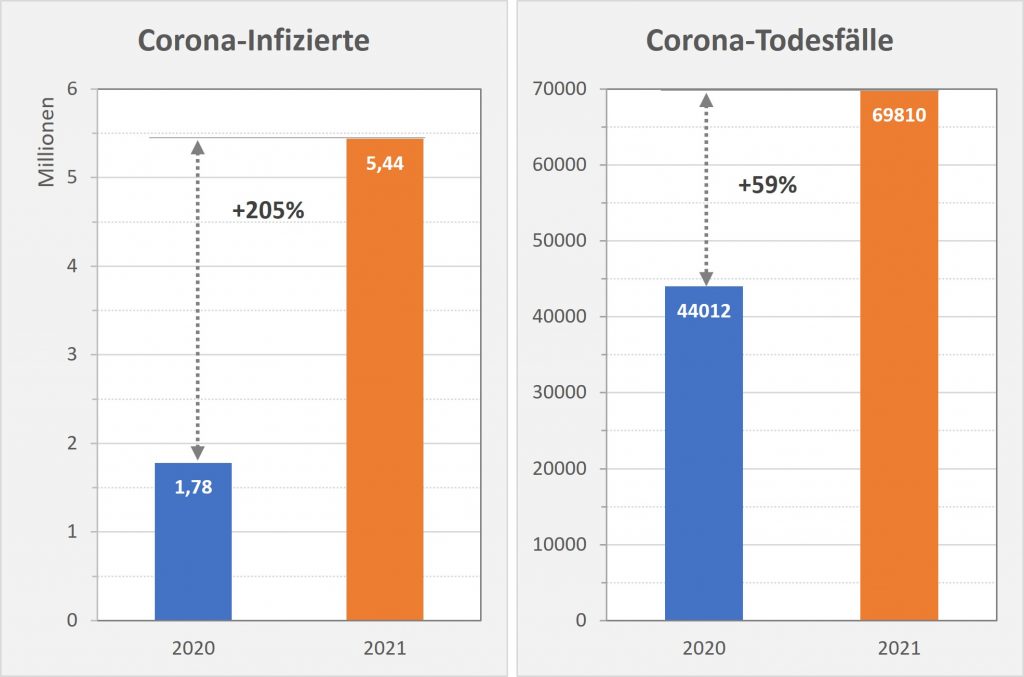
- In 2020 wären etwa 30.000 der insgesamt 44.012 „an oder mit“ Corona im Laufe des Jahres Verstorbenen aufgrund der altersbedingten allgemeinen Sterblichkeit der Infizierten im statistischen Mittel auch ohne die Corona-Infektion verstorben (genauer, innerhalb von 12 Monaten nach dem Positivtest). Nur etwa 32 % der offiziell als Coronatote gezählten Sterbefälle (15.000) sind damit aus statistischer Sicht als zusätzliche Todesfälle zu werten. Das deckt sich im Übrigen mit der rechnerisch bestimmten Übersterblichkeit für 2021, die im Bereich von etwa 1,5 % – 2 % aller Sterbefälle, also bei knapp 20.000 liegt.
- In 2021 wären etwa 49.000 der insgesamt 69.810 „an oder mit“ Corona im Laufe des Jahres Verstorbenen aufgrund der altersbedingten allgemeinen Sterblichkeit der Infizierten im statistischen Mittel auch ohne die Corona-Infektion verstorben (genauer, innerhalb von 12 Monaten nach dem Positivtest). Nur etwa 30 % der offiziell als Coronatote gezählten Sterbefälle (23.000) sind damit aus statistischer Sicht als zusätzliche Todesfälle zu werten. Das deckt sich auch hier mit der rechnerisch bestimmten Übersterblichkeit für 2021, die im Bereich von etwa 2 % aller Sterbefälle, also bei etwa 20.000 Toten liegt.
- In der Gesamtschau zur Pandemie wären damit etwa 79.000 der insgesamt knapp 114.000 „an oder mit“ Corona Verstorbenen aufgrund der altersbedingten allgemeinen Sterblichkeit der positiv Getesteten im statistischen Mittel auch ohne die Corona-Infektion innerhalb einer Zeitspanne von 12 Monaten nach dem Positivtest verstorben. Nur etwa 31 % der offiziell als Coronatote gezählten Sterbefälle (38.000) sind somit aus statistischer Sicht als zusätzliche Todesfälle zu werten. Diese Zahl spiegelt die durch Corona verursachte rechnerische Übersterblichkeit in Höhe von etwa 2 % wider.
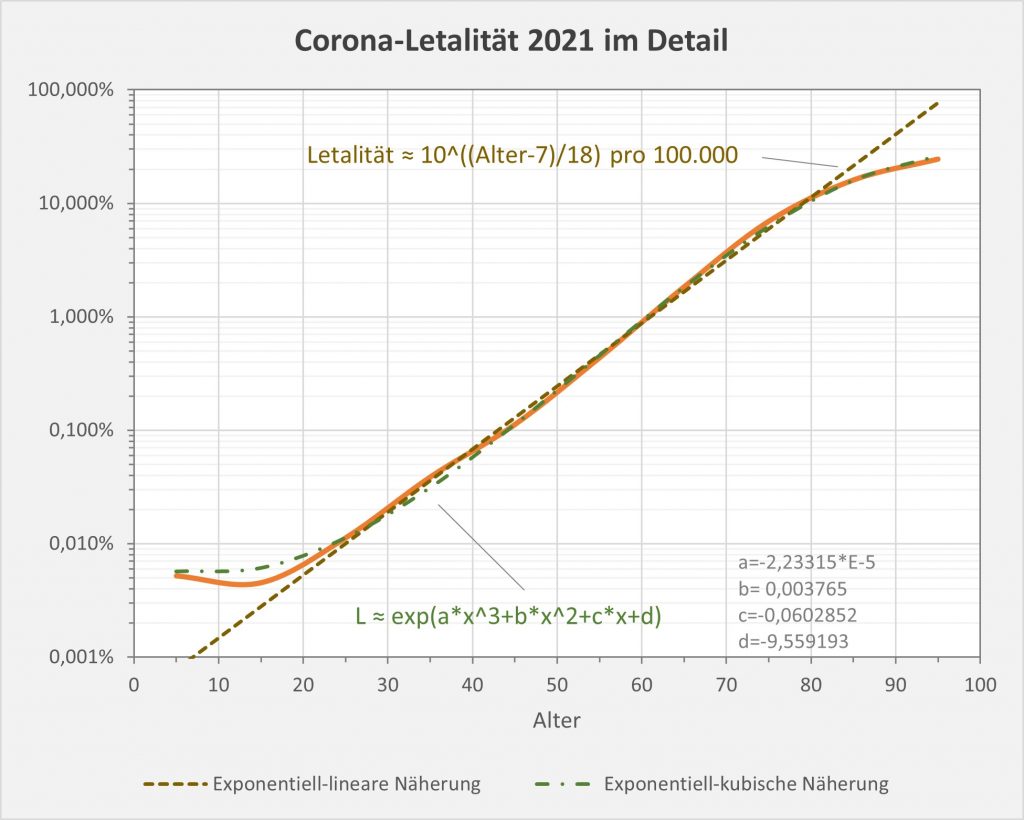
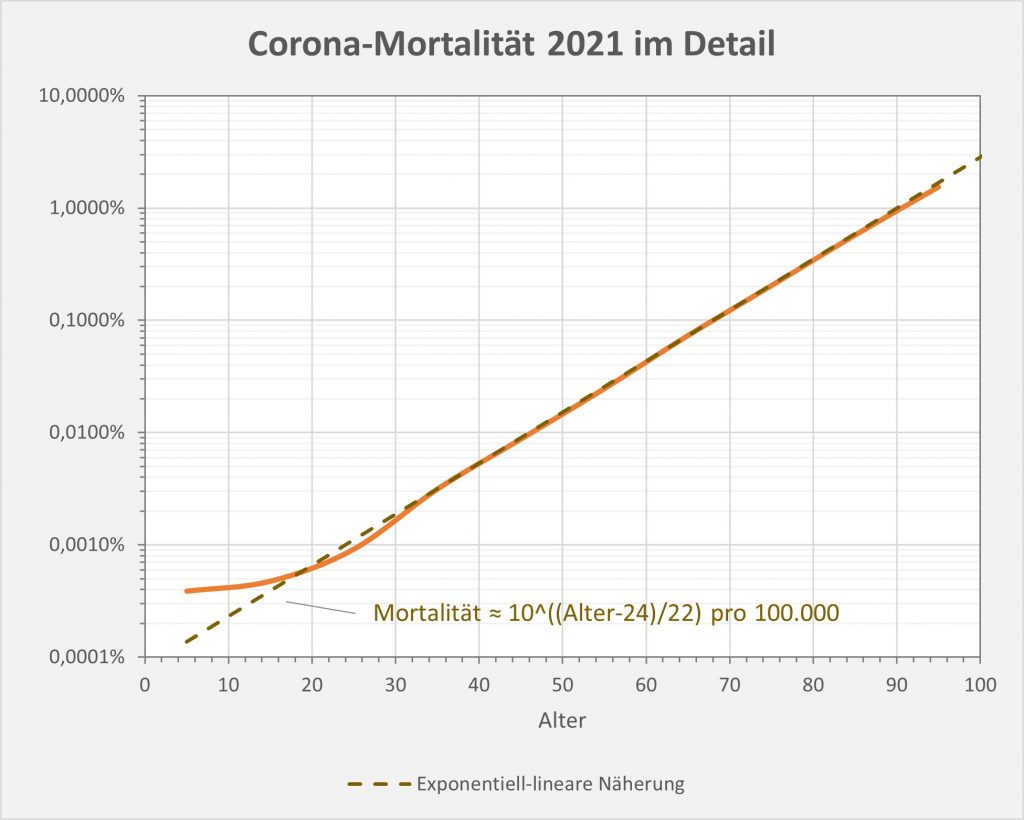
Der vorstehend zusammengefasste Befund ist das Resultat der mit zunehmendem Alter ab etwa 60 bis 70 stark anwachsenden mittleren Sterblichkeit. Das allgemeine Sterberisiko steigt mit dem Alter exponentiell, ähnlich wie auch die Corona-Letalität und die Corona-Mortalität. Daher bleibt es nicht aus, dass in der statistischen Vergleichsbetrachtung insbesondere eine große Anzahl der Älteren auch ohne Corona in der definierten Zeitspanne verstorben wäre. Völlig anders würde sich die Situation darstellen, falls die Corona-Sterblichkeit Jüngere in ähnlicher Weise wie Ältere betreffen würde. Wenn wir für einen Augenblick annehmen, die Corona zugeschrieben Todesfälle würden sämtlich in der Altersgruppe unter 60 aufgetreten sein, dann würde die vorstehende statistische Analyse zum Resultat geführt haben, dass 92 % der Fälle, also über 100.000, als zusätzliche und somit mit hoher Wahrscheinlichkeit auf Corona zurückzuführende Sterbefälle zu werten seien.
Gelegentlich wird gegen die obige Argumentation ins Feld geführt, viele der Coronatoten, auch die Älteren, hätten noch eine Lebenserwartung von mehreren Jahren gehabt und seien daher definitiv „an“ und nicht nur „mit“ Corona verstorben. In dieser Pauschalität ist das Unfug, wie man ganz leicht zeigen kann. Es liegt im Wesen einer statistischen Überlegung, nicht vom Einzelfall, sondern von der großen Zahl auszugehen. Betrachten wir exemplarisch die 80-Jährigen. Ihre statistische Lebenserwartung beläuft sich auf ca. 8 Jahre. Das Risiko, in den nächsten 12 Monaten zu versterben liegt aber im Schnitt dennoch bei 5,5 %. Sofern nun eine Person „an oder mit“ Corona verstirbt, scheinen damit zunächst 8 potentielle Lebensjahre vernichtet. Im Einzelfall könnte das auch zutreffen, unter statistischen Gesichtspunkten (also der Heranziehung der großen Zahl) erweist sich dieser Schluss indes als Fehlurteil.
Von 1000 Achtzigjährigen sterben 55 in der statistischen Erwartung innerhalb eines Jahres. Da hilft der Verweis auf die Restlebenserwartung von 8 Jahren nicht weiter. Die Restlebenserwartung ist keinesfalls garantiert, sie ist lediglich eine statistische Kenngröße, genau wie das Sterberisiko. Tatsächlich stehen nicht alle Todesfälle bei 80-Jährigen im Zusammenhang mit Corona, es ist nur etwa jeder zwanzigste Fall. Deswegen ist der Hinweis auf 8 vernichtete Lebensjahre völlig aus der Luft gegriffen. Statistisch darf man allenfalls von einem im Mittel um einige Monate verfrühten Ableben sprechen.
In Summe ist es deswegen eine absolut zulässige Betrachtung, die Corona-Todesfälle im Hinblick auf die bestehende allgemeine Sterbewahrscheinlichkeit zu bewerten. Wie bereits erwähnt, verfährt man im Übrigen betreffend der Verdachtsfälle von Impfungen mit tödlichem Ausgang seitens des PEI in analoger Weise.
Quellen
[1] Paul-Ehrlich-Institut: Corona Sicherheitsbericht für 2021 vom 07.02.2022
[2] Robert Koch-Institut, COVID-19_Todesfälle nach Sterbedatum https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Projekte_RKI/COVID-19_Todesfaelle.html
[3] Robert Koch-Institut, COVID-19_Fälle nach Altersgruppe und Meldedatum
RKI – Coronavirus SARS-CoV-2 – COVID-19-Fälle nach Altersgruppe und Meldewoche (Tabelle wird jeden Donnerstag aktualisiert)
[4] Robert Koch-Institut, Coronavirus Inzidenzen und Impfstatus https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Daten/Inzidenz_Impfstatus.html
[5] Robert Koch-Institut, Coronavirus Fallzahlen https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Daten/Fallzahlen_Kum_Tab.html
[6] Robert Koch-Institut, Coronavirus Impfquotenmonitoring https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Daten/Impfquotenmonitoring.html
[7] Bevölkerung – Zahl der Einwohner in Deutschland nach Altersgruppen am 31. Dezember 2019. Statista
https://de.statista.com/statistik/daten/studie/1112579/umfrage/bevoelkerung-in-deutschland-nach-altersgruppen/
[8] Altersspezifische Sterbewahrscheinlichkeiten der Männer in Deutschland. Bundesinstitut für Bevölkerungsforschung (BIB)
https://www.bib.bund.de/DE/Fakten/Fakt/S05-Altersspezifische-Sterbewahrscheinlichkeiten-Maenner-ab-1871.html?nn=9992070
[9] Altersspezifische Sterbewahrscheinlichkeiten der Frauen in Deutschland. Bundesinstitut für Bevölkerungsforschung (BIB)
https://www.bib.bund.de/DE/Fakten/Fakt/S06-Altersspezifische-Sterbewahrscheinlichkeiten-Frauen-ab-1871.html?nn=9992070
[10] Sterbetafel 2017/2019 – Ergebnisse aus der laufenden Berechnung von Periodensterbetafeln für Deutschland und die Bundesländer 2020. DESTATIS – Statistisches Bundesamt
https://www.destatis.de/DE/Themen/Gesellschaft-Umwelt/Bevoelkerung/Sterbefaelle-Lebenserwartung/Publikationen/Downloads-Sterbefaelle/periodensterbetafel-erlaeuterung-5126203197004.pdf?__blob=publicationFile
[11] Anzahl der Sterbefälle in Deutschland nach Altersgruppe im Jahr 2018. Statista
https://de.statista.com/statistik/daten/studie/1013307/umfrage/sterbefaelle-in-deutschland-nach-alter/
[12] Tabelle: Lebenserwartung (Männer) – in Jahren
https://www.deutschlandinzahlen.de/tab/deutschland/demografie/natuerliche-bevoelkerungsbewegungen/lebenserwartung-maenner
[13] Tabelle: Lebenserwartung (Frauen) – in Jahren
https://www.deutschlandinzahlen.de/tab/deutschland/demografie/natuerliche-bevoelkerungsbewegungen/lebenserwartung-frauen
[14] Corona-Statistik 2020/2021 – sumymus blog
[15] Der Effekt der Corona-Impfung auf die Fallzahlen – sumymus blog
[16] BKK schlägt Alarm: Impf-Nebenwirkungen total unterschätzt | Nordkurier.de
[17] Corona-Impfungen: Fragezeichen beim mRNA-Impfstoff – WELT