Ist die Pandemie nach der Impfkampagne beendet?
Mit zunehmender Dauer der Corona-Pandemie kommt immer mehr die Frage nach der sogenannten Herdenimmunität auf. Wann endlich sind so viele geimpft bzw. von der Infektion genesen, dass eine weitere Ausbreitung des Virus ausgeschlossen werden kann? Oft werden für die Herdenimmunität Zahlen von 60 %, 67 % oder 70 % genannt. Doch gibt es eine Grenze bezüglich der Anzahl der Genesenen bzw. Geimpften, ab welcher keine Infektionsgefahr mehr besteht? Ist die Herdenimmunität eine scharfe epidemiologische Grenze? Kommt es zu keinen weiteren Neuinfektionen mehr, wenn 70 % oder 80 % geimpft sind?
Dazu später. Zunächst wollen wir die Zusammenhänge beleuchten und die Größe der Herdenimmunität ableiten.
Wie breitet sich das Virus aus?
Sei die Größe der Population. Der Wert
steht für die Wahrscheinlichkeit, dass beim Kontakt mit einem Virusträger eine Übertragung stattfindet (was nur innerhalb der begrenzten Infektionszeit von ca. 7 bis 14 Tagen möglich ist). Ferner sei
die durchschnittliche Anzahl der Kontaktpersonen und
die durchschnittliche Anzahl der nicht infizierten Kontaktpersonen eines Erkrankten. Die Anzahl der Neuinfizierten im Intervall bezeichnen wir mit
. Die Gesamtanzahl aller bis zum Intervall
bereits Erkrankten in der Population nennen wir
. Es gilt
.
Für die Anzahl der Neuinfizierten im Intervall erhalten wir nun:
(1)
Wie kommen wir hierin zum Wert von ? Ganz einfach: Die Wahrscheinlichkeit dafür, dass eine zufällig aus der Gesamtpopulation gewählte Kontaktperson noch nicht infiziert ist, können wir leicht bestimmen. Es ist der Quotient
. Demnach gilt
(2)
Zusammengefasst erhalten wir also
(3)
Das Produkt aus Kontaktanzahl und Infektionswahrscheinlichkeit wird oft auch als Reproduktionsfaktor oder R-Wert bezeichnet. Damit erhalten wir die Entwicklungsformel
(4)
Bestimmung der Herdenimmunität
Mittels des Modells kann man leicht bestimmen, welche Bedingung erfüllt sein muss, damit die Anzahl der Neuinfektionen ab einem bestimmten Zeitintervall nicht weiter ansteigt. Dies ist dann der Fall, wenn ist, wenn also gilt,
. Daher lautet die Bedingung
(5)
Wenn also der relative Anteil der Genesenen (bzw. Geimpften, also der Immunisierten) an der Gesamtpopulation erstmals den Wert
übersteigt, gehen die Neuinfektionen zurück. Diese Grenze markiert den Wert der sogenannten Herdenimmunität
und es gilt demnach
(6)
In Abb. 1 ist der Zusammenhang zwischen und
grafisch dargestellt.
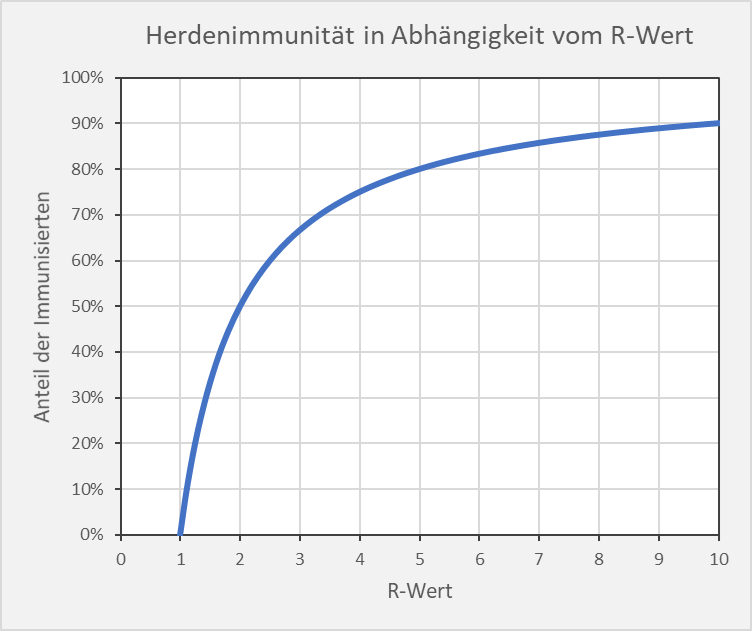
Abbildung 1: Theoretische Herdenimmunität in Abhängigkeit vom Reproduktionsfaktor (R-Wert).
Mathematisch gesehen bestimmt das Maximum im Kurvenverlauf der Neuinfektionen. Wenn der Anteil der Infizierten unterhalb der Grenze
liegt, dann steigen die Neuinfektionszahlen exponentiell, liegt sie oberhalb, dann fallen sie exponentiell.
ist damit zugleich der Wendepunkt im Kurvenverlauf der Gesamtanzahl der Infizierten: Wenn der Anteil der Infizierten
ist, wachsen die Infektionszahlen immer schneller an. Sobald die Grenze
überschritten wird, steigen die Infektionszahlen zwar immer noch, aber der Verlauf wird immer flacher: Es gibt kein exponentielles Wachstum mehr.
Der Wert von definiert also die Grenze, ab welcher die exponentielle Ausbreitung des Virus bei einem gegebenen Reproduktionsfaktor
eingedämmt ist. Das Virus kann sich immer noch ausbreiten, dies vollzieht sich aber mit reduzierter Dynamik. Neuinfektionen in großer Anzahl sind indessen keineswegs ausgeschlossen.
Der Terminus Herden-Immunität ist insofern missverständlich, genaugenommen sogar falsch, da es in der Herde auch dann noch Neuinfektionen geben wird, wenn der Anteil der Genesenen und Geimpften den theoretischen Grenzwert der Herdenimmunität überschreitet. Mit anderen Worten: Die Herde als Ganzes ist NICHT immun, so lange nicht ALLE Herdenmitglieder immun sind. Der Begriff der Immunität bei einer Einzelperson ist demnach nicht übertragbar auf die Immunität der Gesellschaft als Ganzes.
Exemplarische Entwicklung der Infektionszahlen
Die prinzipiellen Zusammenhänge für einen Reproduktionsfaktor (entsprechend einer Herdenimmunität von 33 % bzw. 27,5 Mio. Menschen) sind in Abb. 2 visualisiert.
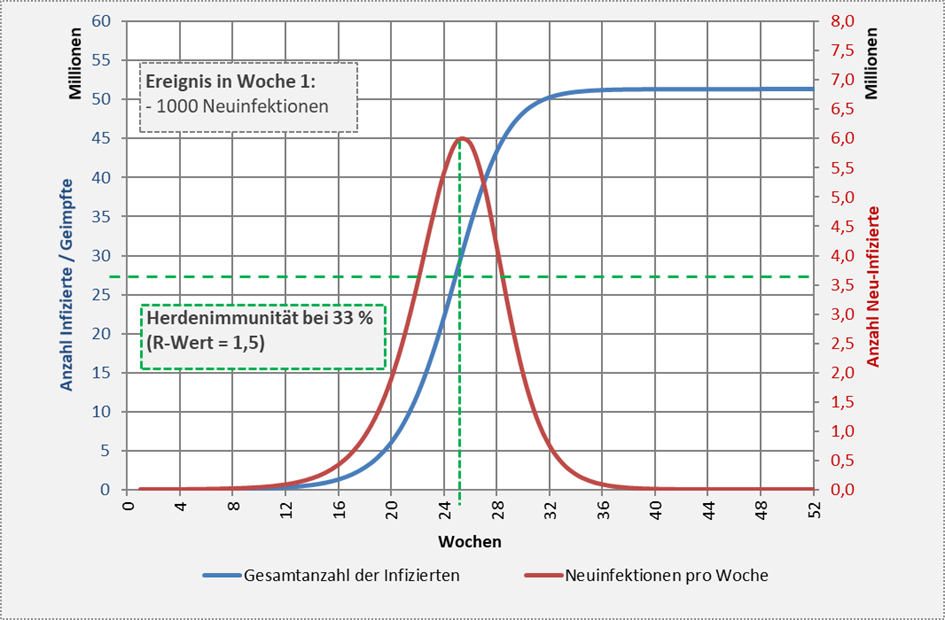
Abbildung 2: Verlauf der Neuinfektionen und der Gesamtanzahl der Immunisierten (hier: Genesene) auf Basis eines Reproduktionsfaktors R = 1,5 unter der Annahme von 1000 Neuinfektionen in der ersten Woche des Betrachtungszeitraums. Dieser R-Wert entspricht einem Wert für die Grenze der Herdenimmunität von 33 % bzw. 27,5 Mio. Menschen (grün gestrichelte horizontale Linie). Der Anteil der Genesenen überschreitet in der 25. Woche die Grenze der Herdenimmunität (grün gestrichelte vertikale Linie). Ab diesem Zeitpunkt geht die Anzahl der Neuinfektionen exponentiell zurück. Die Infektionszahlen steigen aber weiter an und erreichen über 51 Mio. Menschen.
Wie man der vorstehenden Ableitung entnimmt, handelt es sich bei der Herdenimmunität nicht um eine feste Grenze, sondern um einen von der Kontakthäufigkeit und der Infektionswahrscheinlichkeit bzw. vom Reproduktionsfaktor R abhängigen theoretischen Schwellwert.
Wenn der entsprechende Anteil der Population infiziert ist, kommt es zu keinem weiteren exponentiellen Wachstum mehr, vorausgesetzt, die Kontakthäufigkeit und die Infektionswahrscheinlichkeit erhöhen sich nicht. Bei einem Reproduktionsfaktor von 3 (also z.B. durchschnittlich 3 Kontakte mit einer Infektionswahrscheinlichkeit von q=100 %, oder 30 Kontakte mit q=10 %, liegt der Schwellwert für die Herdenimmunität bei exakt 2/3 bzw. 67 %. Erhöht sich aber der R-Wert auf 3,5, so ändert sich der Schwellwert des exponentiellen Wachstums auf 71 %. Bei R-Werten von 4 oder 5 liegt die Grenze entsprechend bei 75 % bzw. 80 %.
Was passiert mit den Infektionszahlen bei einer Erhöhung des R-Wertes?
Wir beleuchten die Fragestellung anhand eines Beispiels. In Abbildung 3 sind die Kurvenverläufe für die Neuinfektionen und die Gesamtanzahl der Infizierten für den exemplarischen Fall der Änderung des R-Wertes von 3 auf 4 aufgetragen. Ausgangsbasis für die Rechnung ist die bereits erreichte Herdenimmunität von 67 % bei einem Reproduktionsfaktor von 3. Es wird angenommen, dass sich der R-Wert in der ersten Woche des Betrachtungszeitraums auf 4 erhöht und zugleich 1000 Neuinfektionen stattfinden. Höhere R-Werte können temporär durchaus entstehen, z.B. aufgrund von Massenveranstaltungen.
Wenn der R-Wert (theoretisch) für 1 Jahr konstant bei 4 bleibt, steigen die Neuinfektionen in der Folge bis zur 30. Woche exponentiell an und erreichen dort ihr Maximum mit fast 1 Mio. Neuinfizierten. Danach nimmt die Anzahl der Neuinfektionen rapide ab und liegt nach einem Jahr wieder auf dem Niveau des Ausgangswertes. Die Gesamtanzahl der Immunisierten (Infizierte bzw. Geimpfte) steigt im gleichen Zeitraum aufgrund der Neuinfektionen von 67 % (ca. 55,6 Mio.) um 12,6 Mio. auf 82 % (68,2 Mio.).
Zwar liegt die Herdenimmunität bei einem R-Wert von 4 nur bei 75 % (62,5 Mio.), dennoch steigt die Gesamtanzahl der Infizierten weit über diese Summe hinaus, weil beim Erreichen der Immunitätsgrenze in der 30. Woche noch Hundertausende Neuinfektionen vorliegen, die über weitere 20 Wochen die Anzahl der Infizierten noch zusätzlich um fast 6 Mio. steigen lassen. In Abb. 3 sind die Zusammenhänge detailliert dargestellt.
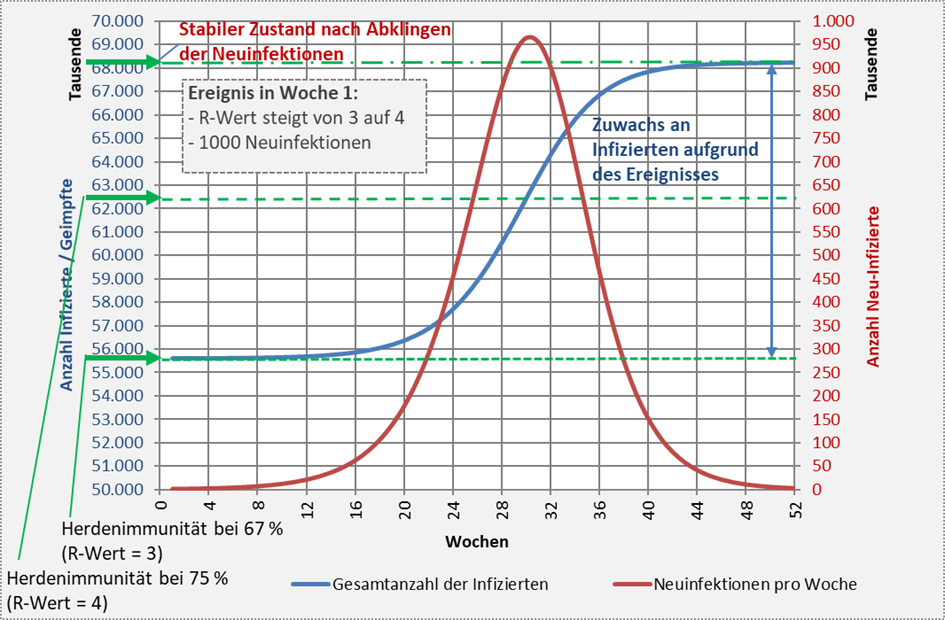
Abbildung 3: Verlauf der Neuinfektionen und der Gesamtanzahl der Immunisierten (Genesene bzw. Geimpfte) ausgehend von einem Immunisierungsgrad von 67 % (entsprechend knapp 56 Mio. Immunisierten). Grundlage für die Modellrechnung sind 1000 Neuinfektionen in der ersten Woche des Betrachtungszeitraums bei einem von 3 auf 4 erhöhten Reproduktionsfaktor. Der Anteil der Genesenen überschreitet in der 30. Woche die Grenze der aus dem R-Wert von 4 resultierenden theoretischen Herdenimmunität von 75 %. Ab diesem Zeitpunkt geht die Anzahl der Neuinfektionen exponentiell zurück. Die Infektionszahlen steigen aber weiter an und erreichen über 68 Mio. Menschen, das sind etwa 12,6 Mio. mehr als zu Beginn des Ausbruchs.
Abschätzung zur Anzahl der Neuinfektionen bei einer Erhöhung des R-Wertes
Wir haben gesehen, dass es bei einer Erhöhung des R-Werts einen Überschwingeffekt gibt. Die Gesamtanzahl der der Immunisierten (Genesene bzw. Geimpfte) klettert bei einem erneuten Ausbruch mit größerem R-Wert aus dem stabilen Zustand mit dem Immunisierungsgrad nicht nur auf den entsprechenden höheren Wert der Herdenimmunität, sondern geht weit darüber hinaus. Die Anzahl der Neuinfizierten
bei ungebremster Infektion mit dem erhöhten R-Wert kann man näherungsweise zu
(7)
bestimmen. Im vorangegangenen Beispiel (s. Abb. 3) kommt man so auf die Abschätzung .
Bestimmung des effektiven R-Wertes
Ausgehend von einer stabilen Situation mit einem Immunisierungsgrad in Höhe der Herdenimmunität verlaufen die Infektionszahlen bei einer Erhöhung des R-Wertes (z.B. von auf
) dem Augenschein nach in etwa so, wie man es in einer Population ohne Immunisierte erwarten würde. Das kann man Abb. 3 unmittelbar entnehmen. Bei genauer Betrachtung erkennt man indes, dass die Geschwindigkeit der Ausbreitung deutlich reduziert ist. Im Ergebnis beobachten wir unmittelbar nach dem Ausbruch ein Wachstum bei der Anzahl der Neuinfektionen mit einem effektiven Reproduktionsfaktor von
(8)
Wenn wir die Fälle mit betrachten (also
), ergibt sich dabei stets ein effektiver R-Wert
(da
), also exponentielles Wachstum. Daher müssen wir immer mit einer exponentiellen Ausbreitung von Neuinfektionen rechnen, sofern der aktuelle Immunisierungsgrad kleiner als die aus dem vorliegenden R-Wert resultierende theoretische Herdenimmunität ist.
In der Situation von Abb. 3 haben wir initial stabile Verhältnisse, da der erreichte Immunisierungsgrad von 67 % dem unterstellten R-Wert von etwa 3 entspricht. Aufgrund der Erhöhung des R-Werts auf 4 führt die induzierte Infektion von 1000 Personen zu einem exponentiellen Anstieg der Neuinfektionen. Der anfängliche effektive Reproduktionsfaktor (R-Wert) beläuft sich hierbei nach obiger Formel auf .
Analyse des Infektionsgeschehens in Abhängigkeit vom Immunisierungsgrad
Nun haben wir oben ein Extrembeispiel betrachtet. In der Realität wird man einen solchen Ausbruch nicht dauerhaft geschehen lassen und Gegenmaßnahmen zur Eindämmung der Ausbreitung ergreifen (Kontaktreduzierung, Impfung). Die Anzahl der Neuinfizierten ist abhängig vom R-Wert, dem jeweils erreichten Immunisierungsgrad (Anteil der Immunisierten in der Population, entweder durch Impfung oder durch Genesung), von der initialen Inzidenz beim erneuten Ausbruch und von der Dauer der Ausbreitung mit dem erhöhten R-Wert.
Zunächst betrachten wir die Abhängigkeit des Infektionsgeschehens vom Immunisierungsgrad (s. Abb. 4).
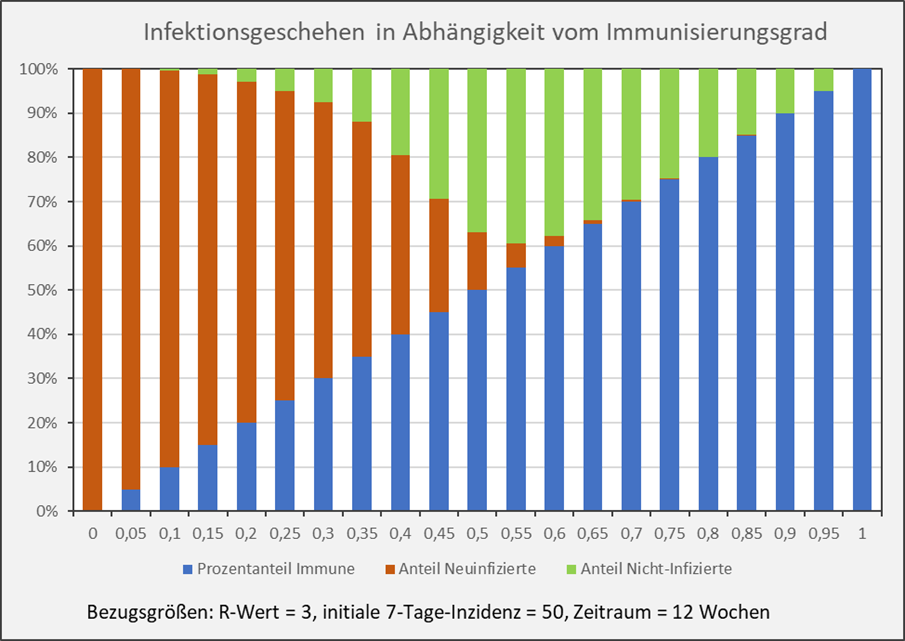
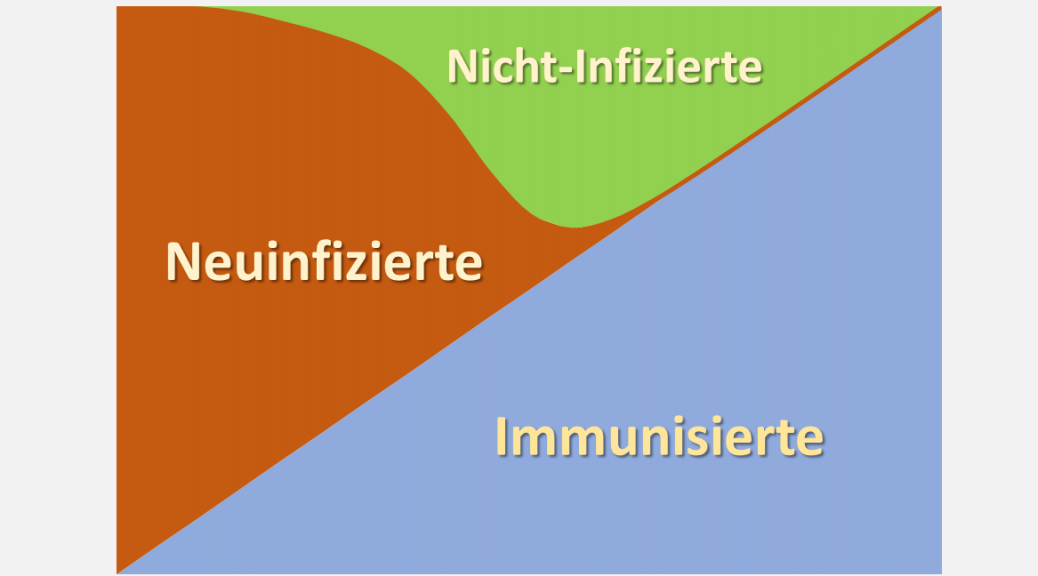
Abbildung 4: Infektionsgeschehen in Abhängigkeit vom Immunisierungsgrad. Blau: Anteil der Immunisierten (Immunisierungsgrad); Rot: Anteil der Neuinfizierten nach einem Ausbruch mit einer initialen 7-Tage-Inzidenz von 50 im Verlauf von 12 Wochen; Grün: Verbleibender Anteil der Nicht-Infizierten. Beispiel: Balken bei x = 0,55: Immunisierungsgrad = 55 % (blaue Säule); Anteil der sich neu Infizierenden im Verlauf der nächsten 12 Wochen = 5 % (rote Säule bei x = 0,55); Anteil der nicht Infizierten im Verlauf der nächsten 12 Wochen = 40 % (grüne Säule bei x = 0,55);
Man entnimmt der Darstellung unmittelbar, dass der Anteil der Neuinfizierten (rote Säulen) bei höheren Immunisierungsgraden sehr schnell geringer wird. Im Beispiel von Abb. 4 ist die rote Säule für Immunisierungsgrade über 70 % im Diagramm nicht mehr erkennbar. Diese 70 % entsprechen in diesem Fall (R = 3) in etwa der theoretischen Herdenimmunität von 67 %.
Der Einfluss des Reproduktionsfaktors
Wie ändert sich nun die Situation bei Variation des R-Werts? Dazu betrachten wir die nachfolgende Abb. 5. Die Kurvenverläufe zeigen für verschiedene R-Werte die Anteile der Neuinfektionen und der Nicht-Infizierten in Abhängigkeit vom Immunisierungsgrad. Exemplarisch wurde eine anfängliche Inzidenz vom 50 Infektionen pro 100.000 Personen zugrunde gelegt und ein Zeitraum von 12 Wochen betrachtet. Man sieht, wie stark der R-Wert in das Verhältnis der Anteile von Immunisierten, Neuinfizierten und Nicht-Infizierten eingeht.
Beispiele: R-Wert = 2,5 (orangefarbene Kurve): Immunisierungsgrad = 0,3 (30 %), Neuinfizierte = 40 % (= 70 % – 30 %), Nicht-Infizierte = 30 % (= 100 % – 70 %); R-Wert = 3 (braune Kurve): Immunisierungsgrad = 0,3 (30 %), Neuinfizierte = 62 % (= 92 % – 30 %), Nicht-Infizierte = 8 % (= 100 % – 92 %); R-Wert = 5 (hellrote Kurve): Immunisierungsgrad = 0,7 (70 %), Neuinfizierte = 10 % (= 80 % – 70 %), Nicht-Infizierte = 20% (= 100 % – 80 %). Der oben bestimmte Wert für die Herdenimmunität ist näherungsweise der Immunisierungsgrad, bei welchem die entsprechende Kurve der Diagonale (grün) nahekommt und sie scheinbar berührt.
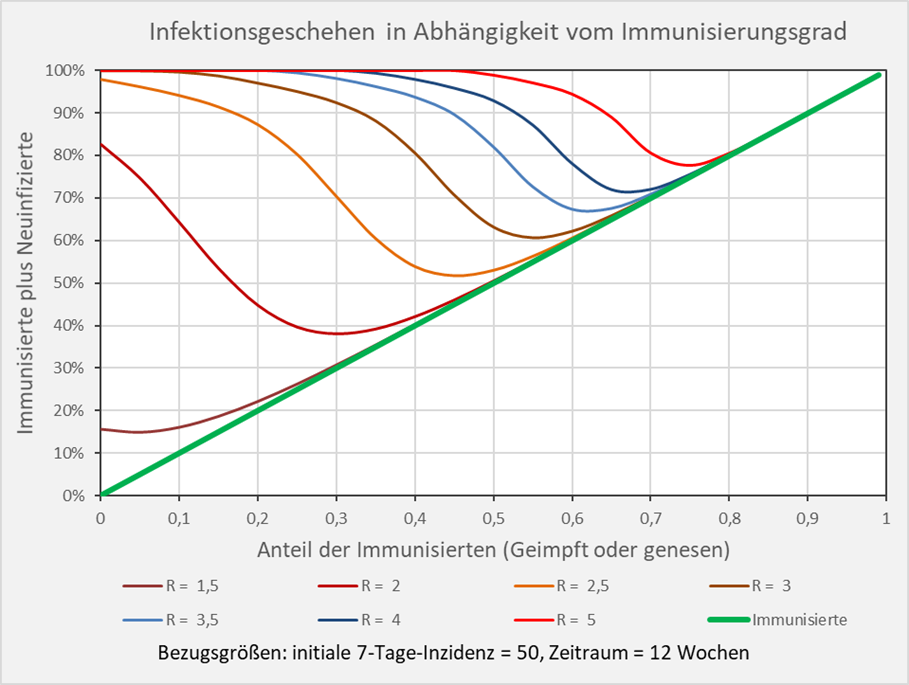
Abbildung 5: Infektionsgeschehen in Abhängigkeit vom Immunisierungsgrad. Die Kurvenverläufe zeigen für verschiedene R-Werte die Anteile der Neuinfektionen und der Nicht-Infizierten in Abhängigkeit vom Immunisierungsgrad. Näherungsweise ist die Herdenimmunität der Immunisierungsgrad, bei welchem die entsprechende Kurve der Diagonale (grün) nahekommt und sie scheinbar berührt. Beispiel: R-Wert = 5 (hellrote Kurve): Immunisierungsgrad = 0,7 (70 %), Neuinfizierte = 10 % (= 80 % – 70 %), Nicht-Infizierte = 20 % (= 100 % – 80 %).
Im vorstehenden Diagramm sind die 3 relevanten Informationen: Immunisierungsgrad, Anteile der Neuinfektionen und Anteil der Nicht-Infizierten in ihrer relativen Größe zueinander dargestellt. Interessiert sind wir indes vor allem am Anteil der resultierenden Neuinfektionen nach einem Ausbruch bei gegebenem Immunisierungsgrad. Diese Info findet sich für dieselbe Parameterkonfiguration unmittelbar in Abb. 6.
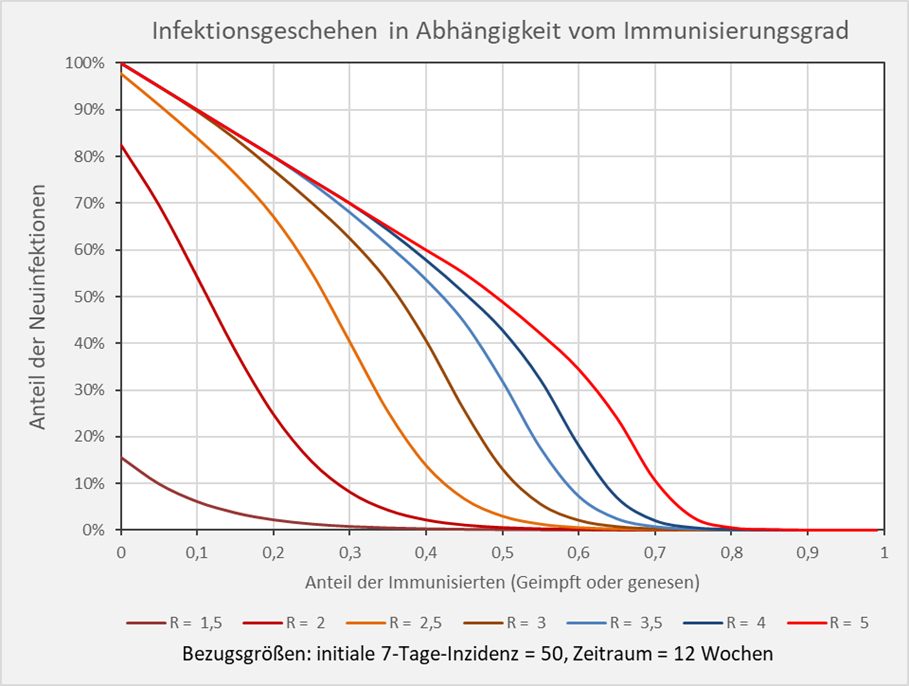
Abbildung 6: Infektionsgeschehen in Abhängigkeit vom Immunisierungsgrad. Bezugsgrößen: initiale 7-Tage-Inzidenz = 50, Zeitraum = 12 Wochen. Die Kurvenverläufe zeigen für verschiedene R-Werte die Anteile der Neuinfektionen in Abhängigkeit vom Immunisierungsgrad. Beispiel: R-Wert = 5 (hellrote Kurve): Immunisierungsgrad = 0,7 (70 %), Neuinfizierte = 10 % der Gesamtbevölkerung.
Infektionsgeschehen bei Immunisierungsgraden in der Nähe der Herdenimmunität
Grundsätzlich erkennt man anhand der Kurvenverläufe in Abb. 6, dass die relativen Neuinfektionszahlen mit wachsendem Immunisierungsgrade sehr schnell kleiner werden. Allerdings verflachen sich die Kurven bei höheren Immunisierungsgraden in der Nähe der theoretischen Herdenimmunität (z.B. 80 % bei R = 5, hellrote Kurve). Um die Verläufe in diesem Bereich sichtbar zu machen, sind die relativen Anteile der Neuinfektionszahlen im Folgenden in logarithmischer Skalierung aufgetragen. Die Reduzierung der Anzahl der Neuinfektionen durch Erhöhung des Immunisierungsgrades ist nun direkt ablesbar.
Beispiel: Bei einem R-Wert von 1,5 und einem Immunisierungsgrad von 0,55 (55 %) entnehmen wir der Grafik einen Wert von 0,1% Neuinfektionen binnen 12 Wochen nach einem Ausbruch mit der anfänglichen Inzidenz von 50 pro 100. 000 Einwohner (s. Abb. 7). Dagegen sind es bei einem R-Wert von 3 im selben Zeitraum bereits 6 % Neuinfektionen bezogen auf die Gesamtbevölkerung.
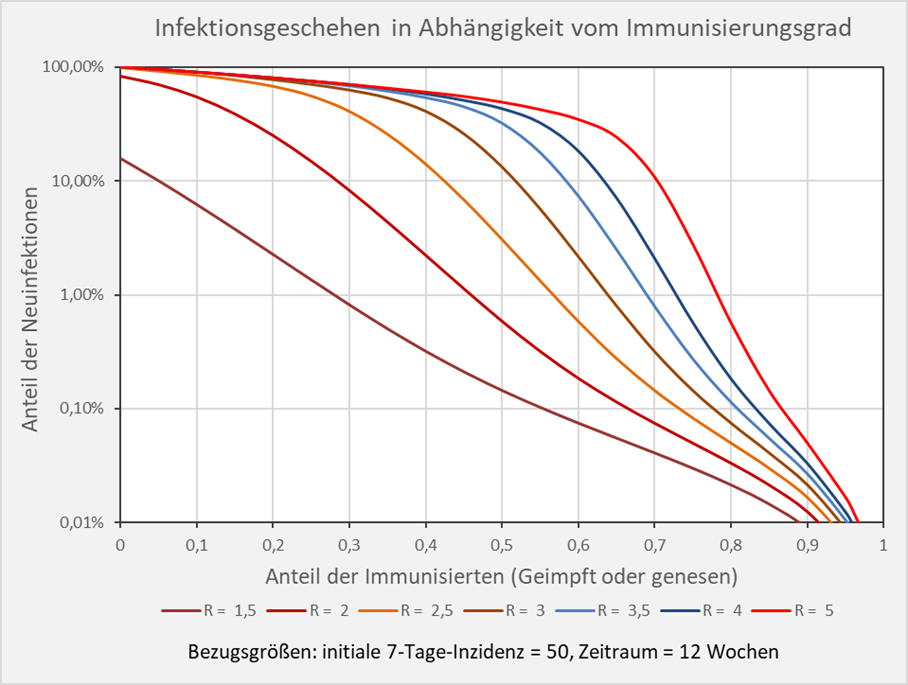
Abbildung 7: Infektionsgeschehen in Abhängigkeit vom Immunisierungsgrad in logarithmischer Skalierung. Bezugsgrößen: initiale 7-Tage-Inzidenz = 50, Zeitraum = 12 Wochen. Die Kurvenverläufe zeigen für verschiedene R-Werte die Anteile der Neuinfektionen in Abhängigkeit vom Immunisierungsgrad. Beispiel: R-Wert = 5 (hellrote Kurve): Immunisierungsgrad = 0,7 (70 %), Neuinfizierte = 10 % der Gesamtbevölkerung.
Sensitivitätsanalyse
Bei höheren Inzidenzen verschieben sich die Kurven nach rechts, so dass die die Anzahl der Neuinfektionen nach einem neuerlichen Ausbruch steigt. Bei der gegenüber dem Beispiel oben verdoppelten Inzidenz von 100 pro 100. 000 Einwohnern sind es nun für den R-Wert 1,5 und einem Immunisierungsgrad von 0,55 (55 %) 0,2 % Neuinfektionen binnen 12 Wochen, und bei einem R-Wert von 3 im selben Zeitraum bereits 10 % Neuinfektionen bezogen auf die Gesamtbevölkerung (s. Abb. 8).
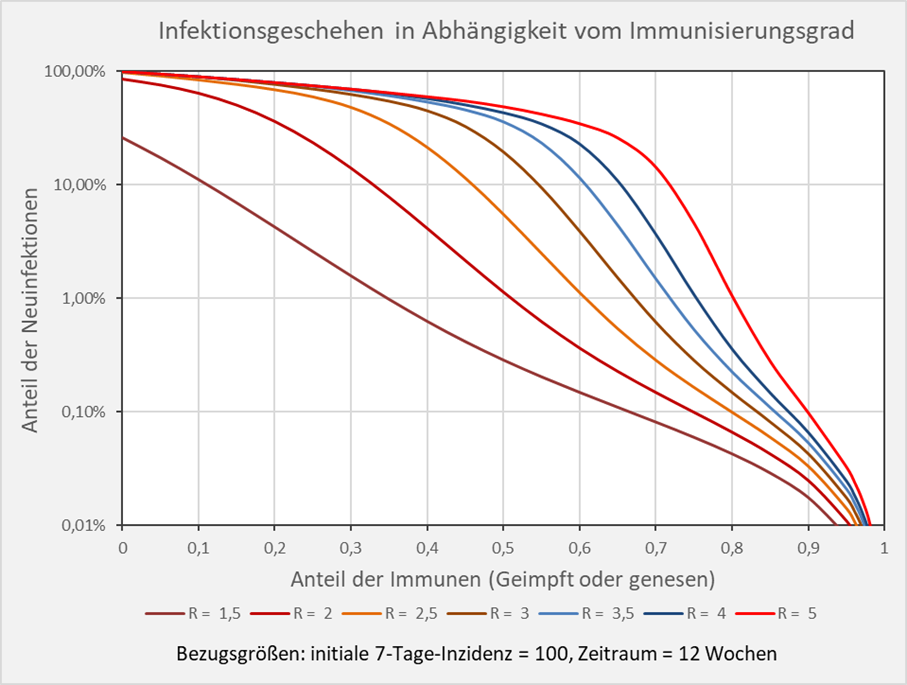
Abbildung 8: Infektionsgeschehen in Abhängigkeit vom Immunisierungsgrad in logarithmischer Skalierung. Bezugsgrößen: initiale 7-Tage-Inzidenz = 100, Zeitraum = 12 Wochen. Die Kurvenverläufe zeigen für verschiedene R-Werte die Anteile der Neuinfektionen in Abhängigkeit vom Immunisierungsgrad. Beispiel: R-Wert = 5 (hellrote Kurve): Immunisierungsgrad = 0,7 (70 %), Neuinfizierte = 16 % der Gesamtbevölkerung; Immunisierungsgrad = 0,8 (80 %), Neuinfizierte = 1 % der Gesamtbevölkerung.
Der einem Neuinfektionsanteil von 1 % entsprechende Immunisierungsgrad stimmt bei einer angenommenen Inzidenz von 100 und einem Betrachtungszeitraum von 12 Wochen in guter Näherung mit dem Wert der theoretischen Herdenimmunität überein (vgl. Abb. 1 und Abb. 8). D. h., sofern der Immunisierungsgrad der Population in etwa dem Wert für die Herdenimmunität entspricht, infizieren sich bei einem Ausbruch mit der Inzidenz 100 binnen 12 Wochen ca. 1 % der Bevölkerung.
Erweitern wir nun die summarische Sensitivitätsanalyse in Richtung der Verlängerung des Betrachtungszeitraums. In erster Näherung nimmt man ähnliche Veränderungen wahr, wie bei einer entsprechenden Vergrößerung der Inzidenz. In Abb. A-1 (s. Anhang) ist die Kurvenschar auf Basis einer initialen 7-Tage-Inzidenz von 50 und einer Dauer von 24 Wochen dargestellt. Im Vergleich zur Situation bei der halben Dauer von 12 Wochen, sind die Infektionszahlen bei niedrigen Immunisierungsgraden deutlich erhöht. Dagegen steigen bei die Infektionszahlen bei hohen Immunisierungsgraden merklich geringer.
Beispiel: R-Wert = 2 (rote Kurve): Immunisierungsgrad = 0,4 (40 %), Neuinfizierte = 2 % der Gesamtbevölkerung bei einer Dauer von 12 Wochen (s. Abb. 7), aber Neuinfizierte = 10 % bei einer Dauer von 24 Wochen. R-Wert = 2,5 (orange Kurve): Immunisierungsgrad = 0,6 (60 %), Neuinfizierte = 0,6 % der Gesamtbevölkerung bei einer Dauer von 12 Wochen (s. Abb. 7), aber Neuinfizierte = 1 % bei einer Dauer von 24 Wochen.
Absolute Infektionszahlen in Abhängigkeit vom Immunisierungsgrad
Im Folgenden bestimmen wir die Höhe der absoluten Infektionszahlen bei gegebenen Immunisierungsgraden und den initialen 7-Tage-Inzidenzen von 50 und 100 sowie den Betrachtungszeiträumen 12 und 24 Wochen.
„Normales“ Leben führt zu R-Werten zwischen 2 und 3 für Personen mit eher geringer Kontakthäufigkeit und R-Werten zwischen 3 und 4 für Personen mit höherer Kontakthäufigkeit und -intensität. Betreffend Massenveranstaltungen muss man teilweise mit Reproduktionsfaktoren deutlich darüber rechnen (bis zu 5, evtl. auch mehr).
Wir beschränken uns daher auf Reproduktionsfaktoren R = 2 bis 5 und Immunisierungsgrade 50 % bis 80 %. Bei niedrigeren Immunisierungsgraden gehen die Neuinfektionszahlen unter den gegebenen Randbedingungen schnell in die Millionen. Umgekehrt erscheinen Immunisierungsgrade über 80 % in absehbarer Zeit kaum erreichbar.
Die Ergebnisse sind in den Abbildungen 9 und 10 zusammengetragen. Die weitere Sensitivitätsanalyse findet sich im Anhang (s. Abb. A-2 und A-3 sowie Abb. A-4 und A-5).
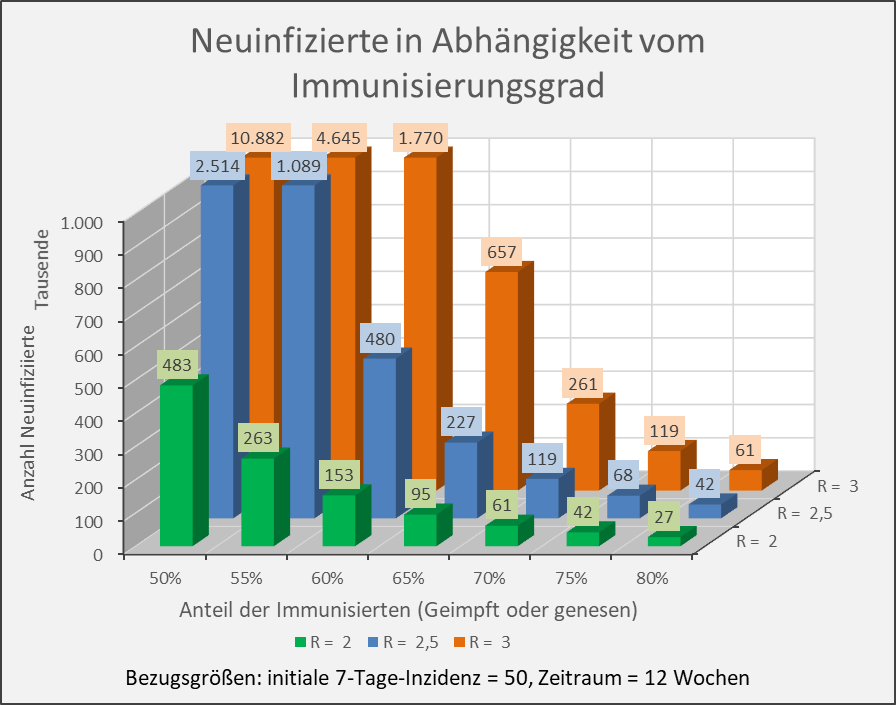
Abbildung 9: Neuinfizierte in Abhängigkeit vom Immunisierungsgrad für R-Werte 2, 2,5 und 3. Bezugsgrößen: initiale 7-Tage-Inzidenz = 50, Zeitraum = 12 Wochen. Die Säulen zeigen jeweils die Anzahl der Neuinfektionen für die entsprechenden Wertekombinationen von Immunisierungsgrad und R-Wert. Beispiel: R-Wert = 2,5 (blaue Säulen), Immunisierungsgrad = 60 %, Neuinfizierte = 480.000 innerhalb von 12 Wochen.
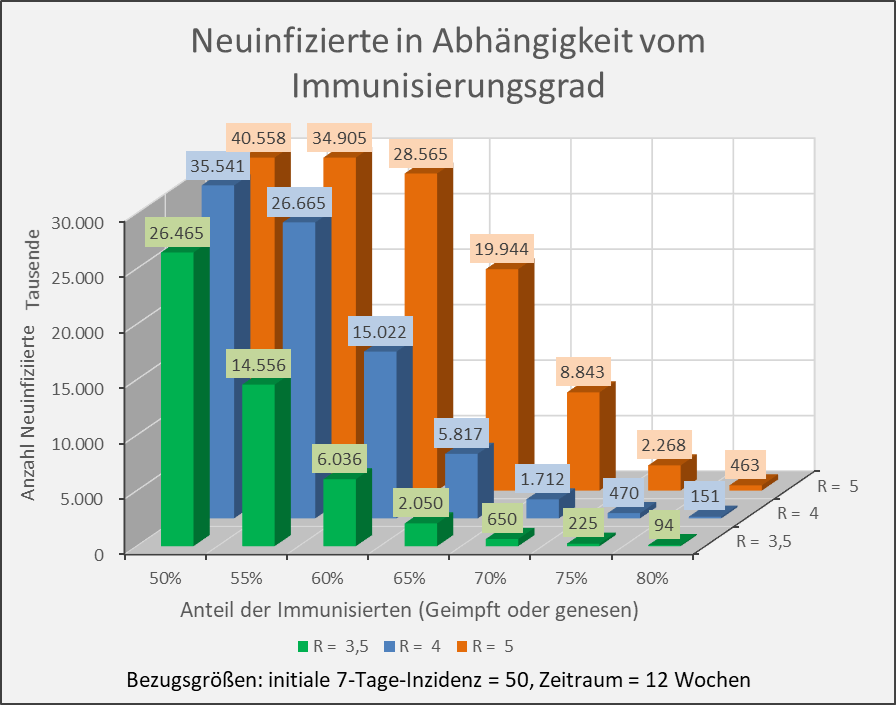
Abbildung 10: Neuinfizierte in Abhängigkeit vom Immunisierungsgrad für R-Werte 3,5, 4 und 5. Bezugsgrößen: initiale 7-Tage-Inzidenz = 50, Zeitraum = 12 Wochen. Die Säulen zeigen jeweils die Anzahl der Neuinfektionen für die entsprechenden Wertekombinationen von Immunisierungsgrad und R-Wert. Beispiel: R-Wert = 3,5 (grüne Säulen), Immunisierungsgrad = 60 %, Neuinfizierte = 6 Mio. innerhalb von 12 Wochen.
Die vorstehenden Abbildungen zeigen, dass es nicht ausreicht, einfach nur einen Immunisierungsgrad in Höhe der formalen Herdenimmunität anzustreben. Auch dann, wenn z.B. 70 % der Menschen immun sind, führt ein neuerlicher Ausbruch mit einem R-Wert von 3,5, aus einer anfänglichen 7-Tage-Inzidenz von 50 Infektionen pro 100.000 Einwohnern (das wären bundesweit 41.500 Infizierte in 7 Tagen) bereits in 12 Wochen zu 650.000 Neuinfektionen, bei einem R-Wert von 4 gar zu 1,7 Millionen (s. Abb. 10).
Zusammenspiel von R-Wert und Immunisierungsgrad
Es stellt sich die Frage, welche Immunisierungsgrade für die Wiedererlangung unserer gewohnten wirtschaftlichen und gesellschaftlich-kulturellen Freiheiten tatsächlich erreicht werden müssen. Werfen wir dazu einen Blick auf Abb. 11. Diese Darstellung dient uns im Folgenden zur Orientierung. Für jedes Wertepaar von R-Wert (0 – 10) und Immunisierungsgrad finden wir hier die grundlegende Information zur Kritikalität der Wertekombination.
Bei den Wertepaaren innerhalb der rot eingefärbten Fläche breitet sich das Virus nach einer anfänglichen Infektion stets mit exponentieller Geschwindigkeit aus. Der grüne Bereich steht für die Kontrolle über das Infektionsgeschehen, da hier umgekehrt jede Infektion rasch verebbt (exponentielle Reduzierung der Neuinfektionszahlen). Dazwischen liegt ein gelber Bereich mit einem näherungsweise linearen Infektionsgeschehen, d.h., die Anzahl der Neuinfektion bleibt ungefähr konstant. Exakt linear ist das Verhalten auf der blauen Grenzkurve. Im gelben Bereich oberhalb und links davon sinken die Neuinfektionszahlen langsam. Unterhalb und rechts davon steigen sie langsam, aber immer mit der Gefahr des Abrutschens in den roten Bereich.
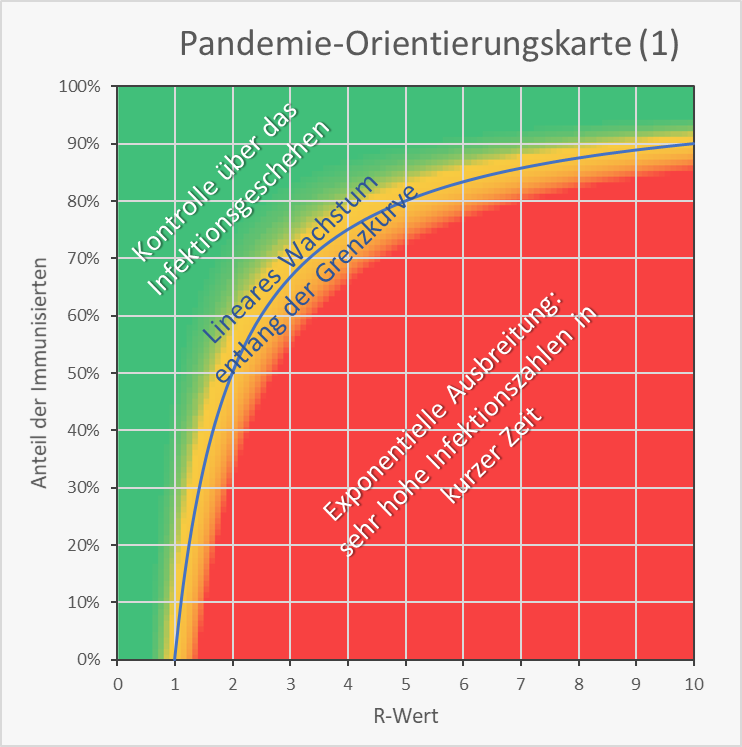
Abbildung 11: Pandemie-Orientierungskarte (1). Kritikalität der Wertekombination von R-Wert (0 – 10) und Immunisierungsgrad (0 – 100).
Realistische Zielsetzung
Nach Abb. 12 verbleibt als realistischer Zielbereich das grün-gelbe Ecksegment zwischen den beiden Verbotszonen und der blauen Grenzkurve. Dabei stellt sich aber die Frage, mit welchem Restrisiko wir rechnen müssen.
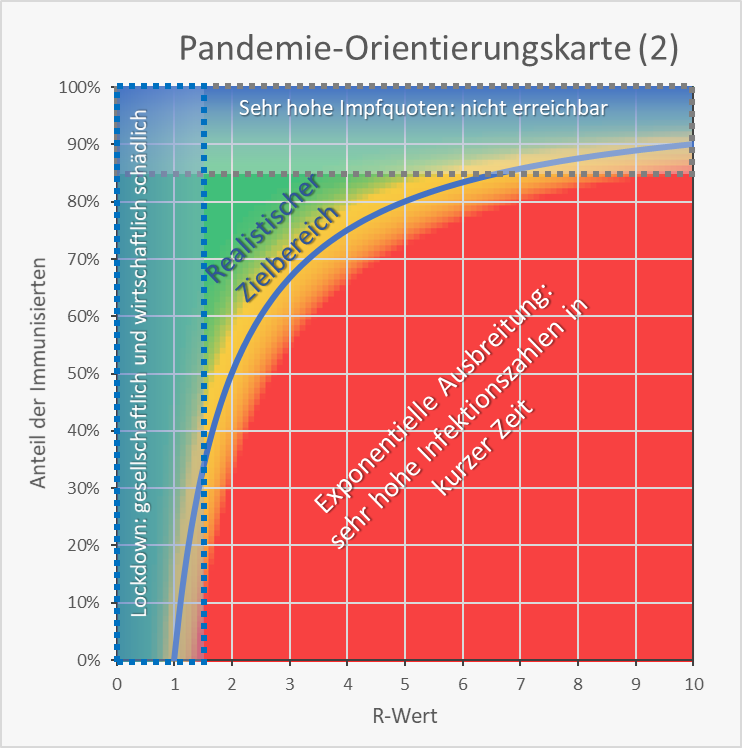
Abbildung 12: Pandemie-Orientierungskarte (2). Kritikalität der Wertekombination von R-Wert (0 – 10) und Immunisierungsgrad (0 – 100). Zusätzlich eingetragen sind die „verbotenen Zonen“: Immunisierungsgrade, die sehr hohe Impfquoten erfordern (blaue Zone im oberen Bereich) sowie R-Werte unter 1,5, die zwar im Lockdown realisierbar sind, aber mit gravierenden gesellschaftlichen und wirtschaftlichen Kollateralschäden einhergehen und ein „normales“ Leben nicht erlauben (blaue Zone im linken Bereich).
Restrisiko
Für einige exemplarische Wertekombinationen von Immunisierungsgrad und R-Wert sind in Abb. 13 die resultierenden Neuinfektionszahlen auf Basis einer initialen 7-Tage-Inzidenz von 50 Neuinfektionen pro 100.000 Einwohner und einer Ausbreitung über 12 Wochen in die Orientierungskarte eingetragen. Man sieht, dass Kombinationen rechts der blauen Grenzkurve zu Neuinfektionszahlen in 7-stelliger Höhe führen. Im grünen Bereich links davon bleibt man im beherrschbaren 5 bis 6-stelligen Bereich. Auf der Grenzkurve selbst ergeben sich binnen 12 Wochen bereits ca. eine halbe Million Neuinfektionen.
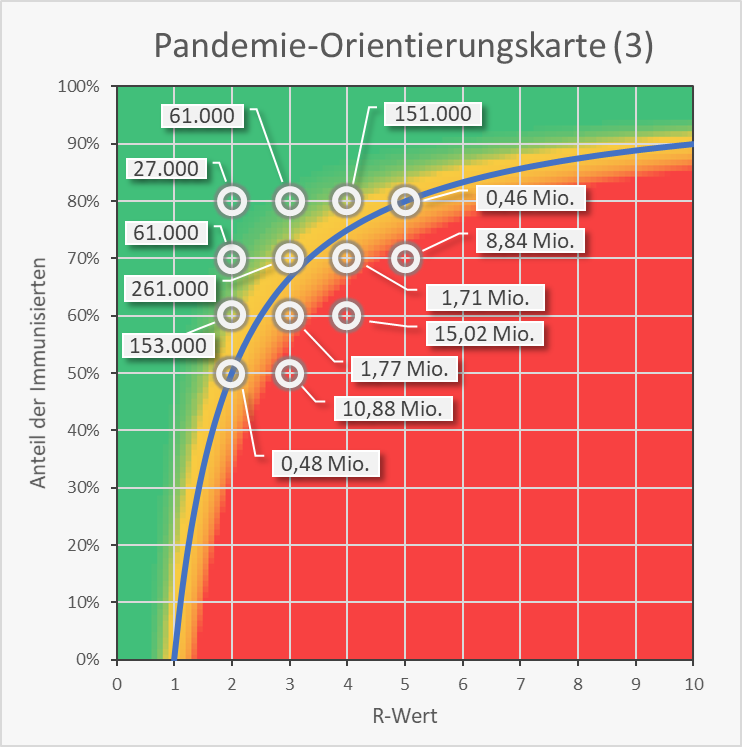
Abbildung 13: Pandemie-Orientierungskarte (3). Kritikalität der Wertekombination von R-Wert (0 – 10) und Immunisierungsgrad (0 – 100). Bezugsgrößen für die Zahlenangaben: initiale 7-Tage-Inzidenz = 50, Zeitraum = 12 Wochen. Rechts der blauen Grenzkurve (exponentielles Wachstum) ergeben sich Neuinfektionszahlen in Millionenhöhe. Links davon bleiben die Neuinfektionszahlen im Bereich von einigen Zehntausend bis einigen Hunderttausend.
Die Zahlenwerte folgen aus den Säulendiagrammen in Abb. 9 und 10. Bei Betrachtung niedriger oder höherer Inzidenzen bzw. von kürzeren oder längeren Ausbreitungszeiten ergeben sich andere Neuinfektionszahlen (s. Abb. A-2 bis A-5 im Anhang), teilweise geringere (niedrigere Inzidenz oder kürzere Ausbreitungsdauer), teilweise aber auch höhere (höhere Inzidenz oder längere Ausbreitungsdauer). Nach der obigen Sensitivitätsanalyse (Abb. 5 – 10 und Anhang) bleibt die Grundaussage indessen dieselbe.
Erhöhtes Risiko, sofern die Impfstoffe nicht zu 100 % wirken
Bei den obigen Rechnungen sind wir von einer 100-prozentigen Wirksamkeit der Impfstoffe ausgegangen und haben unterstellt, dass Geimpfte, 1. immun, und 2. nicht infektiös sind. In welchen Umfang und wie lange das für die einzelnen Impfstoffe und gegen eventuell kursierende Virusmutationen zutrifft, ist gegenwärtig noch weitgehend offen. Wenn z.B. die Immunität effektiv nur bei 90% der Geimpften vorliegt, dann hieße das, dass die Impfquote im Hinblick auf dieselbe Schutzwirkung in der Bevölkerung entsprechend höher sein muss. Um einen effektiven Immunisierungsgrad von 70 % zu erreichen, müssten daher in diesem Falle knapp 78 % der Menschen geimpft werden.
Umgekehrt wären bei einer Impfquote von 70 % effektiv nur 63 % immunisiert. Wie man Abb. 9 entnehmen kann, würde man dann in der Beispielrechnung bei einem R-Wert von 3 statt der 261.000 Infizierten (bezogen auf einen Immunisierungsgrad von 70 %) etwa 1 Mio. Infizierte (bezogen auf einen Immunisierungsgrad von 63 %) bekommen.
Die Sensitivität der Fallzahlen bei Variation des Immunisierungsgrads in Bezug auf den theoretischen Bezugswert der Herdenimmunität ist in Abbildung 14 dargestellt.
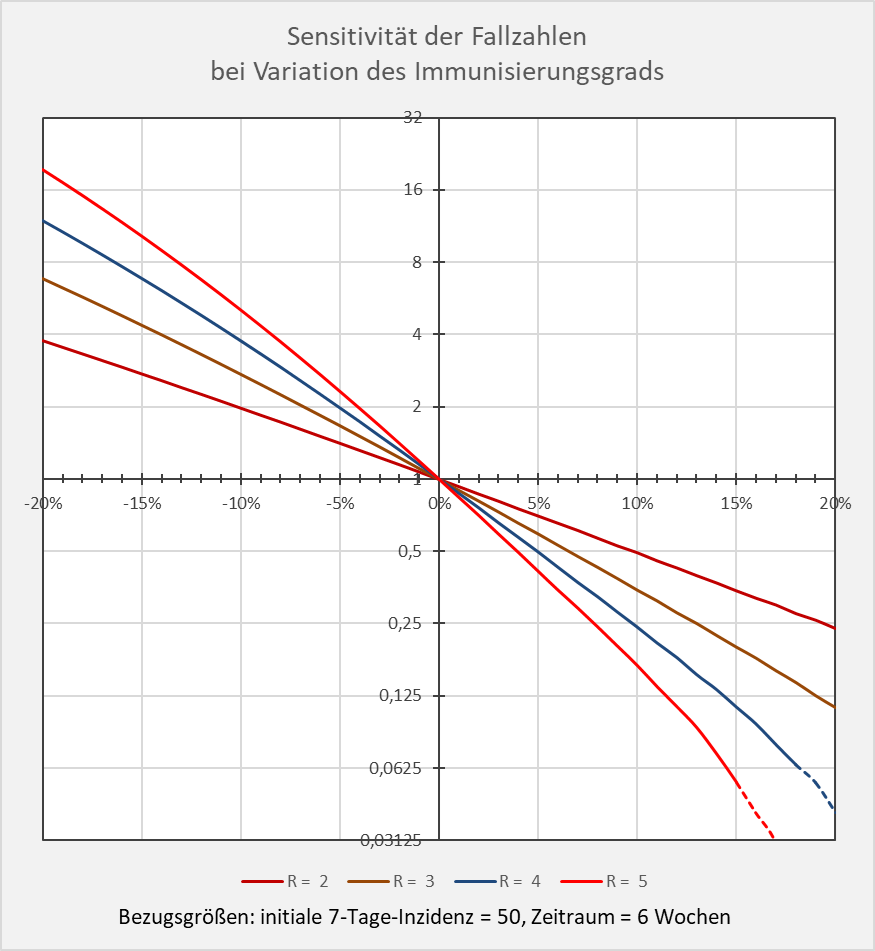
Abbildung 14: Sensitivität der Fallzahlen bei Variation des Immunisierungsgrads. Für unterschiedliche R-Werte ist dargestellt, um welchen Faktor (y-Achse) sich die Neuinfektionszahlen bei einer Änderung des Immunisierungsgrads (x-Achse) im Intervall Herdenimmunität – 20 % bis Herdenimmunität + 20 % verändern. Man beachte die logarithmische Skalierung auf der y-Achse. Bezugswert ist die jeweilige Neuinfektionszahl, die sich bei Übereinstimmung zwischen dem Immunisierungsgrad und der Herdenimmunität ergibt. Bezugsgrößen: initiale 7-Tage-Inzidenz = 50, Zeitraum = 6 Wochen. Beispiel: R-Wert = 4 (blaue Kurve), Immunisierungsgrad = Herdenimmunität – 10 %; dem Diagramm entnimmt man, dass die Anzahl der Neuinfektionen fast 4-mal höher ist als im Falle „Immunisierungsgrad = Herdenimmunität“.
Dem Diagramm kann man unschwer entnehmen, wie sensibel die Fallzahlen auf Abweichungen des effektiven Immunisierungsgrads von der theoretischen Herdenimmunität reagieren. Der Referenzwert im Nullpunkt (also Abweichung = x-Wert = 0 %) ist in Bezug auf den jeweiligen R-Wert auf 1 gesetzt. Die initiale Kurvensteigung im Nullpunkt ist proportional zum R-Wert (genauer: -R).
In der linken Hälfte des Diagramms sieht man, wie stark die Fallzahlen steigen, wenn der Immunisierungsgrad die theoretische Herdenimmunität pro R-Wert um einige Prozentpunkte unterschreitet. Auf der rechten Seite des Diagramms erkennt man umgekehrt, dass die Fallzahlen sehr schnell kleiner werden, sofern der (effektive) Immunisierungsgrad den Wert für die Herdenimmunität nennenswert übersteigt.
Die Kurven in Abb. 14 belegen klar die Kritikalität des Immunisierungsgrads in Bezug auf die aus dem R-Wert bestimmte theoretische Herdenimmunität. Ein effektiver Immunisierungsgrad unterhalb der Herdenimmunität bringt noch keine durchgreifende Entlastung bei den Neuinfektionszahlen. Im Hinblick auf die möglicherweise (bzw. wahrscheinlich) nicht 100%-ige Wirksamkeit von Impfungen muss daher die Impfquote signifikant über der jeweiligen Herdenimmunitätsgrenze liegen.
Folgerungen
Als Resümee aus dem Vorhergehenden ergibt sich die folgende Darstellung (s. Abb. 15): Die Immunisierungsgrade müssen Werte in der oberen Hälfte des eingezeichneten grünen Bereichs annehmen. Je weiter entfernt von der blauen Grenzkurve, desto besser. Bei Immunisierungsgraden unter 70 % sind R-Werte über 3 tabu, da die Infektionszahlen ansonsten binnen weniger Wochen 6-stellig werden können (s. Abb. 13). Umgekehrt erfordern R-Werte um 4 Immunisierungsgrade von 80%.
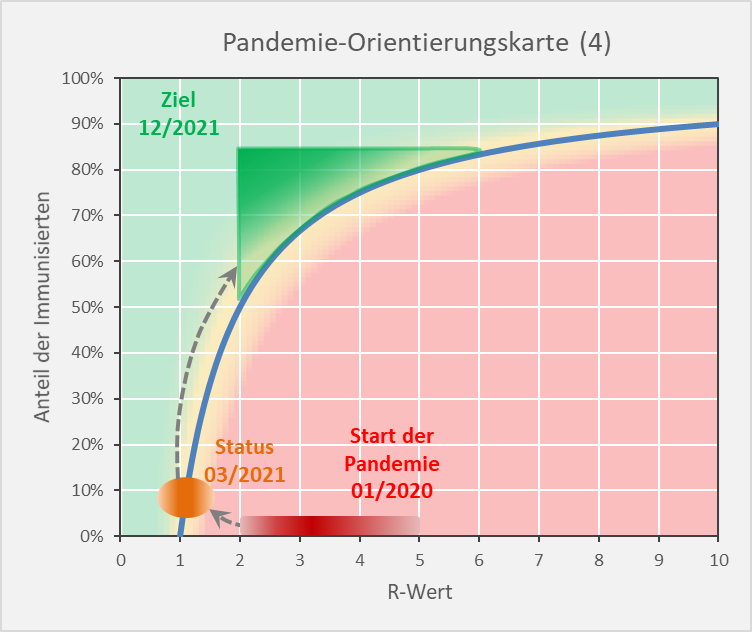
Abbildung 15: Pandemie-Orientierungskarte (4). Ausgangssituation, gegenwärtiger Status und Zielbereich.
In Abbildung 16 sind für die Reproduktionsfaktoren R = 2,5, 3, 4 und 5 jeweils die Werte für die theoretischen Herdenimmunitäten eingetragen. Die grünen Pfeile darüber zeigen die sinnvollen Wertebereiche der dazu passenden Immunisierungsgrade. Nach den vorstehenden Analysen erscheint es zweckmäßig, den Immunisierungsgrad mindestens etwa 5 % über der sich aus dem R-Wert ergebenden theoretischen Herdenimmunität zu wählen. Der entsprechende Bereich ist unten durch die punktierte grüne Line begrenzt. Dies unterstellt, bleiben die Neuinfektionsraten bei der angenommenen initialen Inzidenz von 50 pro 100.000 über einen Zeitraum von 12 Wochen im niedrigen 6-stelligen Bereich (s. Abb. 13), sofern nahezu 100 % der Geimpften tatsächlich immun sind und das Virus nicht weitergeben. Schon wenn die Impfung nur in 1 von 10 Fällen nicht wie erwartet zur Immunisierung führt, was ja immer noch eine hohe Impfwirksamkeit von 90 % wäre, könnten die Neuinfektionen im Betrachtungszeitraum von 12 Wochen die Millionengrenze erreichen und überschreiten.
Nur drei Beispiele dazu: R-Wert = 2,5, Impfquote 60 %, effektive Immunisierung 55 %. Statt der bei einer Immunisierung von 60 % erwarteten Anzahl von 480.000 Neuinfektionen (initiale Inzidenz 50 pro 100.000, 12 Wochen) muss man mit mehr als doppelt so viel rechnen (= 1,09 Mio., vgl. Abb. 9). R-Wert = 3,5, Impfquote 70 %, effektive Immunisierung 65 %. Die bei einer Immunisierung von 70 % erwarteten 650.000 Neuinfektionen (initiale Inzidenz 50 pro 100.000, 12 Wochen) steigen auf die dreifache Anzahl (= 2,05 Mio., vgl. Abb. 10). R-Wert = 4, Impfquote 80 %, effektive Immunisierung 70 %. Gegenüber den bei einer Immunisierung von 80 % zu erwartenden 151.000 Neuinfektionen (initiale Inzidenz 50 pro 100.000, 12 Wochen) könnte sich die Anzahl auf 1,71 Mio. erhöhen (vgl. Abb. 10).
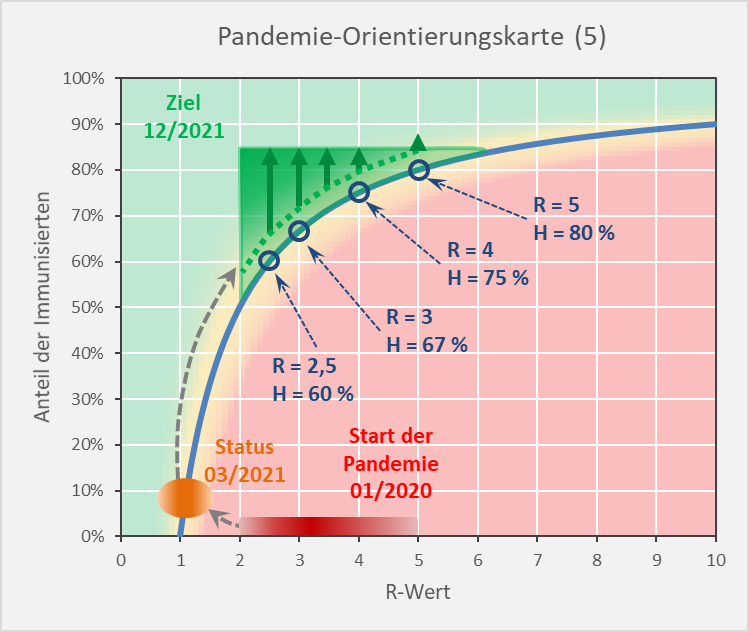
Abbildung 16: Pandemie-Orientierungskarte (5). Ausgangssituation, gegenwärtiger Status und Zielbereich mit den eingezeichneten minimalen Immunisierungsgraden (punktierte Linie / Startpunkte der grünen Pfeile) bezogen auf die Reproduktionsfaktoren R = 2,5, 3, 3,5 und 4 sowie den entsprechenden Herdenimmunitäten H.
Resümee
Nach dem Vorstehenden kann man sich der Erkenntnis nicht verweigern, dass auch bei einer vergleichsweise hohen Impfquote von über 70 % die Pandemie nicht als beendet angesehen werden kann. Unter „normalen“ Bedingungen können die Neuinfektionszahlen selbst bei einem moderaten Ausbruch mit einer 7-Tage-Inzidenz von 50 pro 100.000 Personen in wenigen Wochen Werte von einigen hunderttausend erreichen. Zum Vergleich: In der ersten Corona-Welle waren von Anfang März bis Ende Mai 2020 trotz der Lockdown-Beschränkungen etwa 180.000 Corona-Infektionen zu verzeichnen, und das hat man damals als sehr bedrohlich empfunden. Großveranstaltungen (Sportereignisse, Volksfeste, Karneval, Weihnachtsmärkte) können unter den vor der Pandemie üblichen Bedingungen eine solche Inzidenz fraglos auslösen. Gleichfalls können auch Urlaubsrückkehrer die Quelle für Neuinfektionen sein.
Welchen Schluss kann man daraus ziehen? Impfen bringt nichts? – Keineswegs! Natürlich ist eine hohe Impfquote wichtig, vor allem gilt dies für die vulnerablen Gruppen (insbes. Menschen über 70 oder 80 und Menschen mit Vorerkrankungen). Impfen allein genügt aber nicht. Wir müssen vielmehr lernen, mit dem Corona-Virus zu leben, genau wie wir auch gelernt haben, mit anderen viralen Bedrohungen zurechtzukommen. Diese Aufforderung richtet sich an uns alle, sie geht aber zuvorderst an die verantwortlichen Politiker.
Die Politiker müssen sich der Realität stellen und zu einem wissenschaftlich fundierten, aber eben nicht einseitig am Gesundheitssystem ausgerichteten Krisenmanagement finden. Dazu gehört vor allem die Abkehr von der Inzidenzzahl als dem nahezu einzigen Indikator für die Situationsbeurteilung. Diese Steuergröße ist für die Auslösung von Schutzmaßnahmen denkbar ungeeignet. Ausgehend von der Erwartung, dass die Impfquote in absehbarer Zeit kaum über 70 % steigen wird, legt die vorstehende Analyse nahe, dass die Pandemie noch lange dauern könnte, wenn man ausschließlich auf Inzidenzen schaut.
Es ist nicht die Aufgabe der Politik, jedes Risiko von den Menschen zu nehmen. Und es ist absolut unverhältnismäßig, dem Vorsorgeprinzip alles andere unterzuordnen: Kultur, gesellschaftliche Aktivitäten, Freizeit, ja die gesamte Wirtschaft. Niemand führt Buch über die dergestalt verursachten Kollateralschäden. Freiheitsbeschränkungen sind in der Demokratie höchstens ausnahmsweise und befristet hinnehmbar. Wer das als Politiker anders sieht, sollte sein Amt niederlegen bzw. sich gar nicht erst zur Wahl stellen.
Mündige Staatsbürger brauchen keinen Vormund. Die Eigenverantwortung ist die stärkste Waffe gegen das Corona-Virus. Freiheit und Eigenverantwortung sind die zwei Seiten ein und derselben Medaille. Der Staat trägt Verantwortung nur für diejenigen, die sich nicht selbst schützen können. Darauf muss er sich konzentrieren und soll alles andere der Vernunft, dem Ideenreichtum und dem Gestaltungswillen seiner Staatsbürger überlassen.
Quellen:
[1] Täglicher Lagebericht des RKI zur Coronavirus-Krankheit-2019 (COVID-19) – 23.03.2021 – AKTUALISIERTER STAND FÜR DEUTSCHLAND. RKI
[2] Täglicher Lagebericht des RKI zur Coronavirus-Krankheit-2019 (COVID-19) – 26.01.2021 – AKTUALISIERTER STAND FÜR DEUTSCHLAND. RKI
[3] Corona-Infektionen (COVID-19) in Deutschland nach Altersgruppe und Geschlecht (Stand: 23. März 2021). Statista
[4] Todesfälle mit Coronavirus (COVID-19) in Deutschland nach Alter und Geschlecht (Stand: 23. März 2021). Statista
[5] Nach Krisengipfel: Virologe mit scharfer Corona-Kritik an Merkel und Söder – „Weit weg von Realität“
[6] Corona-Lockdown bis Sommer? Just der Wirtschaftsminister schließt nichts aus
[7] Scharfe Kritik an Corona-Politik und Experten – „Andere Sichtweisen offenbar unerwünscht“
[8] Das „Vorsorgeprinzip“ der Kanzlerin in der Pandemie ist einseitig
[9] Angela Merkel: Unerwarteter Corona-Angriff! Leopoldina attestiert „politischen Missbrauch von Wissenschaft“ | Politik (merkur.de)
[10] NACH DER AUSNAHME KOMMT DIE NORMALITÄT
[11] Das Coronavirus – So schnell breitet es sich aus. Aber wir können etwas tun!
[12] Das Coronavirus: Harmlos? Bedrohlich? Tödlich?
[13] Aktuelles zu Corona
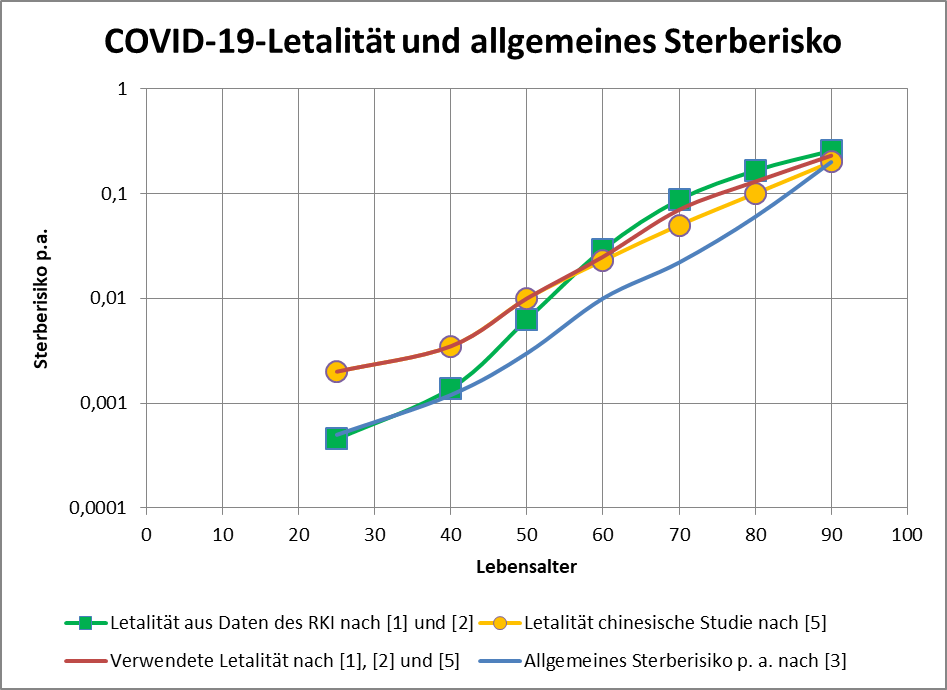
[14] Die Corona-Pandemie: Alter ist der dominierende Risikofaktor
[15] CORONA-KRITIKER AUS DEM ETHIKRAT ENTLASSEN
Anhang:
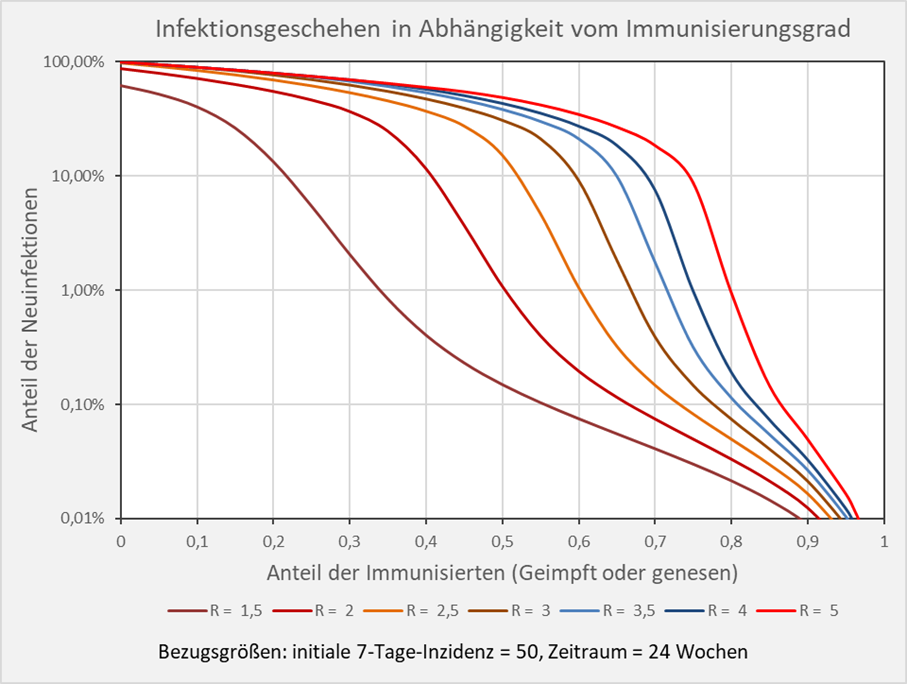
Abbildung A-1: Infektionsgeschehen in Abhängigkeit vom Immunisierungsgrad. Bezugsgrößen: initiale 7-Tage-Inzidenz = 50, Zeitraum = 24 Wochen. Die Kurvenverläufe zeigen für verschiedene R-Werte die Anteile der Neuinfektionen in Abhängigkeit vom Immunisierungsgrad. Beispiel: R-Wert = 5 (hellrote Kurve): Immunisierungsgrad = 0,7 (70 %), Neuinfizierte = 18 % der Gesamtbevölkerung; Immunisierungsgrad = 0,8 (80 %), Neuinfizierte = 1 % der Gesamtbevölkerung.
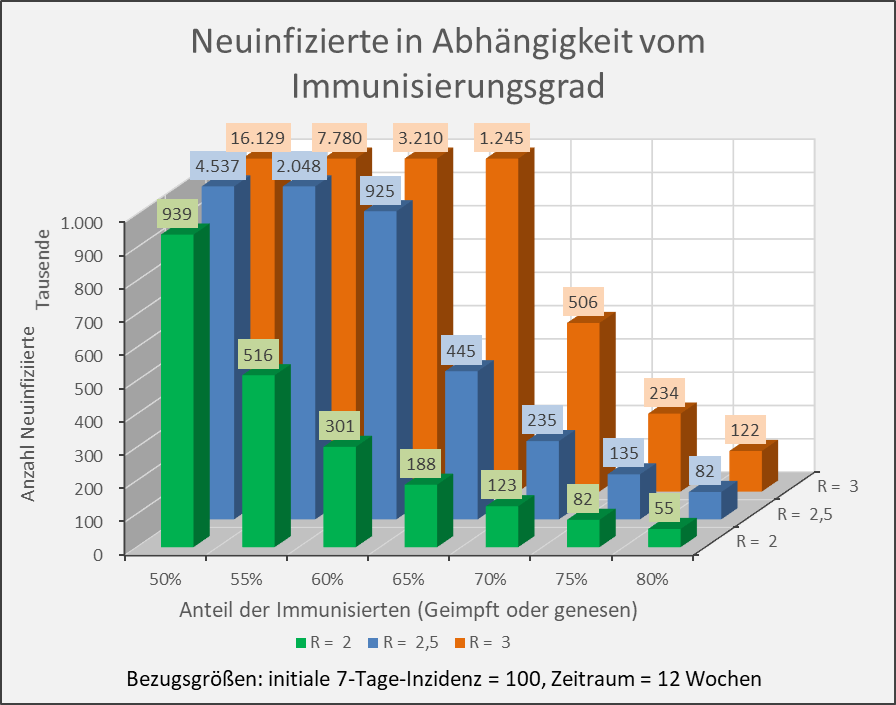
Abbildung A-2: Neuinfizierte in Abhängigkeit vom Immunisierungsgrad für R-Werte 2, 2,5 und 3. Bezugsgrößen: initiale 7-Tage-Inzidenz = 100, Zeitraum = 12 Wochen. Die Säulen zeigen jeweils die Anzahl der Neuinfektionen für die entsprechenden Wertekombinationen von Immunisierungsgrad und R-Wert. Beispiel: R-Wert = 2,5 (blaue Säulen), Immunisierungsgrad = 60 %, Neuinfizierte = 925.000 innerhalb von 12 Wochen.
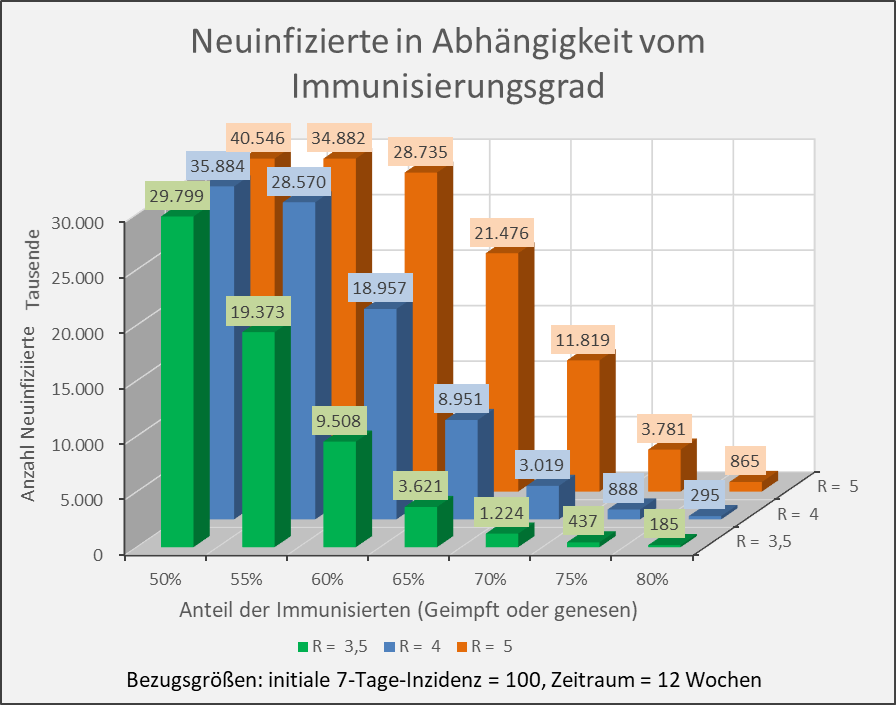
Abbildung A-3: Neuinfizierte in Abhängigkeit vom Immunisierungsgrad für R-Werte 3,5, 4 und 5. Bezugsgrößen: initiale 7-Tage-Inzidenz = 100, Zeitraum = 12 Wochen. Die Säulen zeigen jeweils die Anzahl der Neuinfektionen für die entsprechenden Wertekombinationen von Immunisierungsgrad und R-Wert. Beispiel: R-Wert = 3,5 (grüne Säulen), Immunisierungsgrad = 60 %, Neuinfizierte = 9,5 Mio. innerhalb von 12 Wochen.
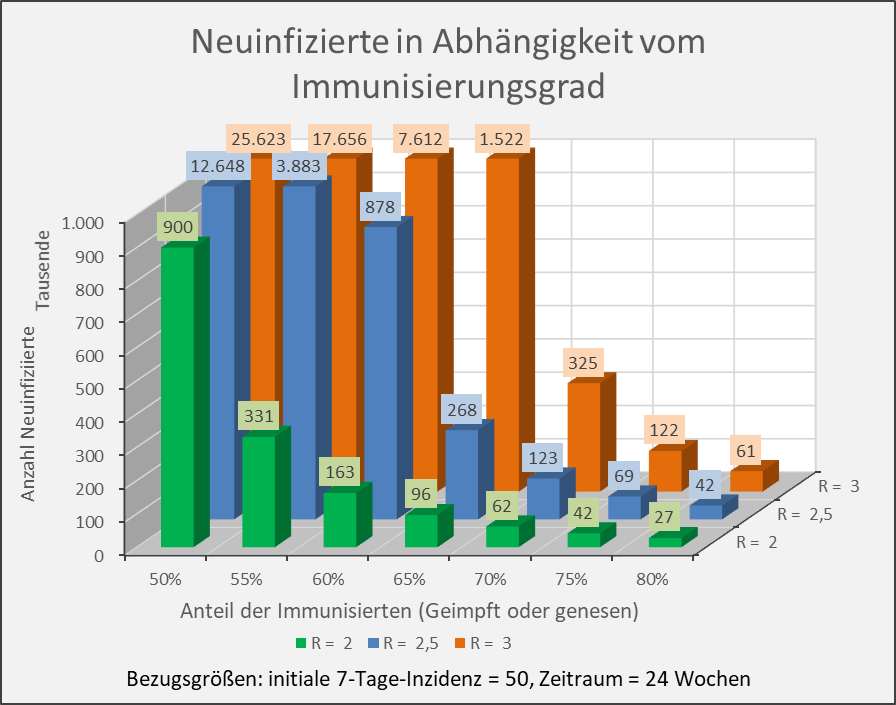
Abbildung A-4: Neuinfizierte in Abhängigkeit vom Immunisierungsgrad für R-Werte 2, 2,5 und 3. Bezugsgrößen: initiale 7-Tage-Inzidenz = 50, Zeitraum = 24 Wochen. Die Säulen zeigen jeweils die Anzahl der Neuinfektionen für die entsprechenden Wertekombinationen von Immunisierungsgrad und R-Wert. Beispiel: R-Wert = 2,5 (blaue Säulen), Immunisierungsgrad = 60 %, Neuinfizierte = 878.000 innerhalb von 24 Wochen.
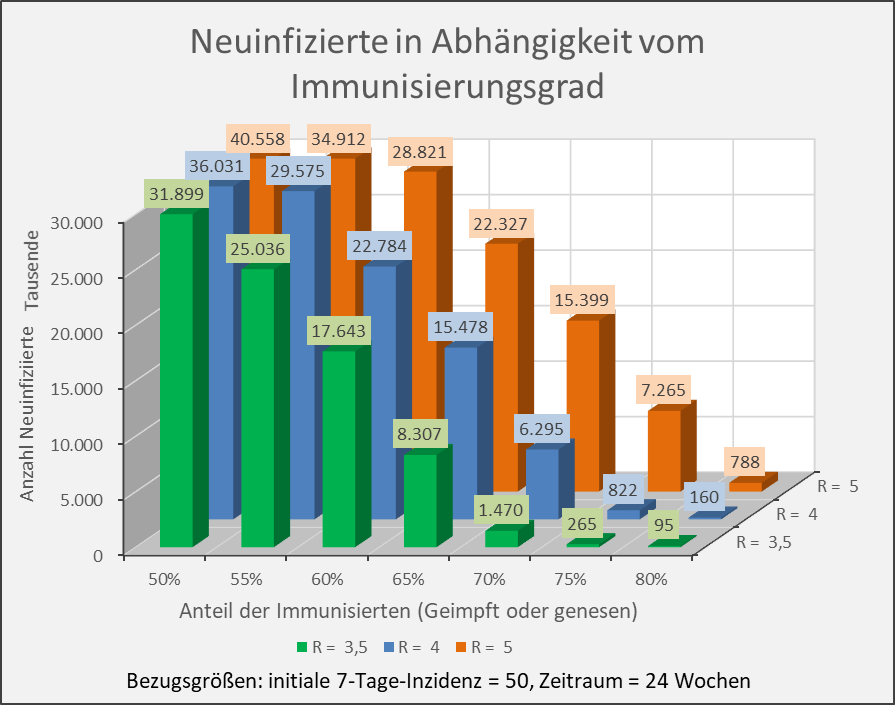
Abbildung A-5: Neuinfizierte in Abhängigkeit vom Immunisierungsgrad für R-Werte 3,5, 4 und 5. Bezugsgrößen: initiale 7-Tage-Inzidenz = 50, Zeitraum = 24 Wochen. Die Säulen zeigen jeweils die Anzahl der Neuinfektionen für die entsprechenden Wertekombinationen von Immunisierungsgrad und R-Wert. Beispiel: R-Wert = 3,5 (grüne Säulen), Immunisierungsgrad = 60 %, Neuinfizierte = 17,6 Mio. innerhalb von 24 Wochen.