Das objektive Maß für die Schwere der Pandemie ist der Einfluss auf die Lebenserwartung
Nach den sich täglich überschlagenden Horrormeldungen zu Infektionszahlen, Todesfällen und Corona-Mutanten, Impfstau, Schulschließungen, Homeoffice, Ausgangs- und Reisebeschränklungen … hat mich zunehmend die Frage interessiert, inwieweit die Corona-Pandemie die Lebenserwartung der Menschen beeinflusst. Genauer, wie stark reduzieren die beobachteten Covid-19-Todesfallzahlen die Lebenserwartung in den unterschiedlichen Altersgruppen.
Annahmen für die Berechnung der Lebenserwartung
Als Randbedingung wurde angenommen, dass die Corona-Pandemie noch ein weiteres Jahr mit der gleichen Intensität anhält und weitere etwa 50.000 Todesopfer fordert bevor 2022 die Impfungen in der Breite Wirkung zeigen werden. Sofern die Impfungen wider aller Erwartung sehr schnell erfolgen, könnte sich der Effekt auf die Reduzierung der Lebenserwartung halbieren.
Die Berechnung fußt auf den Daten des RKI (Todesfallzahlen „an oder mit“ Corona), den Sterbetafeln des Bundesamtes für Statistik (DeStatis) sowie zum Abgleich den Sterbezahlen für 2018 (Statista). Als Vergleichswerte für die Lebenserwartung wurden die Zahlen des Instituts der deutschen Wirtschaft (DeutschlandInZahlen, s. [10] und [11]) herangezogen.
Darstellung der Ergebnisse
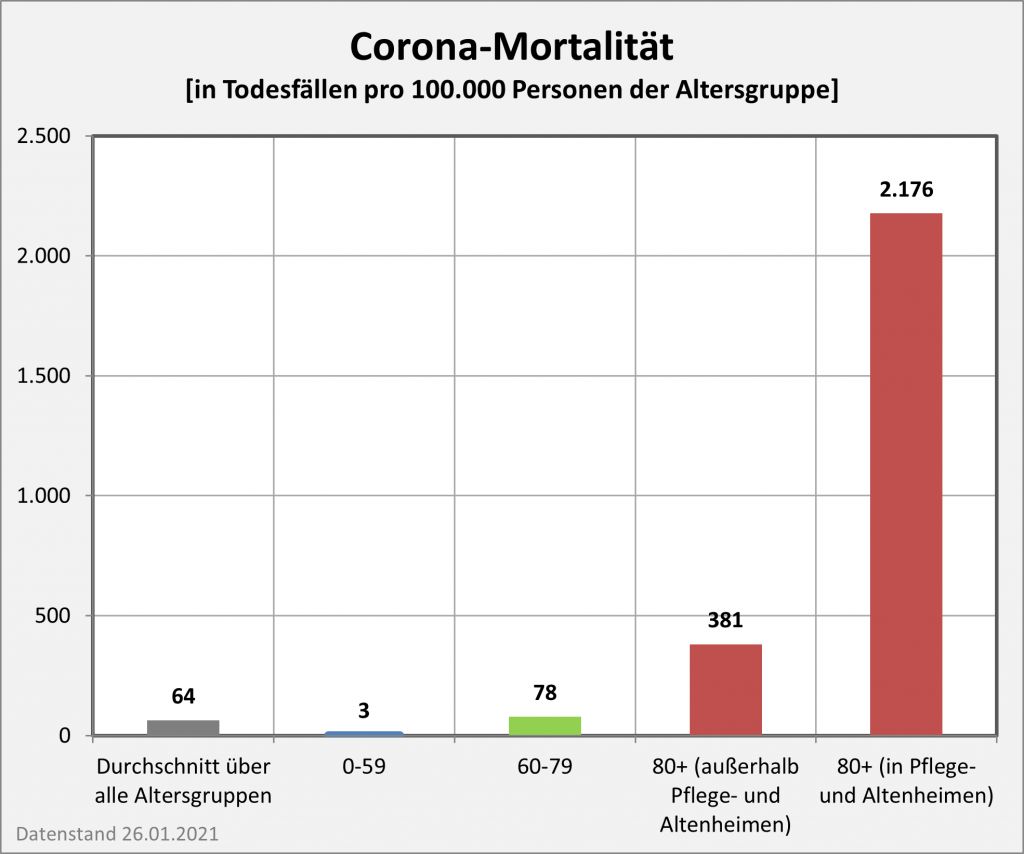
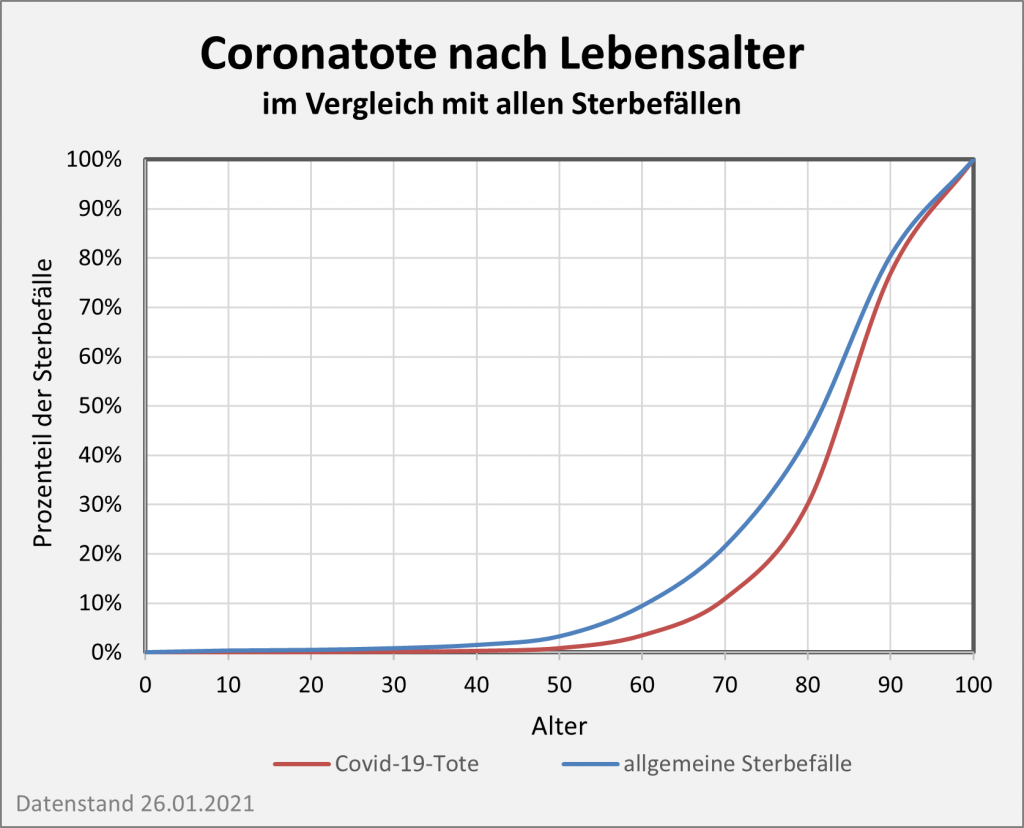
Das folgende Diagramm (s. Abb. 1) zeigt für Deutschland die Reduzierung der Lebenserwartung in der Corona-Pandemie (blaue, grüne und rote Säulen von oben nach unten). Zugrunde gelegt sind die Todesfallzahlen per 26.01.2021 in Höhe von 53.000 („an oder mit“) Covid-19-Toten in der beobachteten Altersverteilung.
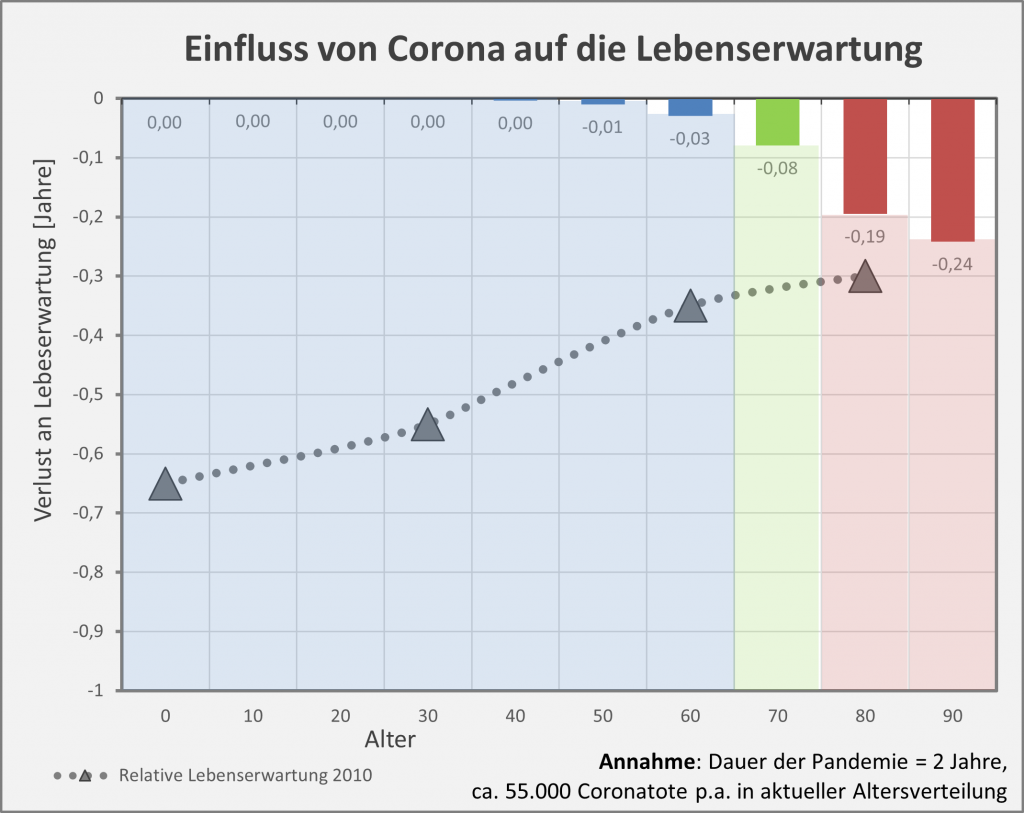
Abbildung 1: Reduzierung der Lebenserwartung in der Corona-Pandemie (blaue, grüne und rote Säulen von oben nach unten). Zugrunde gelegt sind die Todesfallzahlen per 26.01.2021 in der beobachteten Altersverteilung. Zum Vergleich: Die grau-punktierte Kurve zeigt die relative Lebenserwartung ohne Beeinträchtigung durch Corona im Jahre 2010 an.
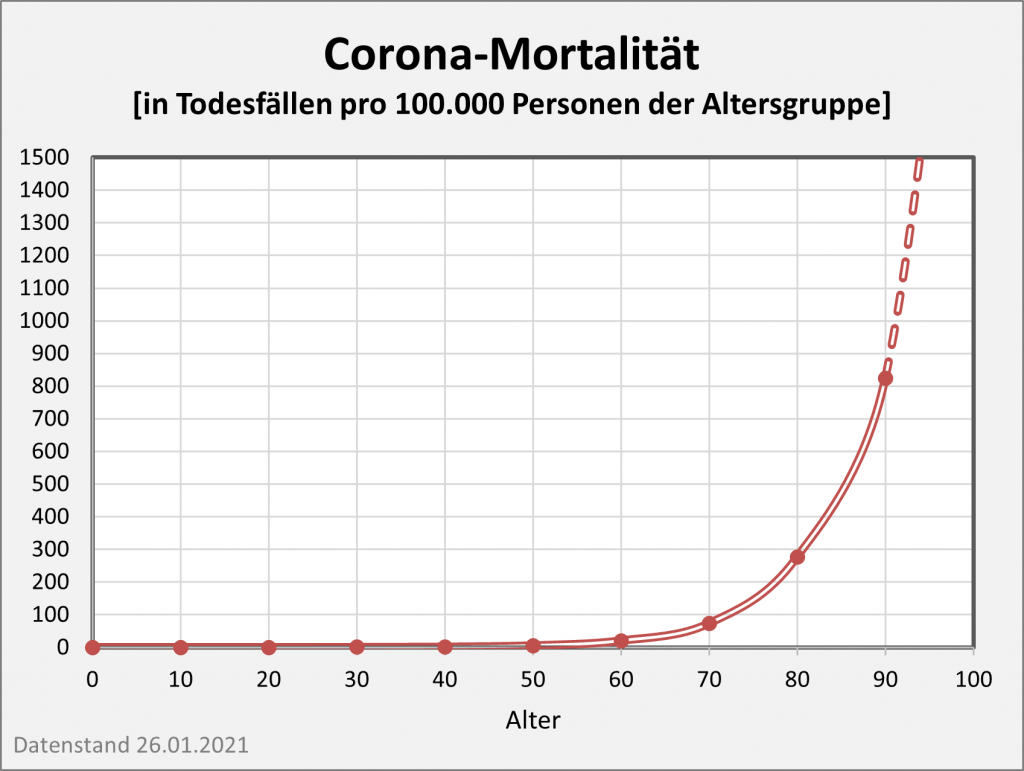
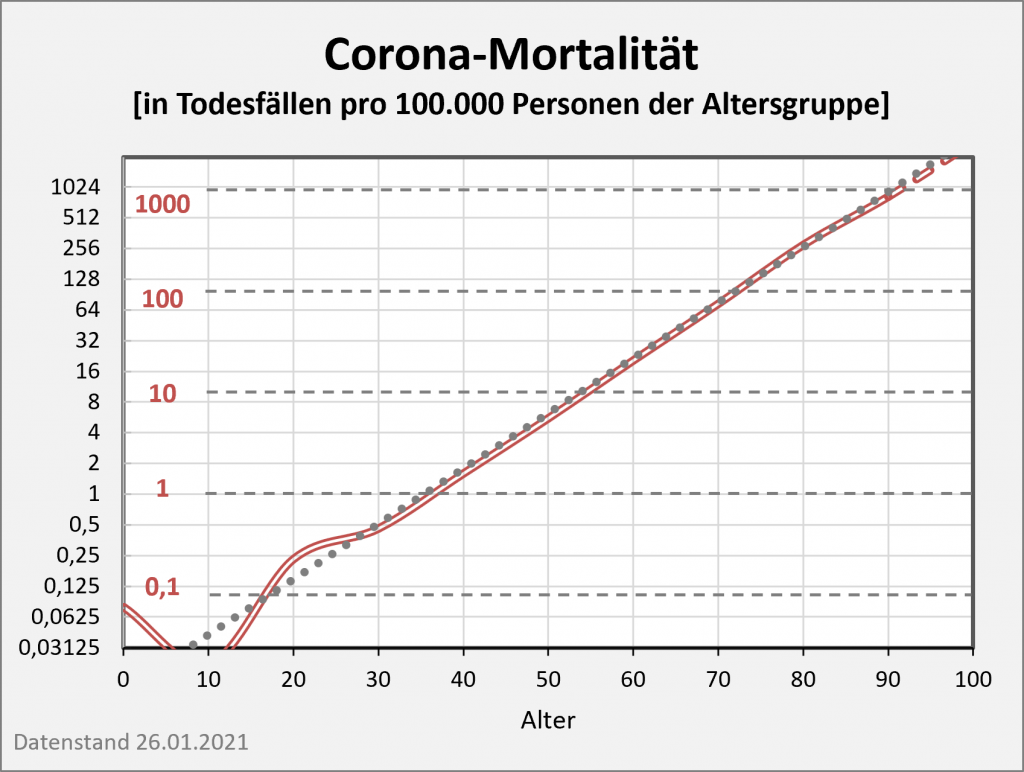
Man entnimmt der Grafik, dass für die Altersgruppen bis 50 keine messbare Reduzierung der Lebenserwartung eintritt. Für die Altersgruppen bis 70 bleibt die Reduzierung der Lebenserwartung noch unter 0,1 Lebensjahren. Für Menschen im Alter von 80 reduziert sich die Lebenserwartung um etwa 0,2 Jahre, im Alter von 90 um etwa 0,25 Jahre.
Analyse und Diskussion
Auf den ersten Blick erscheint der Einfluss überraschend gering und man fragt sich, ob dies die massiven gesellschaftlichen und wirtschaftlichen Maßnahmen und Einschränkungen der Grundrechte rechtfertigt.
Ist das vielleicht eine nicht angemessene Sicht? Sind durchschnittlich 0,2 Lebensjahre weniger doch ein größerer Einschnitt, als dies die kleine Zahl ausdrückt. Wird durch diese Betrachtung die grundsätzlich insbesondere für die Älteren bestehende Gefahr verharmlost?
Schauen wir uns zum Vergleich die allgemeine Lebenserwartung ohne Beeinträchtigung durch Corona im Jahre 2010 an (s. grau-punktierte Kurve in Abb. 1).
Die grauen Dreiecke markieren die relative Lebenserwartung im Jahre 2010 für die Lebensalter 1, 30, 60 und 80. Wie man erstaunt zur Kenntnis nimmt, war die allgemeine Lebenserwartung vor einem Jahrzehnt signifikant geringer als im Jahr 2020 unter den herrschenden Corona-Bedingungen. Konkret: Ein 80-Jähriger im Jahr 2020 hatte trotz der Corona-Gefahr immer noch eine höhere Lebenserwartung als ein 80-Jähriger im pandemiefreien Jahr 2010. Bei den Jüngeren beläuft sich der Unterschied mit 0,3 bis fast 0,7 Jahre gar auf ein Vielfaches des spezifischen Einflusses aufgrund von Corona.
Entwicklung der Lebenserwartung in den letzten 30 Jahren
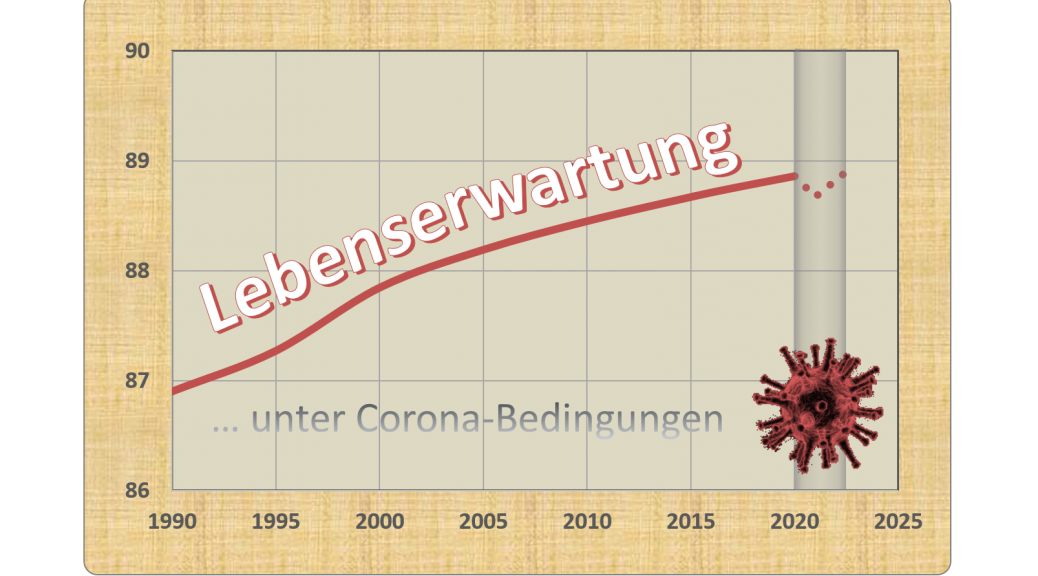
Wenn wir weiter zurückgehen, etwa auf das Jahr 1990 oder 2000, dann werden die Unterschiede noch eklatanter. In Abb. 2 ist exemplarisch die Entwicklung der Lebenserwartung seit 1990 für 30- 60- und 80-Jährige aufgetragen. Wie man den Kurvenverläufen entnimmt, war vor nur zwei Dekaden die Lebenserwartung für 80-Jährige um 0,9, für 60-Jährige gar um 1,9 Lebensjahre geringer als heute. Bei den unter 60-Jährigen (grüne und blaue Kurven) ist der Einfluss der Corona-Pandemie auf die Lebenserwartung in dieser Skalierung nicht wahrnehmbar. Aber auch der Verlauf bei den 80-Jährigen (rote Kurve) lässt nur eine kleine Delle erkennen. In Summe darf man daher festhalten: Im Vergleich zu dem in den letzten 30 Jahren registrierten Anstieg, fällt der partielle Rückgang der Lebenserwartung aufgrund von Corona nur äußerst bescheiden aus.
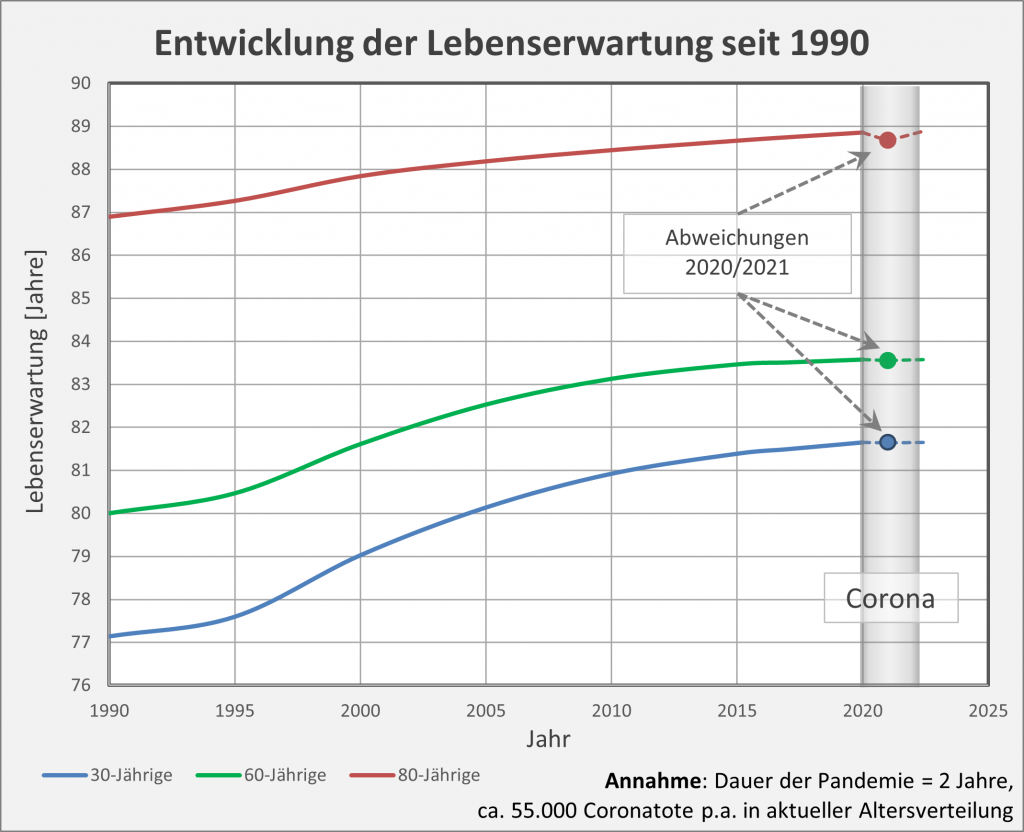
Abbildung 2: Entwicklung der Lebenserwartung seit 1990 für 30- 60- und 80-Jährige. Die Werte für die Lebenserwartung unter Corona-Bedingungen sind beim Übergang von 2020 auf 2021 jeweils durch die farbigen Punkte markiert. Mittels der grauen Säule hervorgehoben ist die Zeitspanne der Corona-Pandemie (ab Anfang 2020, im Modell verlängert bis Anfang 2022). Datenstand per 26.01.2021.
Nun sind bekanntlich insbesondere die Älteren von der Pandemie betroffen. Deswegen wollen wir den Einfluss der Corona-Pandemie für diese Gruppe schärfer herauszuarbeiten. Dazu betrachten wir den Kurvenverlauf bei den 80-Jährigen noch etwas genauer (s. hierzu Abb. 3). Wir sehen hier die gleiche Kurve wie in Abb. 2, nun aber in einem größeren Maßstab, so dass der „Einbruch“ stärker zur Geltung kommt. Der Rückgang im Vergleich zur vorherigen positiven Entwicklung der Lebenserwartung im Verlauf der letzten 30 Jahre ist unverkennbar. Man sieht aber auch deutlich, dass der Verlust an Lebenserwartung nur einen kleinen Bruchteil des Zuwachses der letzten 20 oder 30 Jahre ausmacht. In etwa beschränkt sich die Einbuße auf den in den letzten 3 – 5 Jahren verzeichneten Gewinn.
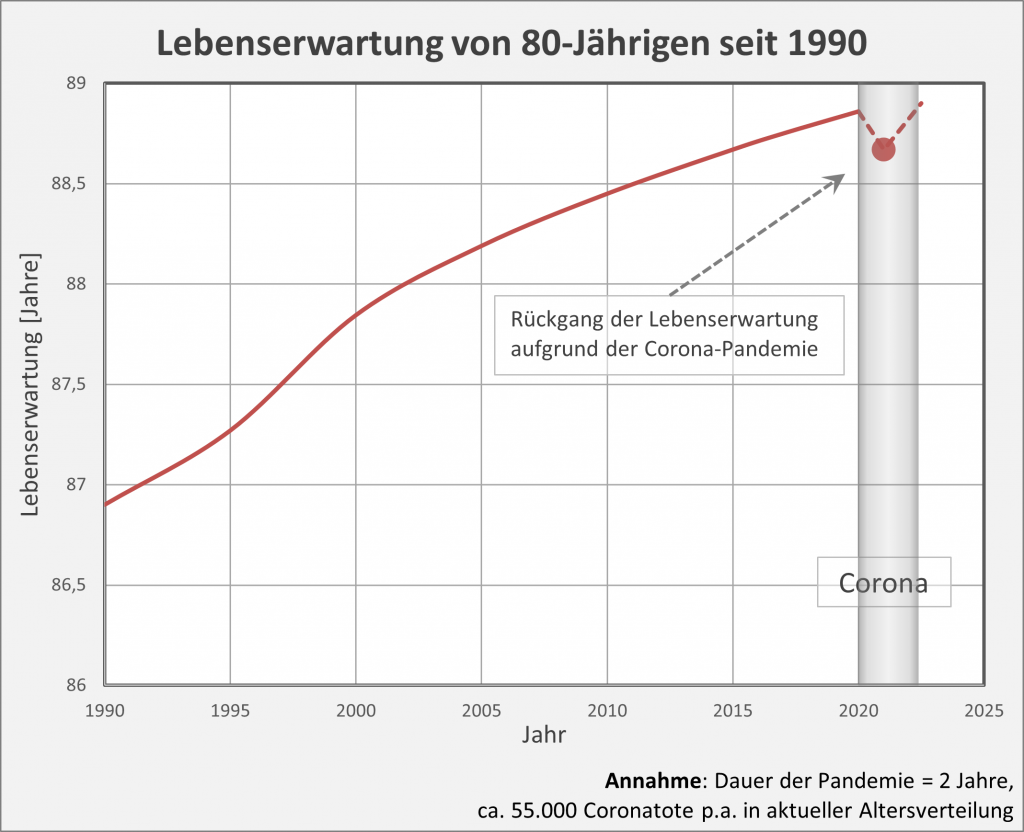
Abbildung 3: Entwicklung der Lebenserwartung für 80-Jährige von 1990 bis 2020. Der Wert für die Lebenserwartung unter Corona-Bedingungen ist beim Übergang von 2020 auf 2021 durch den roten Punkt markiert. Die graue Säule überdeckt die Zeitspanne der Corona-Pandemie (ab Anfang 2020, im Modell verlängert bis Anfang 2022). Datenstand per 26.01.2021.
Corona ein Schnippchen schlagen durch Zeitreise in die Vergangenheit?
Der zunächst verlockend klingende Gedanke, der Corona-Gefahr dadurch zu entgehen, dass man mit der Zeitmaschine zurück ins Jahr 2000 reist, würde sich nach der vorstehenden Analyse als fataler Fehler erweisen. Gegenüber der „hochriskanten“ Situation in der 2020-Corona-Pandemie würden 80-Jährige 0,7 Lebensjahre einbüßen; 60-Jährige würden gar ein noch schlechteres Geschäft machen, ihnen gingen 1,8 Lebensjahre verloren. Wohlgemerkt, wir sprechen hier vom Jahr 2000, also von der jüngsten bereits hochtechnisierten Vergangenheit, nicht von der ferneren Vorkriegszeit.
Bewertung des beobachteten Rückgangs
Auf den zweiten Blick ist daher der Einfluss der Corona-Pandemie auf die Lebenserwartung nicht nur in der absoluten Höhe, sondern auch im Vergleich mit den Vorjahren überraschend gering und man fragt sich nun erst recht, ob das die massiven Beschränkungen in allen Lebensbereichen wirklich rechtfertigt.
Damit sollen die Einzelschicksale nicht verharmlost werden. Natürlich ist jeder Tote ein Toter zu viel. Das gilt indes unabhängig von der Sterbeursache grundsätzlich auch für die 95% anderen Verstorbenen.
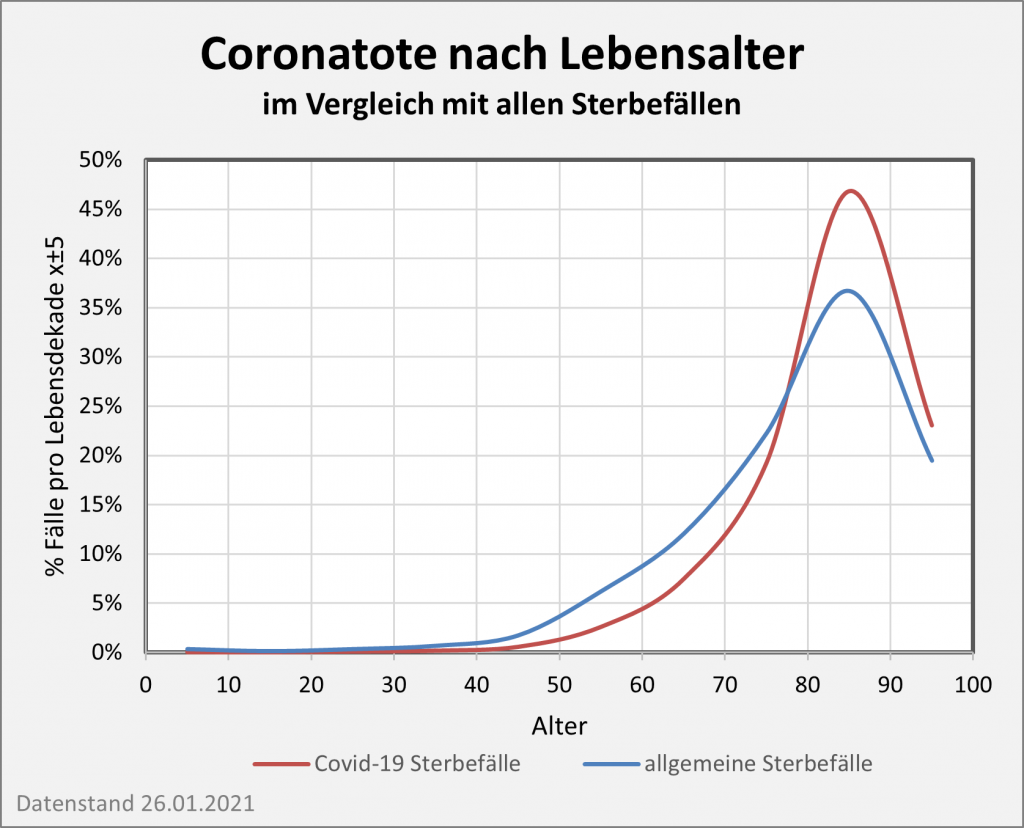
Indessen wird man mit dieser Individualbetrachtung dem Charakter einer Pandemie nicht gerecht. So hart das im Einzelfall auch klingen mag: Entscheidend für die Beurteilung der Schwere einer Pandemie sind die Auswirkungen auf die Gesamtbevölkerung. Die Individualschicksale sind nicht anders zu beurteilen als bei anderen Krankheiten auch. Täglich sterben in Deutschland etwa 2.600 Menschen, die meisten davon an Krebs und Herz-Kreislauferkrankungen. Und diesbezüglich sind die Jüngeren in Relation sehr viel stärker betroffen als von Corona.
Der oft gehörte Hinweis, das könne man nicht vergleichen, weil es sich bei Corona um ein hochansteckendes Infektionsgeschehen handelt, ist nicht stichhaltig. Natürlich kann man sich gegen diese Infektion mittels Eigenverantwortung wirksam schützen. Jedenfalls trifft dies für die sehr große Mehrheit (s. [13]) uneingeschränkt zu. Für die wenigen, die sich nicht oder nicht ausreichend schützen können, z.B. die Bewohner von Pflege- und Altenheimen, müssen aktive Schutzmaßnahmen ergriffen werden. Dazu gibt es Konzepte, die besser wirken als ein undifferenzierter Lockdown. Und insbesondere hier ist der Staat gefordert, Verantwortung zu übernehmen.
Wie schlimm würde es sein, wenn Deutschland von Trump regiert worden wäre?
Nun muss man aber auch festhalten, dass die geringe Auswirkung auf die Lebenserwartung natürlich auch eine Folge der getroffenen Schutzmaßnahmen ist. Völlig ohne Vorkehrungen wie Abstand halten, Hygiene und ggf. Maske tragen würden die Todesfallzahlen mit Sicherheit deutlich höher liegen und damit einhergehend auch der Einfluss auf die Verkürzung der Lebenserwartung markanter ausfallen.
Nehmen wir als probates Negativ-Szenario die USA, bis vor kurzem mit dem bekennenden Corona-Leugner Donald Trump an der Spitze. In den USA verzeichneten wir per Ende Januar etwa 430.000 Todesfälle. Entsprechend dem Verhältnis der Einwohnerzahl umgerechnet, wären das ca. 107.000 Todesfälle in Deutschland. Auf dieser Basis würde sich somit die Lebenserwartung für 80-Jährige um ca. 0,4 Jahre reduzieren. Für 60-Jährige und noch jüngere läge der Wert deutlich unter 0,1 Jahren und damit unter der Messbarkeitsgrenze (60-Jährige 0,06, 30-Jährige 0,023). Auch in diesem Falle haben wir eine theoretische Pandemiedauer von zwei Jahren und damit in der Projektion insgesamt 210.000 Coronatote zugrunde gelegt. Klar, die Todesfallzahlen wären etwa doppelt so hoch. Dennoch fällt es schwer, dieses Alternativszenario als unheilvolles Totalversagen zu verstehen.
Pandemie für immer
Die vorstehenden Betrachtungen wurden sämtlich unter einer markanten Randbedingung vorgenommen: Dauer der Pandemie 2 Jahre. Wie wäre es denn im Kontrast, wenn uns die Pandemie in der gegenwärtigen Schärfe mit ca. 50.000 Toten p.a. dauerhaft heimsuchen würde? Sei es, weil die Impfstoffe nicht wie erhofft wirken? Oder, weil z.B. viele neue mutierte Viren auftauchen, für die es keine effektive Behandlung gibt? Die Frage ist also, wie stark sich eine dauerhafte Corona-Pandemie auf die Lebenserwartung auswirken würde. Mit Sicherheit bliebe es nicht bei den geringfügigen Reduzierungen, wie wir sie oben gesehen haben.
Tatsächlich fällt die Verringerung der Lebenserwartung mit einer Einbuße von 0,8 Lebensjahren für 80-Jährige und etwa ein Jahr weniger Lebensspanne für 60-Jährige und Jüngere deutlich aus. Aber auch hier muss man konstatieren, dass das im schlimmsten Falle nur einen Rückschritt auf das Niveau der allgemeinen Lebenserwartung des Vergleichsjahres 2000 bedeuten würde. Keine Frage, das wäre ein drastischer Einschnitt. Mit größeren Recht als man das in der gegenwärtigen Situation ohnehin tut, würde man das als Tragödie bezeichnen. Trotz alledem wird man kaum sagen können, die Menschen zur Jahrtausendwende würden unter katastrophalen Bedingungen gelebt haben.
Die Dauer-Pandemie müssen wir nicht befürchten, umso weniger gibt es Anlass, die gegenwärtige Situation mit ihren nach obiger Analyse insgesamt noch sehr moderaten Belastungen als Katastrophe zu überhöhen.
Resümee
Das durchschnittliche Covid-19-Sterbealter liegt bei etwa 83 Jahren (s. [13]) und ist damit sogar höher als die allgemeine Lebenserwartung. Wir haben gesehen, dass die Verringerung der Lebenserwartung durch Corona für die Altersgruppen bis 70 unter 0,1 Lebensjahren bleibt. Auch für die Älteren reduziert sich die Lebenserwartung nur geringfügig: Bei einer Pandemiedauer von 2 Jahren mit 50.000 Toten p.a. büßen 80-Jährige im Durchschnitt etwa 0,2 Jahre Lebenserwartung ein, 90-Jährige etwa 0,25 Jahre.
Insgesamt ist der Einfluss der Corona-Pandemie auf die Lebenserwartung nicht nur in der absoluten Höhe, sondern auch im Vergleich mit der allgemeinen Entwicklung der Lebenserwartung in den letzten 2 bis 3 Dekaden überraschend gering. Der Verlust an Lebenserwartung macht bei den Jüngeren einen kaum messbaren, einen winzigen Bruchteil des in diesem Zeitraum verzeichneten Zuwachses aus. Sogar für die Älteren um 80 bleibt die Minderung noch unterhalb des allgemeinen Anstiegs der Lebenserwartung der letzten 10 Jahre.
Die vom Coronavirus ausgehende Gefahr für bestimmte Gruppen soll nicht verharmlost werden. Nach der vorstehenden Analyse gibt es aber auch ebenso wenig einen Grund, die Gesellschaft von einem Lockdown in den nächsten zu treiben. Stattdessen muss man diejenigen durch gezielte Maßnahmen schützen, die des Schutzes bedürfen, also insbesondere die Bewohner von Alten – und Pflegeheimen sowie die Älteren mit Vorerkrankungen. Alles andere ist völlig unverhältnismäßiger Aktionismus. Unbegründete Panikmache befeuert die allgemeine Hysterie, daraus erwächst indes kein nachhaltig wirksamer Lösungsansatz.
Quellen:
[1] Täglicher Lagebericht des RKI zur Coronavirus-Krankheit-2019 (COVID-19) – 26.01.2021 – AKTUALISIERTER STAND FÜR DEUTSCHLAND. RKI
[2] Täglicher Lagebericht des RKI zur Coronavirus-Krankheit-2019 (COVID-19) – 01.12.2020 – AKTUALISIERTER STAND FÜR DEUTSCHLAND. RKI
[3] Corona-Infektionen (COVID-19) in Deutschland nach Altersgruppe und Geschlecht (Stand: 26. Januar 2021). Statista
[4] Todesfälle mit Coronavirus (COVID-19) in Deutschland nach Alter und Geschlecht (Stand: 26. Januar 2021). Statista
[5] Bevölkerung – Zahl der Einwohner in Deutschland nach Altersgruppen am 31. Dezember 2019. Statista
[6] Altersspezifische Sterbewahrscheinlichkeiten der Männer in Deutschland. Bundesinstitut für Bevölkerungsforschung (BIB)
[7] Altersspezifische Sterbewahrscheinlichkeiten der Frauen in Deutschland. Bundesinstitut für Bevölkerungsforschung (BIB)
[8] Sterbetafel 2017/2019 – Ergebnisse aus der laufenden Berechnung von Periodensterbetafeln für Deutschland und die Bundesländer 2020. DESTATIS – Statistisches Bundesamt
[9] Anzahl der Sterbefälle in Deutschland nach Altersgruppe im Jahr 2018. Statista
[10] Tabelle: Lebenserwartung (Männer) – in Jahren
[11] Tabelle: Lebenserwartung (Frauen) – in Jahren
[12] Das „Vorsorgeprinzip“ der Kanzlerin in der Pandemie ist einseitig
[13] Die Corona-Pandemie: Alter ist der dominierende Risikofaktor
https://www.linkedin.com/pulse/die-corona-pandemie-alter-ist-der-hauptrisikofaktor-fischer/
[14] Das Coronavirus: Harmlos? Bedrohlich? Tödlich?
https://www.linkedin.com/pulse/das-coronavirus-harmlos-bedrohlich-t%C3%B6dlich-hieronymus-fischer
[15] Aktuelles zu Corona