Eine kritische Bilanz
Das Jahr 2021 ist vorbei und die Corona-Zahlen liegen nun vor. Zu Beginn des Jahres 2021 konnte man erwarten, dass sich das schlimme Corona-Jahr 2020 nicht wiederholen würde, schließlich standen mehrere Impfstoffe zur Verfügung. Allenfalls konnte man es für eine Frage der Organisation halten, bis hinreichend viele Menschen geimpft und die Pandemie damit mehr oder weniger zu Ende sei.
Heute sind wir alle klüger: Die Zahlen für 2021 sind dramatischer als die für 2020 – trotz der Impfung. Fast dreimal so viele Infizierte und immerhin 59% mehr Tote. Mittlerweile wissen wir auch, dass zweimal Impfen nicht reicht. Absehbar ist auch nach der dritten Spritze keine wirkliche Immunität gegeben. Die Impfung schützt zwar oft vor schweren Krankheitsverläufen und Tod, aber wenig vor einer Infektion und vor dem Weitertragen des Virus. Auch Geimpfte sind also nach wie vor Teil der Infektionsdynamik. Zudem ist bekannt, dass der Schutz der Impfung bereits binnen 3 – 4 Monaten nachlässt und der Impfstoff nach 6 Monaten und mehr, je nach Alter, nur noch eine schwache Wirkung entfaltet. Die daraus folgende Problematik wird im Text diskutiert und anhand vieler Grafiken visualisiert.
Konkret werden im Artikel die Zahlen zu den Infektionen und den Todesfällen für 2020 und 2021 insgesamt und getrennt nach Altersgruppen nebeneinander gestellt und miteinander verglichen. Ferner werden die Infektionsrisiken, die Letalitätswerte (Sterblichkeit nach Corona-Infektion) und die Mortalität (Corona-Sterblichkeit in der Bevölkerung) altersgruppenspezifisch bestimmt und zueinander in Relation gesetzt.
Aus der tiefergehenden Untersuchung zu den Zahlen für 2021 werden Schlüsse zum altersabhängigen Risiko gezogen: Letalität und Mortalität steigen exponentiell mit dem Lebensalter. Die Sterblichkeit nach einer Infektion (Letalität) verzehnfacht sich pro 18 Lebensjahren. Die Mortalität verzehnfacht sich pro 22 Lebensjahren. Um das richtig einzuordnen, muss man erwähnen, dass das absolute Corona-Sterberisiko von 18-Jährigen bei etwa 0,0005% liegt, das von 84-Jährigen bei etwa 0,5%.
Auf Basis von Überlegungen zur Ableitung der unterschiedlichen Sterberisiken für Geimpfte und Ungeimpfte aus den verfügbaren Felddaten, erfolgt im letzten Teil eine Was-Wäre-Wenn-Analyse. Basierend auf den realen Daten aus 2021 werden dabei hypothetische Szenarien mit und ohne Impfung durchgerechnet und miteinander verglichen. Der Schluss gehört der Betrachtung von diversen Alternativszenarien mit unterschiedlichen altersgruppenspezifischen Impfquoten. Dafür werden die unter den getroffenen Annahmen wahrscheinlichen Fallzahlen bestimmt, auch im Hinblick auf Geimpfte und Ungeimpfte.
Infizierte und Todesfälle – Vergleich 2020/2021
Die nachfolgend präsentierten Corona-Grafiken und Analysen basieren sämtlich auf dem vom Robert-Koch-Institut (RKI) veröffentlichten Zahlenmaterial. Die entsprechenden Referenzen sind im Quellenverzeichnis aufgeführt.
Die Corona-Impfquoten, die Inzidenzen bezüglich der Infizierten, der Hospitalisierten und der Corona-Todesfälle werden vom RKI in hoher zeitlicher Auflösung publiziert. Man muss die Erfassungssystematik nicht in jedem Detail für gelungen und zweckmäßig halten, in Summe ist das RKI dennoch die einzige einigermaßen verlässliche Corona-Datenquelle. Es gibt kleinere Unschärfen, z.B. bezüglich der Impfquoten, und es gibt eklatante Mängel, z.B. hinsichtlich des Erfassung des Impfstatus der Infizierten, der Hospitalisierten und der Todesfälle. Immerhin werden seit August 2021 für die symptomatischen Fälle die Infektionszahlen getrennt nach Geimpften und Ungeimpften erfasst. Weitere für die Analyse wichtige Einflussgrößen wie die verstrichene Zeitspanne seit der Impfung oder das effektive Ansteckungsrisiko aufgrund des Kontaktprofils werden nicht dokumentiert und können daher auch nicht ausgewertet werden.
Die Inzidenzen der Corona-Infektionen und der Fälle der „an oder mit“ Corona Verstorbenen nehmen wir einfach so, wie sie vom RKI veröffentlich wurden, auch wenn man bezüglich der Höhe der Zahlen berechtigte Zweifel ins Feld führen kann. Tatsächlich könnten die Infektionszahlen deutlich höher gelegen haben, weil viele Infektionen unerkannt geblieben sind. Die Zusammensetzung der Testkohorte spiegelt lediglich rechtliche Vorgaben wider. Nötig wäre aber eine Orientierung an wissenschaftlichen Grundsätzen. In letzter Konsequenz sind daher die veröffentlichten Inzidenzen nur grobe Schätzungen.
Umgekehrt könnten viele Todesfälle fälschlicherweise Corona zugerechnet worden sein, weil die Todeskausalität in vielen Fällen nicht näher untersucht worden ist. In letzter Konsequenz könnte die Infektiosität in Wahrheit höher und die Letalität (Sterblichkeit bei einer Corona-Infektion) tatsächlich kleiner sein, als sich dies aus den Zahlen des RKI ergibt. Das ist hier indessen nicht das Thema: Wir stützen uns auf die Daten des RKI, nichts sonst. Alles andere wäre Spekulation.
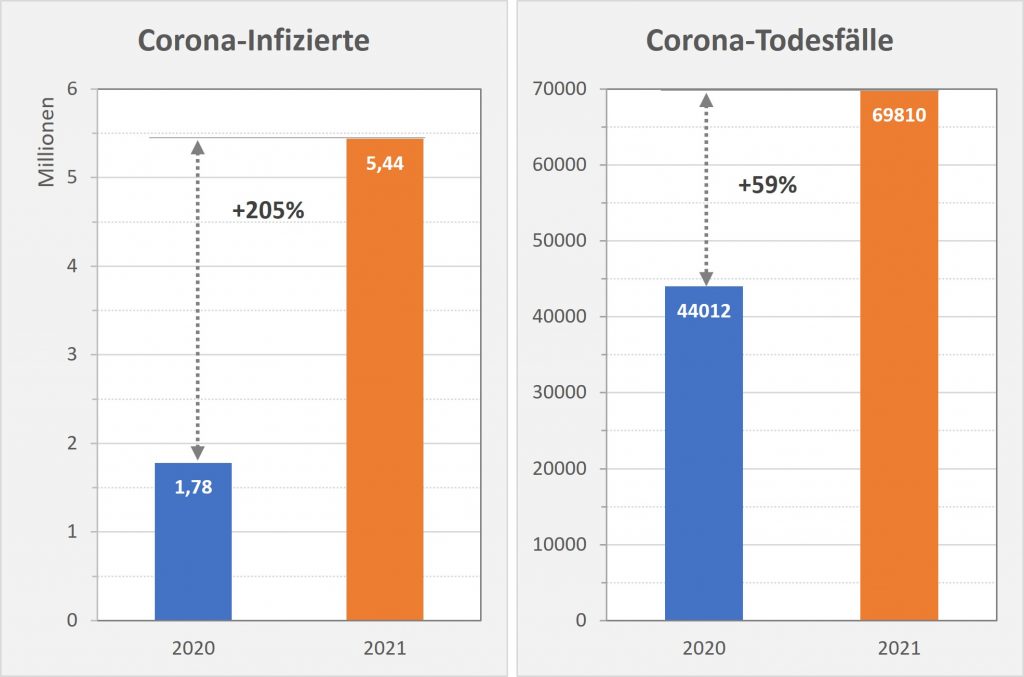
Abbildung 1: Corona-Infizierte und -Todesfälle 2020 und 2021 im direkten Vergleich. Man erkennt, dass sich die Infektionszahlen in 2021 gegenüber 2020 in etwa verdreifacht haben. Die Anzahl der Todesfälle ist um ca. 59 % gestiegen. Rohdaten: RKI, Datenstand 22.01.2022.
In Abb. 1 fällt zunächst die hohe Zahl der Infizierten in 2021 auf. Gegenüber 2020 (mit 10 Monaten Pandemiedauer) haben wir in 2021 ein volles Jahr. Das kann den Anstieg sicher nicht erklären. Offenbar liegt ein Grund eher in der höheren Infektiosität der Deltavariante des Virus. Die Anfang 2021 angelaufene Impfkampagne hatte auf die Anzahl der Infektionen offenbar keinen dämpfenden Einfluss. Mit Blick die Todesfallzahlen registriert man den vergleichsweisen deutlich geringeren Anstieg. Ist das womöglich ein Erfolg der Impfung? – Teilweise sicher ja, der Effekt ist aber wohl geringer, als dies der erste Anschein vermuten lässt. Näheres dazu mit einer genauen Analyse weiter unten.
Infizierte und Todesfälle nach Altersgruppen – Vergleich 2020/2021
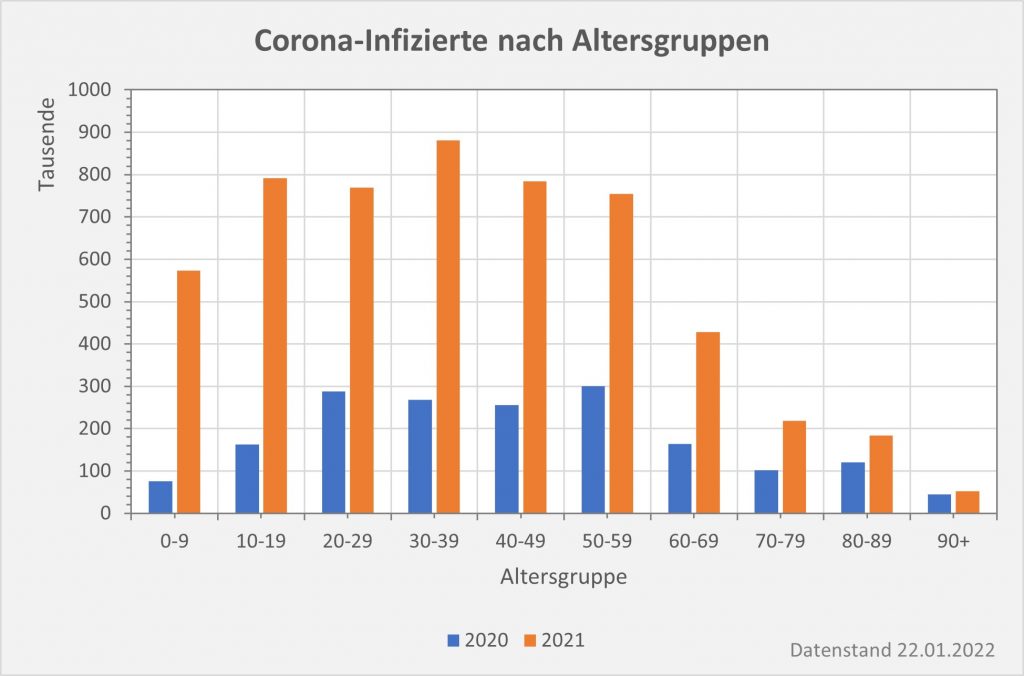
Abbildung 2: Corona-Infizierte 2020 und 2021 nach Altersgruppen im direkten Vergleich. Wie man sieht, sind in 2021 insbesondere die Infektionszahlen bei den jüngeren Altersgruppen erheblich gestiegen. Rohdaten: RKI, Datenstand 22.01.2022.

Abbildung 3: Corona-Todesfälle 2020 und 2021 nach Altersgruppen im direkten Vergleich. Die absoluten Fallzahlen zeigen einen Anstieg insbesondere bei den Über-50-Jährigen. Das größere relative Wachstum verzeichnet man bei den Jüngeren. In der Gesamtschau sind aber dennoch die Älteren mit großem Abstand dominierend. Allein der Zuwachs in 2021 ist bei den Älteren (60+) viermal höher als die Gesamtanzahl der Toten bei den Jüngeren (0-59). Rohdaten: RKI, Datenstand 22.01.2022.
Beim Vergleich der beiden Grafiken nach Abb. 2 und 3 fällt auf, dass die Infektionszahlen weit überwiegend von den Altersgruppen unter 60 getrieben werden, die Todesfälle passieren aber nach wie vor zum größten Teil in der Altersgruppe ab 60. Das werden wir weiter unten genauer beleuchten.
Am vorstehenden Befund hat sich auch durch die Verfügbarkeit von Impfstoffen und der seit Januar 2021 laufenden Impfkampagne offenbar nichts oder nur wenig geändert. Jedenfalls ist der Effekt hier nicht sichtbar. Dabei waren doch gerade die Über-80-Jährigen schon früh im Jahr mit hoher Priorität und in großer Zahl geimpft worden.
Die folgende Abbildung mit zusammengefassten Altersgruppen untermauert dieses vorläufige Resümee in aller Deutlichkeit.
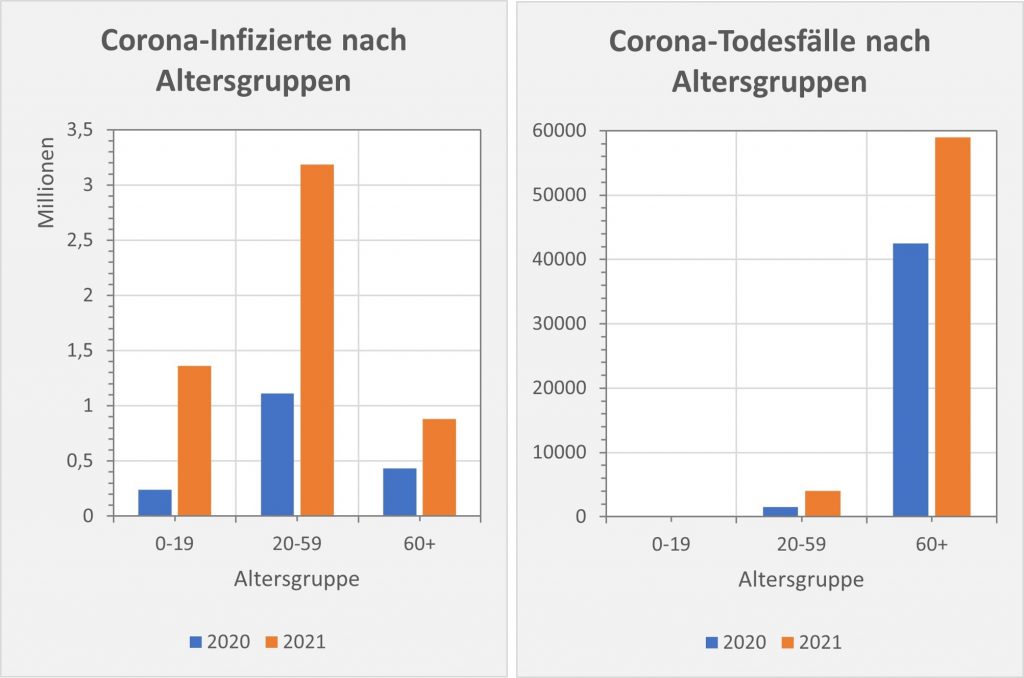
Abbildung 4: Corona-Infizierte und -Todesfälle 2020 und 2021 in ausgewählten Altersgruppen im direkten Vergleich. Bei der Betrachtung der aggregierten Altersgruppen sieht man nochmals deutlicher den starken Anstieg der Infektionen bei den Jüngeren. Tatsächlich ist die Anzahl der Infektionen in der Altersgruppe 0-59 gegenüber 2020 um über 200 % gewachsen. In der Altersgruppe 60+ haben sie sich dagegen nur um gut 100% erhöht. Zugleich sind hier auch die Todesfallzahlen weit weniger gestiegen. Rohdaten: RKI, Datenstand 22.01.2022.
Wenn man den Zahlen etwas Positives abgewinnen will, dann kann man an dieser Stelle immerhin darauf hinweisen, dass die Todesfallzahlen (+53 %) in der Altersgruppe 60+ weniger gewachsen sind als die Infektionszahlen (+104 %). Das darf man zum Teil sicher auch der Impfung zurechnen. Wie groß der Effekt tatsächlich ist, werden wir weiter unten genauer untersuchen. In der Altersgruppe 20-59 (mit einer im Jahresmittel geringen Impfquote) sind die Todesfallzahlen (+202 %) hingegen fast genau so schnell gestiegen wie die Infektionszahlen (+237 %).
Infizierte und Todesfälle nach Altersgruppen – Analyse für 2021
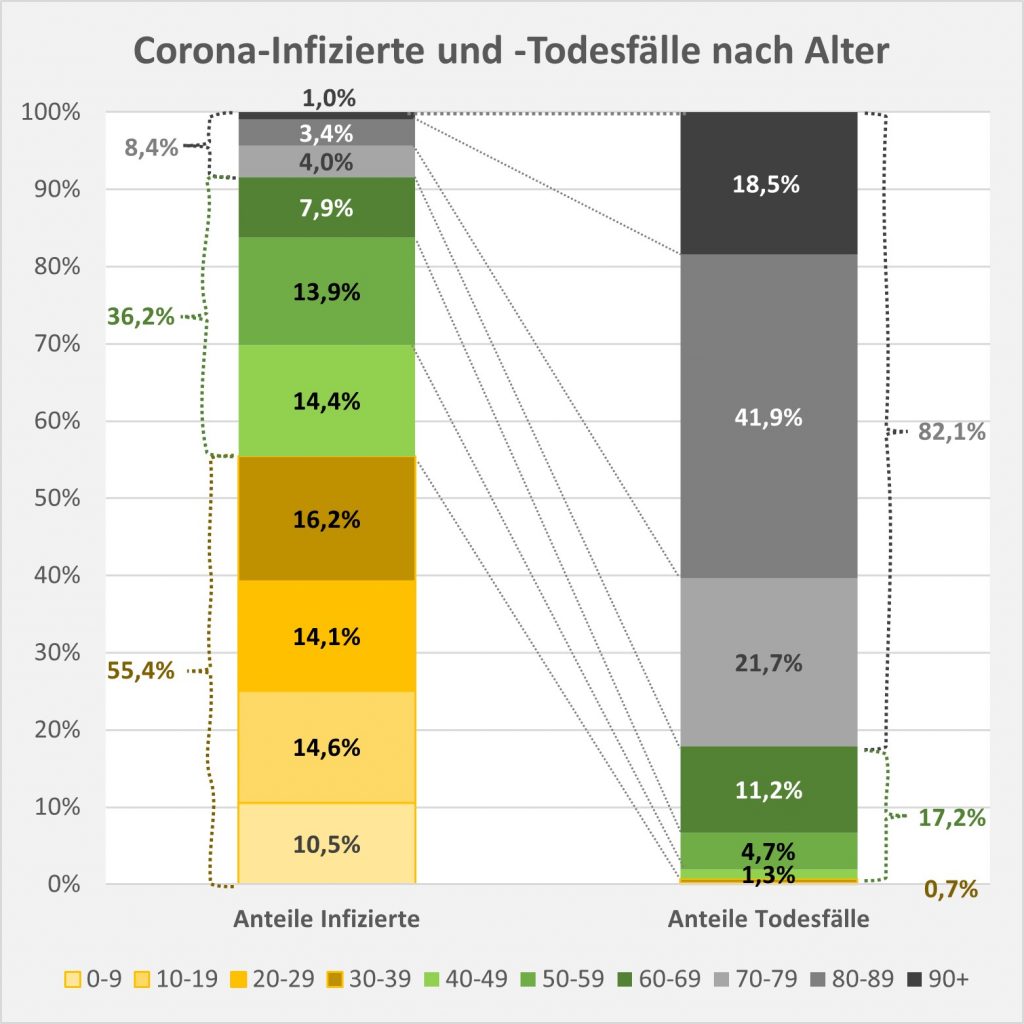
Abbildung 5: Relative Anteile der Corona-Infizierten und -Todesfälle 2021 nach Altersgruppen. In der linken Säule sind die Infizierten nach ihrem jeweiligen Anteil farbcodiert eingetragen. Die rechte Säule weist entsprechend die altersgruppenspezifischen Anteile unter den Todesfallzahlen aus. Man erkennt, dass die Infektionen überwiegend bei den Jüngeren auftreten, die Todesfälle indes bei den Älteren. Die gelb-braunen Farbtöne in der linken Säule stehen für die Altersgruppe 0-39 mit einem Anteil an den Infektionen von über 55%. In der rechten Säule kann man diese Farbtöne kaum ausmachen. Der Anteil an den Todesfallzahlen liegt bei etwa 0,7%. Umgekehrt am oberen Ende der Säule: 8,4% der Infizierten werden der Altersgruppe 70+ zugerechnet. Zugleich stellt diese Gruppe 82% aller Corona-Toten. Rohdaten: RKI, Datenstand 22.01.2022.
Auch wenn man mit Blick auf Abb. 5 dem ersten Anschein nach denkt, es sei anders: Die Farbcodierung ist in beiden Säulen gleich. Die ausgeprägt asymmetrische Verteilung zwischen Infektionszahlen und Todesfällen über die Altersgruppen hinweg wird mittels der Grafik klar vor Augen geführt. Das wirft ein denkbar grelles Licht auf die Corona-Maßnahmen. Abgesehen von der prioritären Impfung der Ältesten setzen sie überwiegend an der linken Säule im gelb-braunen und im grünen Bereich an (Altersgruppen 0-39 und 50-69). Der Effekt soll sich aber in der rechten Säule zeigen, wo diese Gruppen gerade einmal 17% ausmachen.
Das ist in etwa so, als würde man nach der Brandmeldung im Seniorenstift die Feuerwehr zur Grundschule schicken.
Es zeigt sich hier überdeutlich, dass viele der getroffenen Maßnahmen schon deswegen nicht wirken können, weil sie am falschen Ende ansetzen. Vielleich noch etwas klarer kommt das mittels der nachfolgenden beiden Abbildungen zum Ausdruck.
In der ersten (Abb. 6) sind die Altersgruppen teilweise zusammengefasst, um die zentrale Botschaft noch stärker hervortreten zu lassen. In der zweiten (Abb. 7) wurde eine andere Darstellung gewählt.
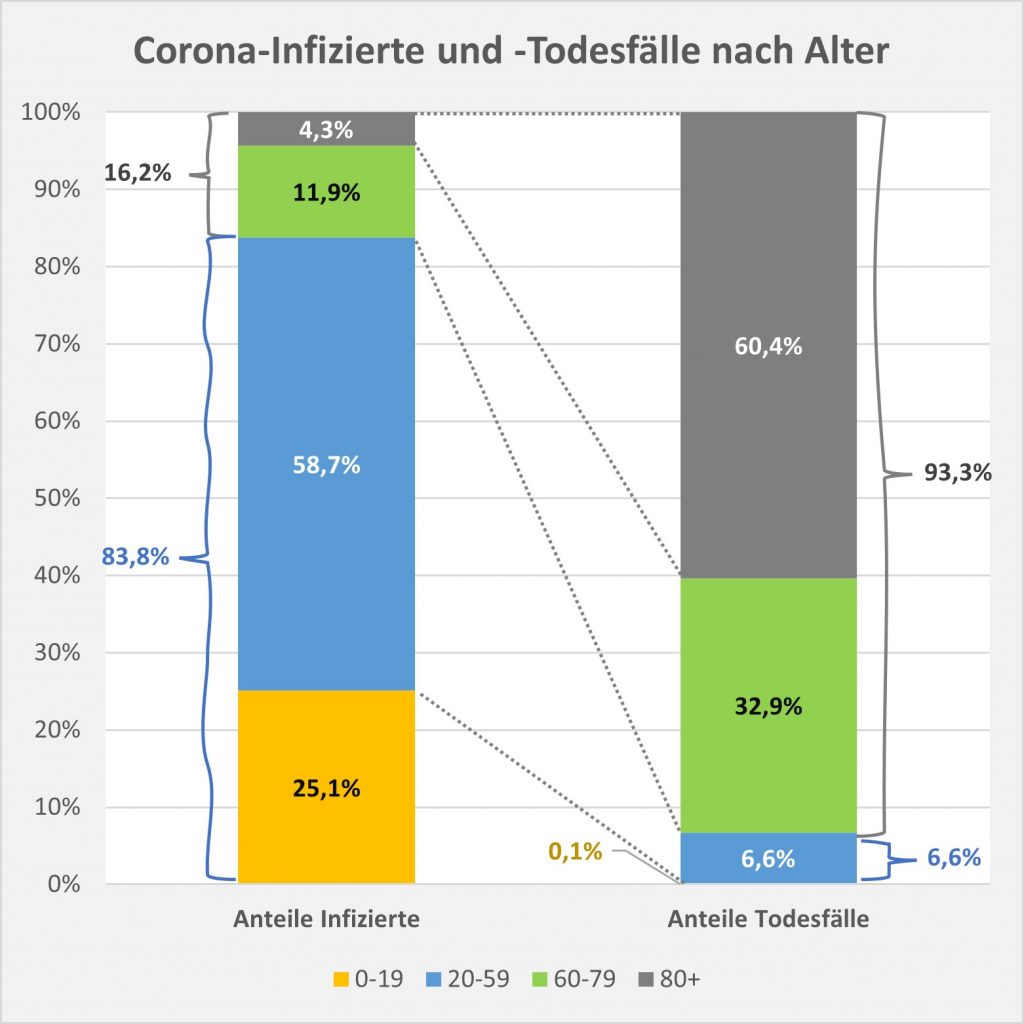
Abbildung 6: Relative Anteile der Corona-Infizierten und -Todesfälle 2021 nach ausgewählten Altersgruppen. In der linken Säule sind die Infizierten nach ihrem jeweiligen Anteil farbcodiert eingetragen. Die rechte Säule weist entsprechend die altersgruppenspezifischen Anteile unter den Todesfallzahlen aus. Man erkennt, dass die Infektionen überwiegend bei den Jüngeren auftreten, die Todesfälle indes bei den Älteren. Die Altersgruppe 0-19 stellt 25% der Infizierten, aber nur 0,1% der Todesfälle. Dem fast 84%-igen Anteil der den Altersgruppen 0-19 und 20-59 zugerechneten Infektionen stehen 6,6% der Todesfälle entgegen. Dagegen treten 93,3% der Todesfälle in den Altersgruppen 60-79 und 80+ auf, die ihrerseits nur etwa 16% der Infektionsfälle zu verantworten haben. Rohdaten: RKI, Datenstand 22.01.2022.
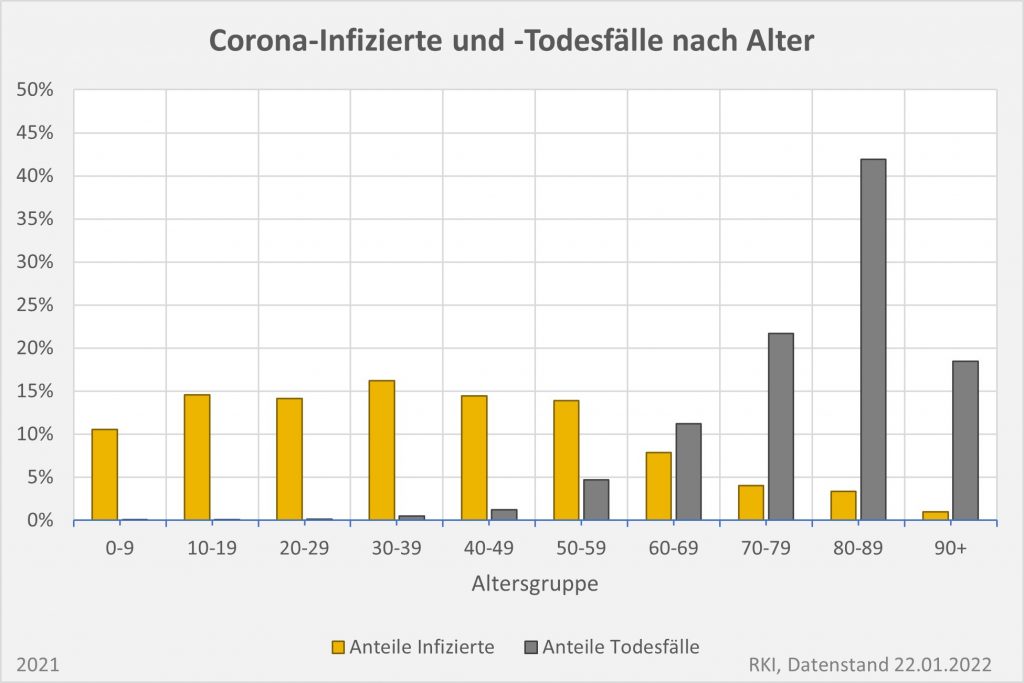
Abbildung 7: Relative Anteile der Corona-Infizierten und -Todesfälle 2021 nach Altersgruppen. Die gelben Säulen zeigen die relativen Infektionshäufigkeiten, die grauen die Todesfälle. Kurz gefasst sieht man auch hier, dass die Infektionen und die Todesfälle in unterschiedlichen Altersgruppen auftreten. Wo nur noch ein Bruchteil der Infektionen verzeichnet wird, sind die Todesfallzahlen am höchsten. Rohdaten: RKI, Datenstand 22.01.2022.
Die Unwirksamkeit vieler politisch verfügter Corona-Maßnahmen kann nach dieser Betrachtung kaum noch verwundern: Sie gehen schlichtweg am Ziel vorbei.
Um den obigen Feuerwehrvergleich nochmals aufzunehmen: Natürlich ist die potentielle Brandgefahr bei der Grundschule endgültig gebannt, die Feuerwehr ist ja schon vor Ort. Das kann sich man als Erfolg schönreden. Aber: Der Unterricht ist gestört und die Schüler leiden. Zugleich steht das Seniorenstift lichterloh in Flammen.
Überblick zu den kritischen Größen Infektionsrisiko, Letalität und Mortalität
Grundsätzlich gilt zwischen den drei Faktoren Infektionsrisiko, Letalität und Mortalität der folgende Zusammenhang:
Mortalität = Infektionsrisiko * Letalität
Die Begriffe selbst werden in [9] Das Coronavirus: Harmlos? Bedrohlich? Tödlich? – sumymus blog näher erläutert. Hier eine kurze Zusammenfassung:
Die Mortalität ist der relative Anteil der an einer bestimmten Krankheit Verstorbenen bezogen auf die Gesamtheit der Bevölkerung oder bezogen auf eine bestimmte Personengruppe (z.B. Menschen eines gegebenen Alters oder die Bevölkerung in einer Region).
Die Letalität ist der relative Anteil der Verstorbenen bezogen auf die Gesamtheit der Infizierten oder die Gesamtheit der Infizierten einer bestimmten Personengruppe.
Das Infektionsrisiko beschreibt die Wahrscheinlichkeit für eine (Coronavirus-)Infektion. Es ist abhängig von den Eigenschaften des Virus, von den Umweltbedingungen, von individuellen Faktoren sowie von Maßnahmen zur Kontrolle der Verbreitung des Virus.
Die Letalität ist ein Maß für die Gefährlichkeit des Virus bzw. der Infektion bei gegebener Leistungsfähigkeit des Gesundheitssystems und gegebenem Gesundheitszustand des betreffenden Personenkreises sowie ggf. auch der Impfung. Dagegen misst die Mortalität darüber hinaus das Infektions- bzw. Erkrankungsrisiko. In Bezug auf Corona steckt in der Maßzahl der Mortalität somit auch die Wirksamkeit von Schutzmaßnahmen.
Bei 100%-iger Wirksamkeit der Schutzmaßnahmen ist das Infektionsrisiko = 0 und somit die spezifische Mortalität ebenfalls 0. Ohne Schutzmaßnahmen oder mit wenig effektiven Schutzmaßnahmen liegt das Infektionsrisiko in Abhängigkeit von individuellen Faktoren (z.B. Kontakthäufigkeit, Kontaktdauer, Kontaktintensität) irgendwo zwischen 0 und 100%. Im Extremfall, wenn alle Personen der relevanten Bezugsgruppe infiziert sind, ist die Mortalität gleich der Letalität.
Letalität nach Altersgruppen – Vergleich 2020/2021
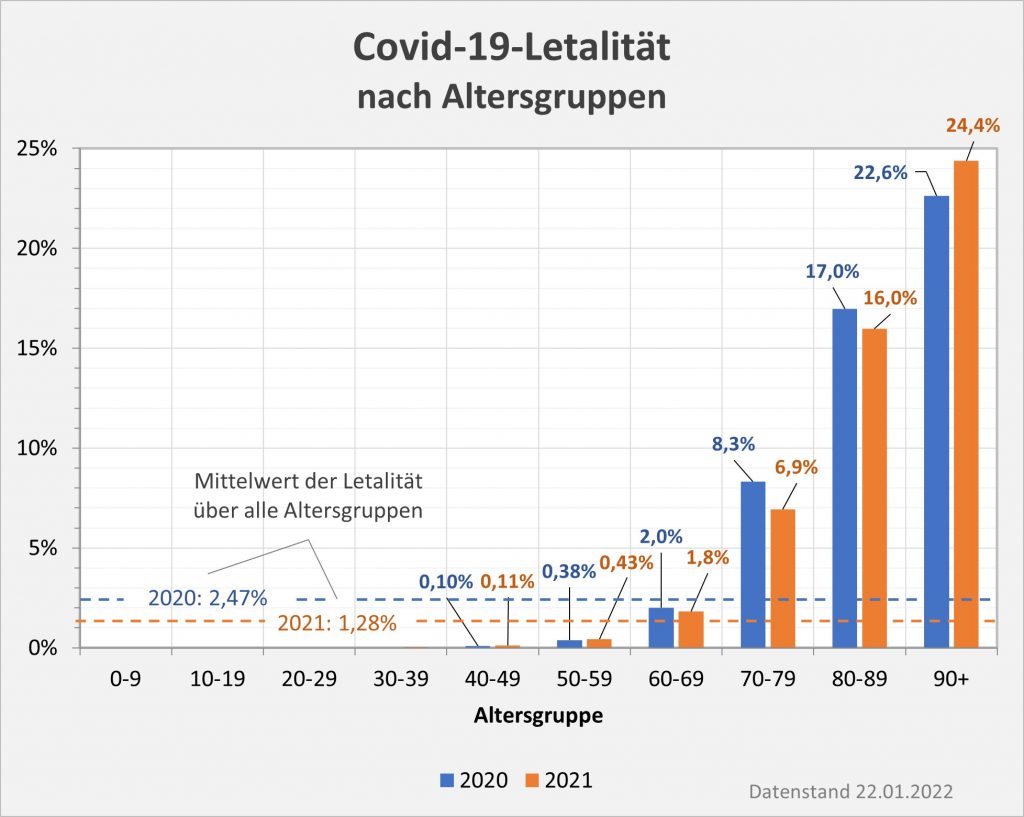
Abbildung 8: Covid-19-Letalität (Sterblichkeitsrate nach einer Corona-Infektion) für 2020 und 2021 nach Altersgruppen im Vergleich. Für 2021 ist jeweils der Letalitätswert explizit eingetragen. Man sieht, dass die 2021er-Säulen meist etwas kürzer sind als die 2020er. Stark gesunken ist die mittlere Sterblichkeit über alle Altersgruppen. Sie hat sich von 2,47% in 2020 auf 1,28% in 2021 etwa halbiert. Dieser positive Effekt ist indes nur zu einem geringen Teil auf die Impfung zurückzuführen. Trotz der sehr hohen Impfquote in der Altersgruppe 90+ ist die Letalität für die Ältesten sogar gestiegen. Rohdaten: RKI, Datenstand 22.01.2022.
Wie man Abb. 8 entnimmt, ist die Sterblichkeit nach einer Corona-Infektion in einigen Altersgruppen zurückgegangen, in anderen gestiegen, wenn auch beides nur geringfügig. Für die Altersgruppen ab 60 liegt die Letalität in 2021 aber immer noch höher als 1%, zum Teil drastisch höher. Die anderen Altersgruppen, also alle unter 60, weisen hingegen viel kleinere Sterblichkeitsraten p.a. auf. Unter-40-Jährige liegen bei max. 0,03%. Im Diagramm sind diese Säulen skalierungsbedingt daher nicht mehr sichtbar.
Der Rückgang der durchschnittlichen Sterblichkeit (nach einer Corona-Infektion) über alle Altersgruppen in 2021 ist i. W. auf die hohen Infektionszahlen bei den Jüngeren, wie sie oben dokumentiert wurden, zurückzuführen. Sie sind wenig von schweren Verläufen und Tod betroffen und tragen daher kaum zu den Todesfällen bei. Es ist also ein statistischer Effekt.
Um das an einem Beispiel plausibel zu machen: Wenn sich die Infektionszahlen in der Altersgruppe 0-39 verdoppeln, dann hat dies auf die Todesfallzahlen keinen nennenswerten Einfluss. Allenfalls werden die Beträge in Summe um einige 100 Fälle steigen. Prozentual würde das weniger als ein Prozent ausmachen. Zugleich würden aber die Infektionszahlen insgesamt um mehr als 50% steigen. Im Ergebnis würde daher die Sterblichkeitsrate p.a. nach Corona-Infektion auf etwa Zweidrittel (1/1,5) des aktuellen Wertes sinken (also -33%). Und dies völlig ohne irgendeine steuernde Maßnahme, wie z.B. eine Impfpflicht. Genau diesen Effekt kann man in 2021 im Vergleich zu 2020 beobachten, wie wir oben gesehen haben (s. Abb. 3 und 4).
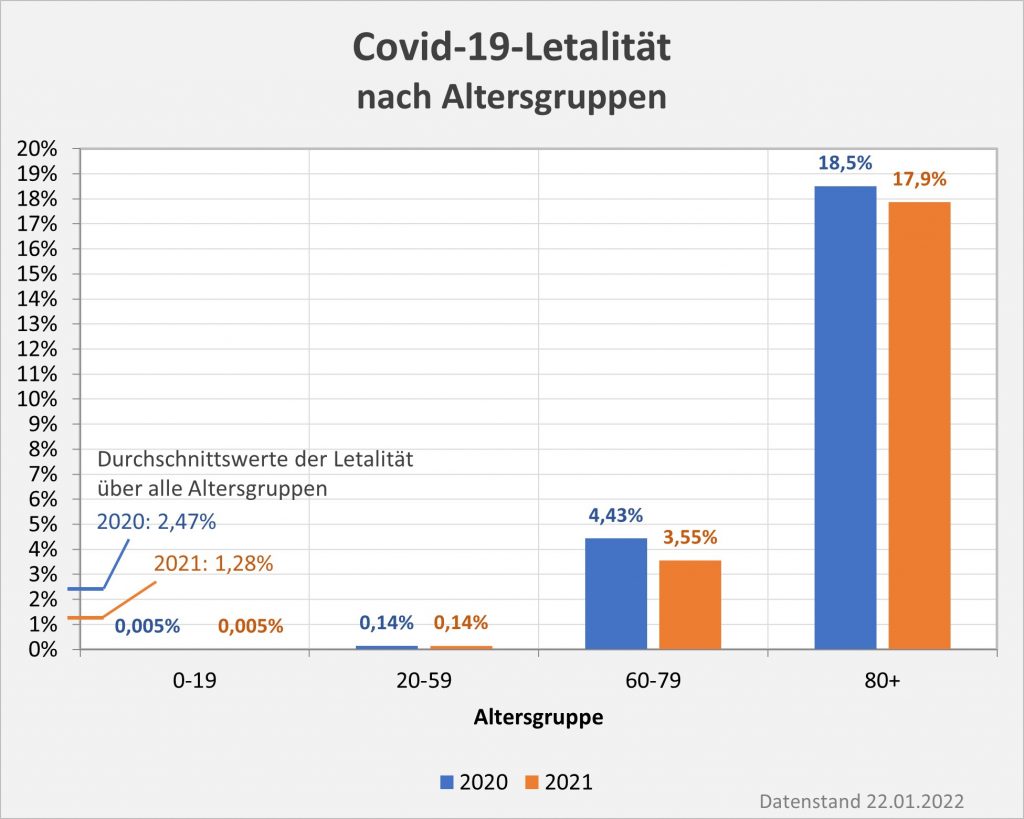
Abbildung 9: Covid-19-Letalität (Sterblichkeit nach einer Corona-Infektion) für 2020 und 2021 in ausgewählten Altersgruppen im Vergleich. In der Relation erkennt man in den höheren Altersgruppen den Rückgang der Sterblichkeit nach einer Infektion. Die mittlere Sterblichkeit über alle Altersgruppen hat sich von 2,47% in 2020 auf 1,28% in 2021 etwa halbiert. Die leichte Abnahme der Sterblichkeit bei den Altersgruppen 60-79 und 80+ ist mit großer Wahrscheinlichkeit ein Ergebnis der prioritären Impfung seit Anfang 2021. Rohdaten: RKI, Datenstand 22.01.2022.
Die Abnahme der Letalitätswerte gegenüber 2020 ist erwähnenswert, vor allem in der Altersgruppe 60-79, sie bleibt aber letztlich doch schwach ausgeprägt. Genau wie in der Altersgruppe 80+ dürfte dieser Rückgang auf die Wirkung der Impfung zurückzuführen sein. Dazu mehr weiter unten bei der Untersuchung der Sterblichkeitsraten für Geimpfte und Ungeimpfte. Die Letalität in den Altersgruppen 60-79 und 80+ bleibt aber dennoch auf hohem Niveau. Auffällig sind die extremen Unterschiede in den Letalitätsraten beim Vergleich zwischen den Älteren und den Jüngeren. Diesbezüglich hat sich zwischen 2020 und 2021 nahezu nichts geändert. Die Säulen für die Altersgruppen 0-19 (0,004%, also ein Fall pro 25.000 Infizierten) und 20-59 (0,014%, also 1 Fall pro 710 Infizierten) sind im Diagramm nicht bzw. gerade noch ansatzweise sichtbar.
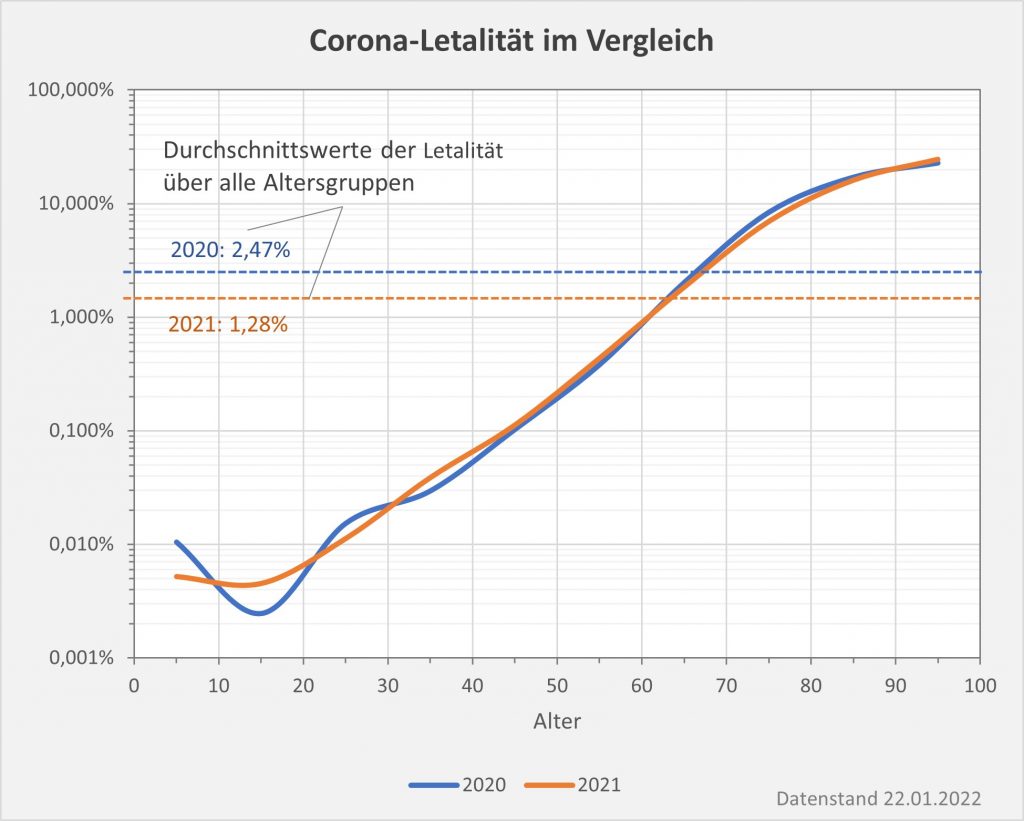
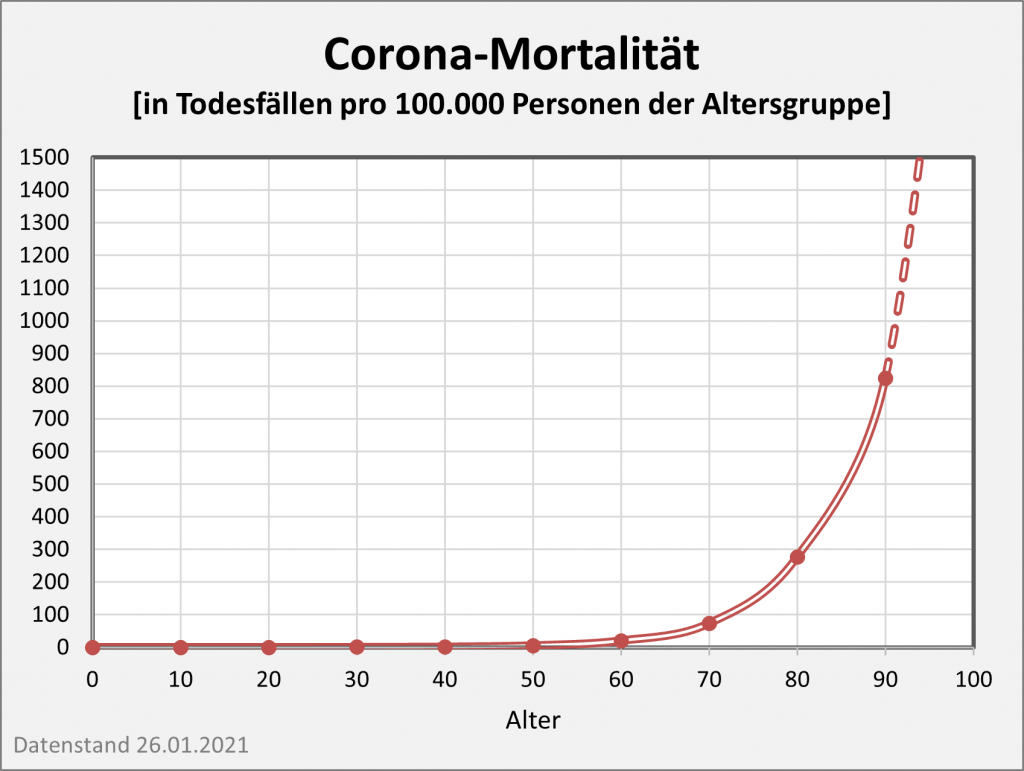
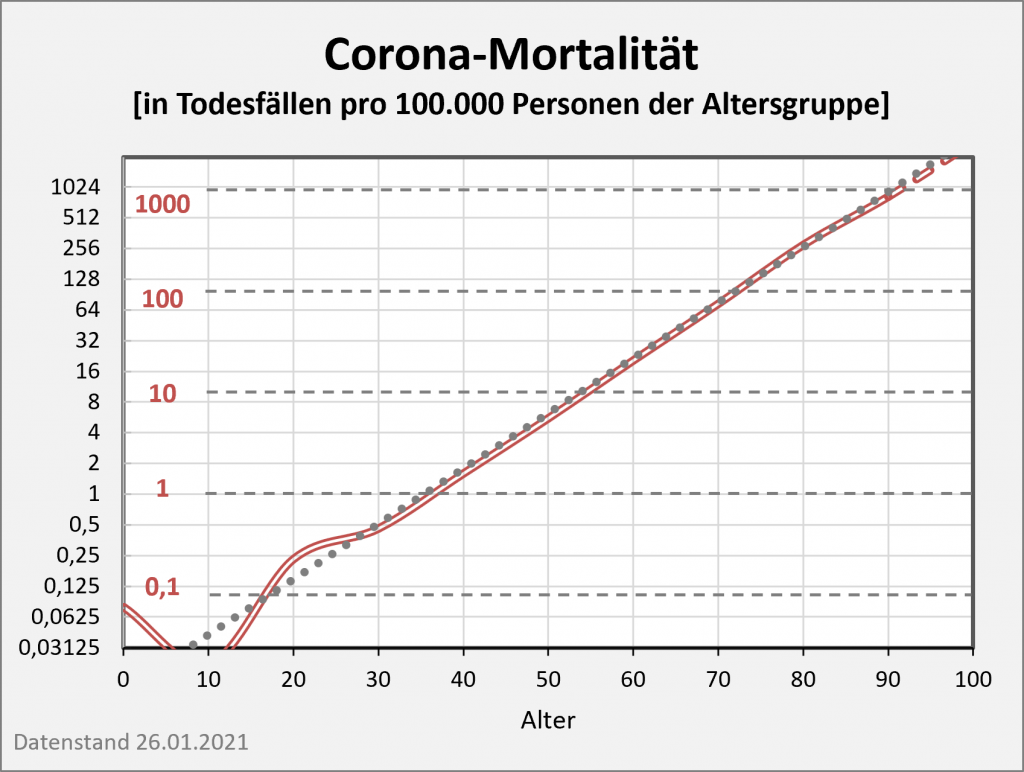
Abbildung 10: Kurvenverlauf der Covid-19-Letalität (Sterblichkeit nach einer Corona-Infektion) für 2020 und 2021 in Abhängigkeit vom Alter. Um die großen Unterschiede in den Sterblichkeitsraten zu veranschaulichen, wurde in der Darstellung eine logarithmische Skalierung gewählt. Im Lebensalter bis etwa 25 bewegen wir uns hier bei Letalitätswerten von 0,01% und darunter. Hingegen liegen die Sterblichkeitsraten für Lebensalter über 80 höher als 10%. In der Relation sind das in beiden Jahren etwa 1000-fach höhere Werte. Die Kurve für 2021 verläuft im oberen Bereich geringfügig flacher, was vermutlich auf die Wirkung der Impfkampagne zurückzuführen ist. Rohdaten: RKI, Datenstand 22.01.2022.
Der Vergleich der beiden Kurvenverläufe in Abb. 10 zeigt nochmals deutlich, dass sich in 2021 unter dem Gesichtspunkt der Sterblichkeit bei einer Corona-Infektion gegenüber 2020 kaum etwas geändert hat. Letztlich bleiben die Unterschiede jedenfalls gering. Die noch am meisten ins Auge fallenden Abweichungen bei den Unter-30-Jährigen sind in der Gesamtschau belanglos, weil wir hier von sehr niedrigen absoluten Risikoraten um 0,02% und darunter sprechen.
Tatsächlich größer (max. 1%) sind die Differenzen bei höherem Alter etwa zwischen 60 und 90. Der ab einem Alter von 60 gegenüber der 2020er Kurve partiell flachere Verlauf der Kurve für 2021 steht für einen geringeren Anstieg der Sterblichkeit in diesem Altersbereich. Allerdings zeigen sich auch die Grenzen: Bei den 90-Jährigen konnte auch der grundsätzlich positive Effekt der Impfung den Anstieg der Sterblichkeit nicht stoppen. Dabei liegt es auf der Hand: Die Impfung kann vor allem dort einen merklichen Effekt nach sich ziehen, wo das Risiko höher ist. Bei den Jüngeren mit den sehr niedrigen absoluten Risiken bleibt der Einfluss in der Gesamtschau vernachlässigbar.
Mortalität nach Altersgruppen – Vergleich 2020/2021
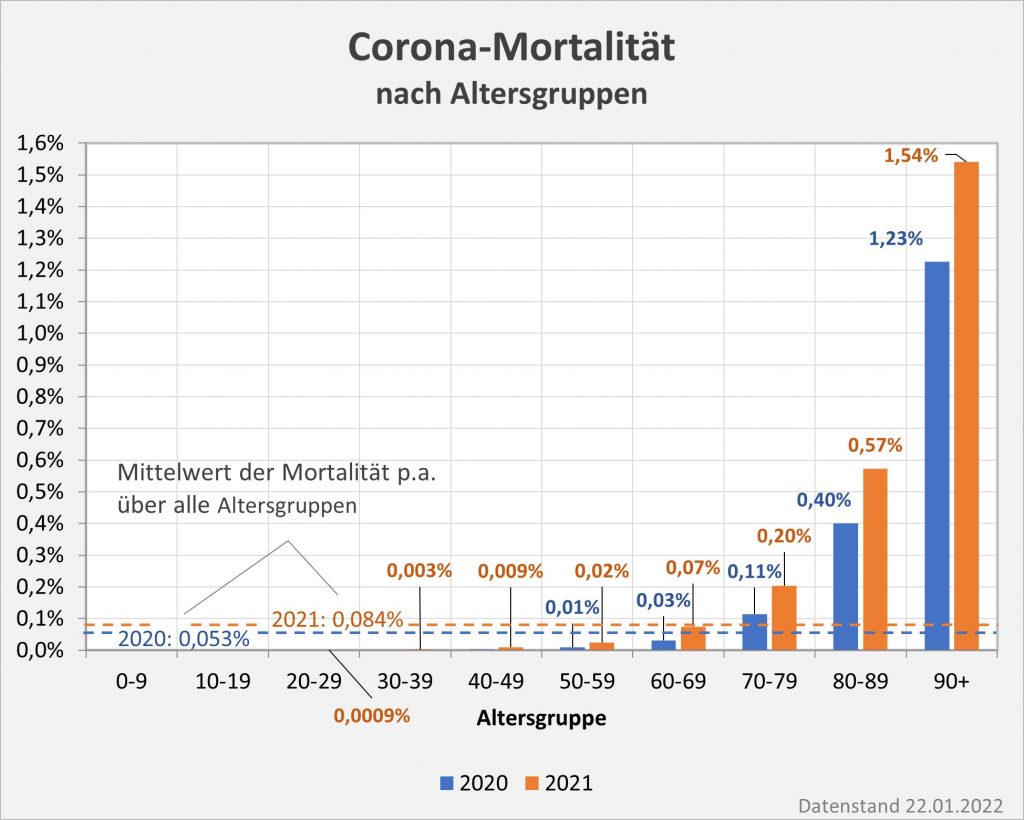
Abbildung 11: Covid-19-Mortalität (Sterblichkeit p.a.) für 2020 und 2021 nach Altersgruppen im Vergleich. Man sieht, dass die 2021er-Säulen stets etwas höher sind als die 2020er. Die Sterblichkeit aufgrund von Corona ist daher in 2021 gegenüber 2020 angestiegen. Die Größe des Effekts erkennt man anhand der mittleren Sterblichkeit über alle Altersgruppen: Sie hat sich von 0,053% in 2020 auf 0,084% in 2021 in der Relation um 59% erhöht. Diese ungünstige Entwicklung ist auf die stark angewachsenen Infektionszahlen zurückzuführen und spiegelt die Zunahme bei den Todesfallzahlen wider. Durch die im Jahresverlauf ohnehin noch nicht voll wirksame Impfung konnte der Anstieg nicht kompensiert werden (s. Text). Rohdaten: RKI, Datenstand 22.01.2022.
Wie man Abb. 11 entnimmt, ist die Corona-Sterblichkeit insbesondere in den Altersgruppen ab 50 gewachsen, teilweise durchaus signifikant. Für die Altersgruppen 80-89 liegt die Mortalität in 2021 bei 0,57%, in der Altersgruppe 90+ gar bei 1,54%. Damit hat sich die Sterblichkeit in der Spitze um 0,15% bis 0,3% gegenüber dem Wert für 2020 erhöht. In absoluten Zahlen macht das allein bezüglich der Altersgruppen 80-89 und 90+ fast 12.000 Sterbefälle mehr aus. In den Altersgruppen 40-49 bis hinunter zu 0-9 verbleibt die Mortalität hingegen im Wertebereich zwischen 0,009% und 0,0004% (also 1 Fall pro 11.000 in der Altersgruppe 40-49 bzw. 1 Fall pro 250.000 in der Altersgruppe 0-19). Im Diagramm sind diese Säulen skalierungsbedingt nicht mehr sichtbar.
Die Erhöhung der durchschnittlichen Sterblichkeit über alle Altersgruppen in 2021 ist also i. W. auf die nochmals gestiegenen Todesfallzahlen bei den Älteren zurückzuführen. Die Altersgruppen ab 60 und insbesondere ab 80 tragen zum weit überwiegenden Teil zu den Todesfällen bei. Auch die prioritäre Impfung der Älteren und die erzielte hohe Impfquote in dieser Altersgruppe konnte den beobachteten Anstieg der Mortalität nicht verhindern. Durch die Impfung wurde der Zuwachs zwar abgemildert, dies aber nicht so durchgreifend, wie man das zu Beginn des Jahres wohl erhofft hatte. Ein Grund dafür dürfte die relativ schnell nachlassende Schutzwirkung der Impfung sein. Dies spricht nicht grundsätzlich gegen die Impfung, es relativiert aber den zu erwartenden Effekt.
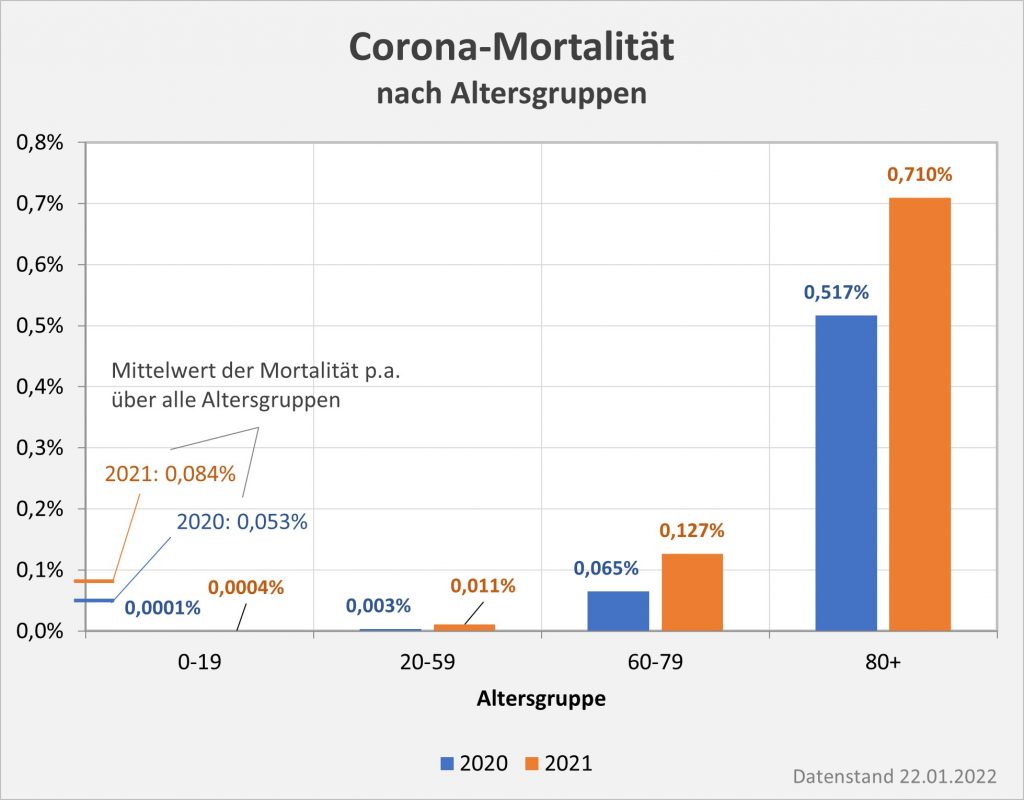
Abbildung 12: Covid-19-Mortalität (Sterblichkeit p.a.) für 2020 und 2021 in ausgewählten Altersgruppen im Vergleich. Die 2021er-Säulen sind stets etwas höher sind als die 2020er. Die Corona-Sterblichkeit ist daher in 2021 gegenüber 2020 angestiegen. Die größten relativen Zuwächse sind bei den Jüngeren zu verzeichnen. Im Hinblick auf die Sterblichkeit dominieren indessen die Altersgruppen 60-79 und 80+ mit riesigem Abstand. Das spiegelt die Erhöhung der absoluten Fallzahlen der Toten in 2021 wider (s. a. Abb. 4). Rohdaten: RKI, Datenstand 22.01.2022.
Der direkte Vergleich der Säulenhöhen in Abb. 12 zeigt in allen Altersgruppen einen Anstieg der Corona-Sterblichkeit p.a. Die relative Zunahme der Sterblichkeit ist dabei hinsichtlich der Altersgruppen unter 80 am stärksten ausgeprägt, wobei die Gruppen 0-19 und 20-59 aufgrund des absolut gesehen sehr niedrigen Risikos in Summe nicht ins Gewicht fallen. Anders sieht es aus in der Altersgruppe 60-79. Hier liegt der relative Zuwachs bei über 95%, was in absoluter Höhe immerhin eine Zunahme um 0,062% bedeutet. Bezüglich der Todesfallzahlen gehen über 11.000 Tote allein auf dieses Konto. Man kann vermuten, dass durch ein schnelleres Voranschreiten Impfung in der Altersgruppe 60-79 ein gewisser Anteil dieser Fälle hätte vermieden werden können (s. dazu die Diskussion zur weiter unten).
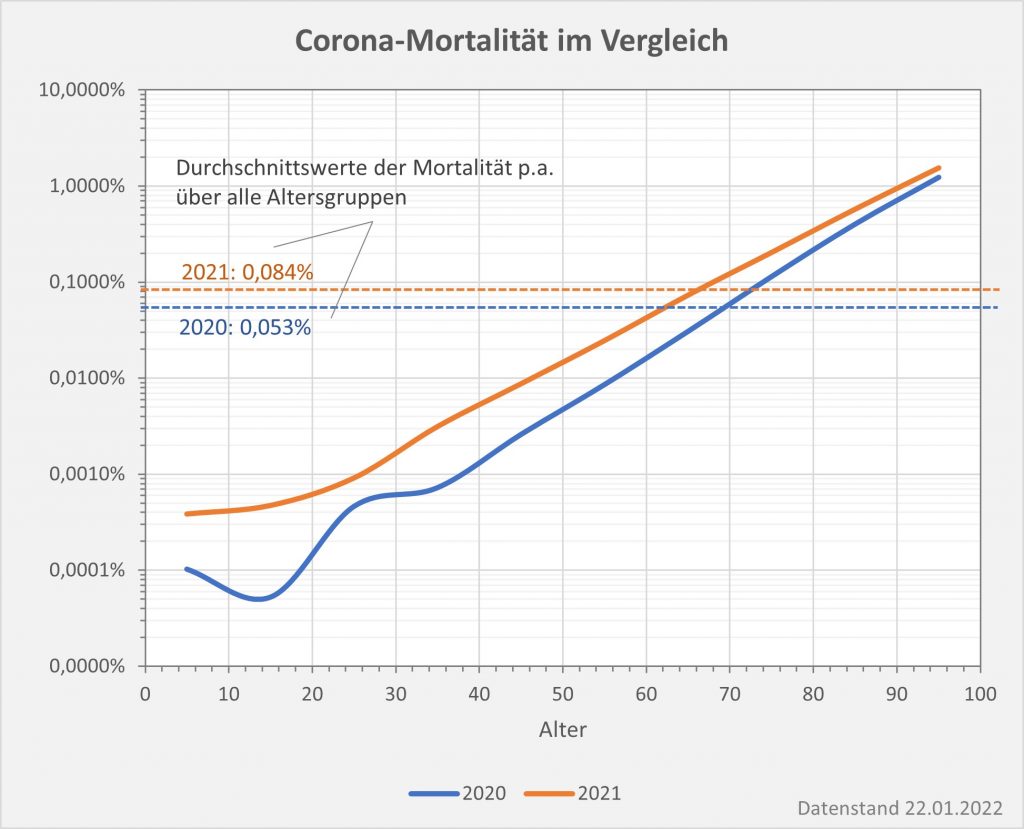
Abbildung 13: Kurvenverlauf der Covid-19-Mortalität (Sterblichkeit p.a.) für 2020 und 2021 in Abhängigkeit vom Alter. Um die großen Unterschiede in den Sterblichkeitsraten zu veranschaulichen, wurde in der Darstellung eine logarithmische Skalierung gewählt. Im Lebensalter bis etwa 25 bewegen wir uns hier bei Mortalitätswerten von 0,001% und darunter. Hingegen liegen die Sterblichkeitsraten für Lebensalter oberhalb 90 bei 1% und darüber. In der Relation sind das in beiden Jahren etwa 1000-fach höhere Werte. Im Vergleich zu 2020 verläuft die Kurve für 2021 insgesamt etwas flacher, was z. T. vermutlich auf die Wirkung der Impfkampagne zurückzuführen ist. Daneben haben aber vor allem die hohen Infektionszahlen bei den Jüngeren einen markanten Einfluss auf den flacheren Kurvenverlauf. Rohdaten: RKI, Datenstand 22.01.2022.
Der Vergleich der beiden Kurvenverläufe in Abb. 13 zeigt nochmals in aller Klarheit, dass in 2021 unter dem Gesichtspunkt der Gesamtsterblichkeit gegenüber 2020 kein wirklicher Fortschritt erzielt wurde. Im Gegenteil: Die Mortalität hat sich durchweg erhöht. Als Verbesserung kann man allenfalls den geringeren relativen Anstieg bei den Älteren konstatieren. Zumindest zum Teil dürfte dieses Resultat auf den risikosenkenden Effekt der Impfung zurückzuführen sein. Ohne die Impfung würde die Mortalität in den Altersgruppe 60+ und damit auch insgesamt sicher höher liegen. Im Rahmen der Diskussion zur Letalität von Geimpften und Ungeimpften wird dieses Szenario näher beleuchtet.
Detailanalyse zur Letalität nach Alter
Die obigen Kurvendarstellungen für die Letalität und die Mortalität über das Alter erlauben aufgrund der über weite Altersbereiche nahezu linearen Verläufe einfache Näherungsdarstellungen oder andere polynomiale Approximationen. In Abb. 14 ist der Kurvenverlauf der Letalität zusammen mit zwei Näherungskurven in Abhängigkeit vom Alter dargestellt. Erfreulicherweise kann man die effektive Letalität für einen weiten Bereich der interessierenden Lebensalter mittels einer (in logarithmischer Darstellung linear erscheinenden) Exponentialfunktion darstellen.
Die lineare Näherung bringt die entscheidende Aussage in aller Deutlichkeit zum Ausdruck:
Die Letalität steigt exponentiell mit dem Lebensalter.
Das Wesen der Corona-Pandemie liegt bei Lichte betrachtet nicht darin, dass das Virus sich exponentiell ausbreiten kann. Für die effektive Bekämpfung viel wichtiger ist die Erkenntnis des mit dem Alter exponentiell steigenden Risikos. Übersetzt heißt dies: Maßnahmen zur Eindämmung der Todesfallzahlen müssen dort ansetzen, wo die Fallzahlen auftreten. Also bei den Alten, nicht bei den Jungen oder gar bei Kindern. Der Hebel bei den Ersteren hat eine bis zu 1000-fache Übersetzung (s.u.). Umgekehrt ist bei Letzteren das Kosten-Nutzen-Verhältnis um denselben Faktor kleiner.
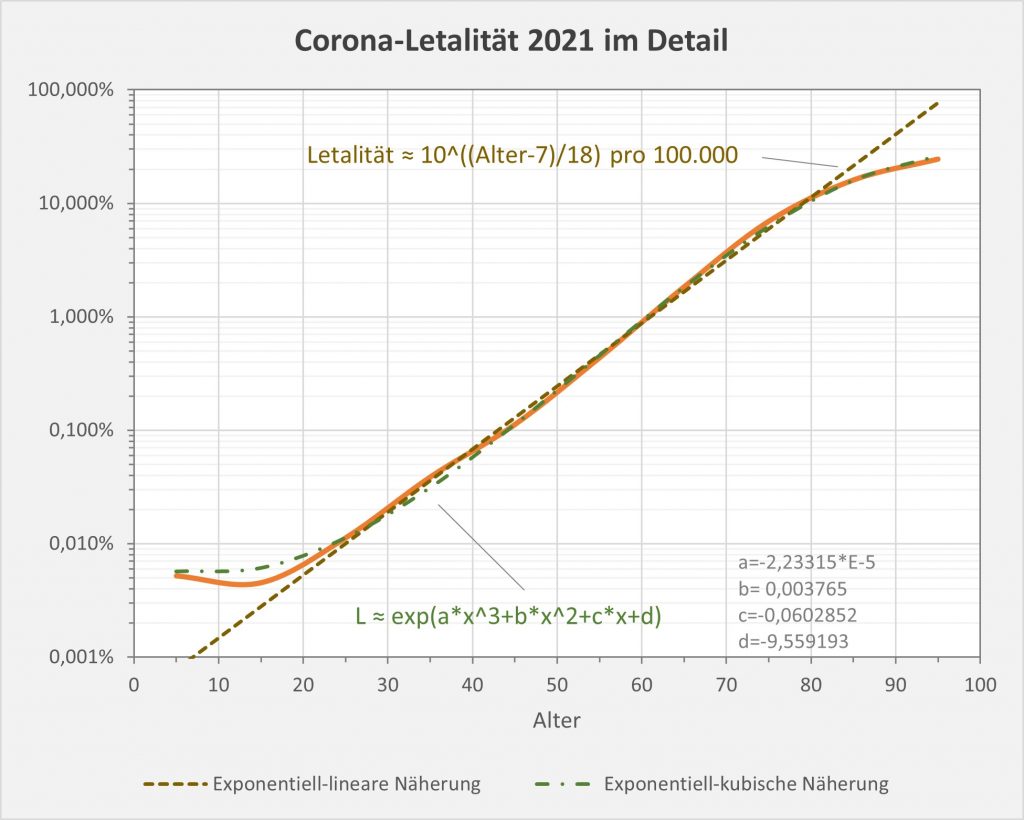
Abbildung 14: Kurvenverlauf der Covid-19-Letalität (Sterblichkeit nach Infektion p.a.) für 2021 in Abhängigkeit vom Alter. Man beachte die logarithmische Darstellung. Zusätzlich eingezeichnet sind zwei Näherungskurven: Eine exponentiell-lineare Näherung (gestrichelte Linie in braun) und eine exponentiell-kubische Näherung (strichpunktierte Linie in grün). Rohdaten zur Letalitätskurve: RKI, Datenstand 22.01.2022.
Ausgedrückt in Prozentwerten lautet die Formel für die Letalität:
Letalität ≈ 0,01% * 10^(Alter-25)/18
Nach vorstehender Approximationsformel verzehnfacht sich der Letalitätswert pro 18 Lebensjahren. Verglichen mit einem 24-Jährigen hat demzufolge ein 42-Jähriger ein 10-fach, ein 60-Jähriger ein 100-fach und ein 78-Jähriger ein 1000-fach höheres Corona-Sterberisiko p.a. bei vorliegender Corona-Infektion. Für die richtige Einordnung sollte man die Höhe des absoluten Risikos nicht unerwähnt lassen. Es liegt bei 0,008% p.a. für 24-Jährige und folglich bei etwa 8% p.a. für 78-Jährige.
Dargestellt als Zweierpotenz besagt die lineare Näherung Letalität ~ 2^(Alter/5,41). Daher kann man auch festhalten, dass sich die Corona-Sterblichkeit p.a. bei vorliegender Infektion pro etwa 5,5 Lebensjahren verdoppelt.
Weiteres s. Anhang.
Detailanalyse zur Mortalität nach Alter
Der Kurvenverlauf der Mortalität ist in Abb. 15 zusammen mit einer linearen Näherung in Abhängigkeit vom Alter dargestellt. Den tatsächlichen Verlauf kann man auch in diesem Falle durch eine Exponentialfunktion gut approximieren. Die lineare Näherung bringt das Grundsätzliche im Mortalitätsverlauf in aller Klarheit zum Ausdruck:
Die Mortalität wächst exponentiell mit dem Lebensalter.
Damit wird die obige Aussage zum Wesen der Corona-Pandemie auch im Hinblick auf die Mortalität unterstrichen. Die effektive Bekämpfung und Überwindung der Pandemie erfordert daher zielgenaue Maßnahmen, weil ansonsten die um mehrere Größenordnungen unterschiedlichen Risiken bei Älteren und Jungen in einen Topf geworfen und gleichartig behandelt werden. So erzielt man nur einen Bruchteil der möglichen Wirkung bei gleichzeitig maximalem Kosteneinsatz.
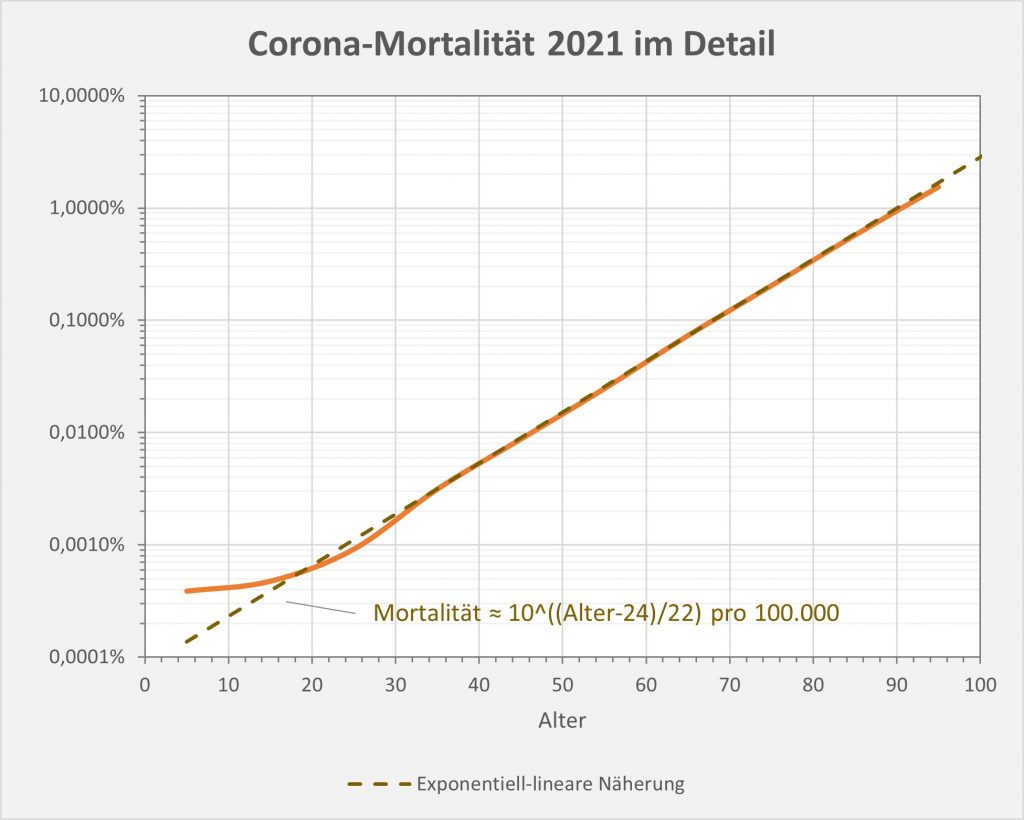
Abbildung 15: Kurvenverlauf der Covid-19-Mortalität (Sterblichkeit p.a.) für 2021 in Abhängigkeit vom Alter. Man beachte die logarithmische Darstellung. Zusätzlich eingezeichnet ist eine exponentiell-lineare Näherung (gestrichelte Linie in braun). Rohdaten zur Letalitätskurve: RKI, Datenstand 22.01.2022.
Ausgedrückt in Prozentwerten lautet die Formel für die Mortalität p.a.:
Mortalität ≈ 0,001% * 10^(Alter-24)/22
Nach dieser Approximationsformel verzehnfacht sich der Mortalitätswert p.a. pro 22 Lebensjahren. Verglichen mit einem 18-Jährigen hat demzufolge ein 40-Jähriger ein 10-fach, ein 62-Jähriger ein 100-fach und ein 84-Jähriger ein 1000-fach höheres Corona-Sterberisiko p.a.. Um das richtig einzuordnen, muss man erwähnen, dass das absolute Risiko von 18-Jährigen bei etwa 0,0005% liegt, das von 84%-Jährigen bei 0,5%.
Dargestellt als Zweierpotenz besagt die lineare Näherung Mortalität ~ 2^(Alter/6,62). Daher kann man konstatieren, dass sich das Corona-Sterberisiko p.a. bei vorliegender Infektion pro etwa 6,5 Lebensjahren verdoppelt.
Weiteres s. Anhang.
Detailanalyse zum Infektionsrisiko nach Alter
Der Kurvenverlauf des Infektionsrisiko ist in Abb. 16 zusammen mit zwei Näherungskurve in Abhängigkeit vom Alter dargestellt. Der Verlauf kann durch eine lineare Näherung nicht gut approximiert werden. Es geht hier eher darum, das grundsätzliche Verhalten im Verlauf des Infektionsrisikos in eine einfache Formel zu fassen. Für weite Altersbereiche ist die Abweichung vom tatsächlichen Verlauf nicht allzu groß. Die kubische Approximation ist insbesondere für die interessierenden Lebensalter ab 45 sehr viel präziser, aber natürlich auch unhandlicher. Das Wesentliche kommt bereits durch die lineare Näherung zum Ausdruck.
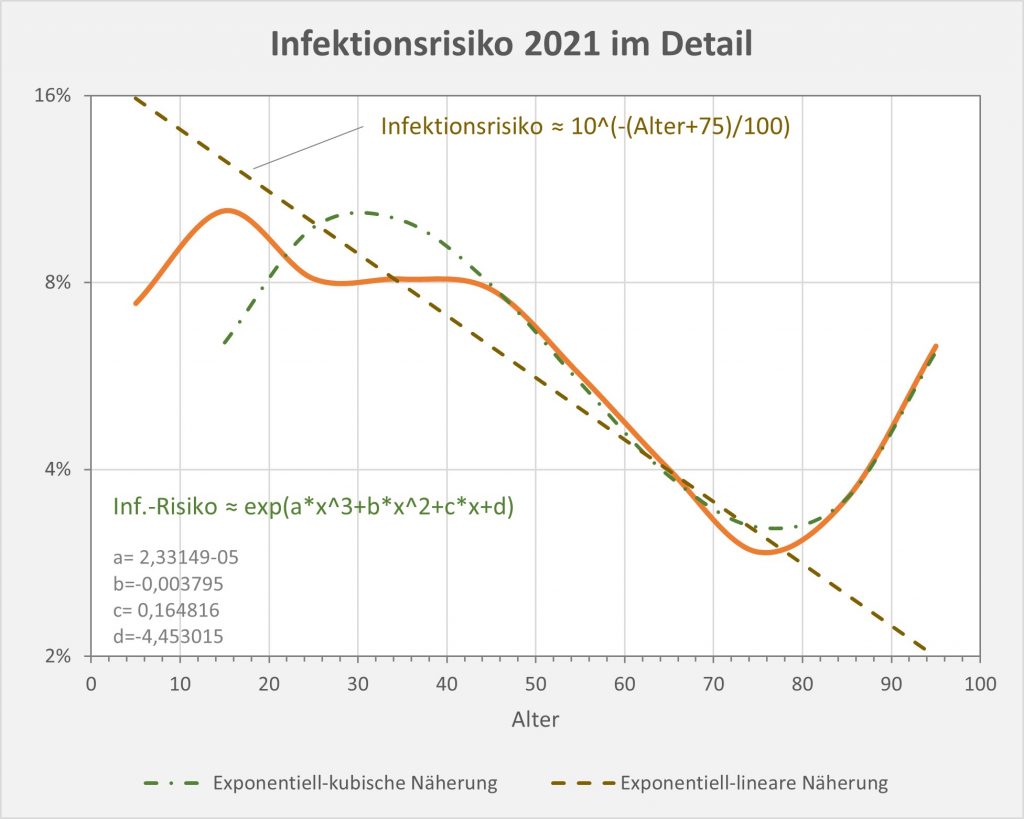
Abbildung 16: Kurvenverlauf des Covid-19-Infektionsrisikos (Infektionswahrscheinlichkeit p.a.) für 2021 in Abhängigkeit vom Alter. Man beachte die logarithmische Darstellung. Zusätzlich eingezeichnet sind zwei Näherungskurven: Eine exponentiell-lineare Näherung (gestrichelte Linie in braun) und eine exponentiell-kubische Näherung (strichpunktierte Linie in grün). Rohdaten zur Letalitätskurve: RKI, Datenstand 22.01.2022.
Ausgedrückt in Prozentwerten lautet die Formel für das Infektionsrisiko p.a.:
Infektionsrisiko ≈ 10% * 1/10^(Alter-25)/100
Im Unterschied sowohl zur Letalität wie auch zur Mortalität, die beide mit zunehmendem Alter exponentiell wachsen, sehen wir bezüglich des Infektionsrisikos ein gegenteiliges Verhalten: Je höher das Alter, desto geringer die Infektionswahrscheinlichkeit. Diese Abhängigkeit ist zwar nicht so stark und eindeutig ausgeprägt, sie führt aber dennoch dazu, dass das Infektionsrisiko mit dem Alter signifikant zurückgeht. Vermutlich deswegen, weil die Anzahl der Kontakte gleichfalls sinkt.
Ganz grob kann man sagen, dass sich die Infektionswahrscheinlichkeit p.a. pro 30 Lebensjahren in etwa halbiert. Ein Blick auf die Zweierpotenz-Näherungsformel macht das unmittelbar klar.
Infektionsrisiko ≈ 12,5% * 1/2^(Alter-15)/30
Weiteres s. Anhang.
Berechnung der Letalität für Geimpfte und Ungeimpfte nach Altersgruppen
Die Letalitätswerte pro Altersgruppe haben wir oben aus den Daten des RKI abgeleitet und diskutiert. Eine Unterscheidung in Geimpfte und Ungeimpfte kann daraus nicht unmittelbar abgeleitet werden, da die Impfstatus der Infizierten und der Verstorbenen in 2021 nicht konsequent erfasst wurden (jedenfalls wurden diese Zahlen vom RKI nicht veröffentlicht). Über einen kleinen Umweg ist es indessen möglich, die Zahl der infizierten und verstorbenen Geimpften, und
, indirekt zu berechnen. Gleiches geht natürlich auch für die Ungeimpften (
und
).
Das Rechenverfahren mit der Herleitung der nötigen Formeln wird im Anhang näher dargestellt. Die Datengrundlage für die angenommenen altersgruppenspezifischen Impfquoten und Wirksamkeiten ist in Tab. 1 aufgelistet.
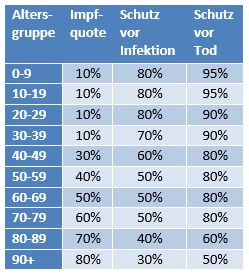
Tabelle 1: Annahmen zu den altersgruppenspezifischen Impfquoten und den Schutzwirkungen der Impfung im Hinblick auf eine Covid-19-Infektion und Tod (an oder mit Corona). Die durchschnittlichen Impfquoten ergeben sich aus dem Verlauf der Impfkampagne im Jahresverlauf aus den Daten des RKI. Die Annahmen zur Schutzwirkung basieren auf den Infektionszahlen Geimpfter und Ungeimpfter (wurden in der zweiten Jahreshälfte für symptomatisch Erkrankte erfasst). Hinsichtlich des Schutzes vor Tod wurden die Todesfallzahlen des RKI in den Kalenderwochen 40-49/2021 zugrunde gelegt. Ferner wurden Studienaussagen über das Nachlassen der Schutzwirkung in den Monaten nach der zweiten Impfdosis berücksichtigt (s. [8]).
Abbildung 17 zeigt die Ergebnisse der Berechnung auf Basis der angenommenen Jahresmittelwerte für die Impfquoten und die Wirksamkeiten (s. Tab. 1).
Folgende Formeln wurden angewendet (s. Anhang):
Berechnung der Letalität für Geimpfte:
(1)
Berechnung der Letalität für Ungeimpfte:
(2)
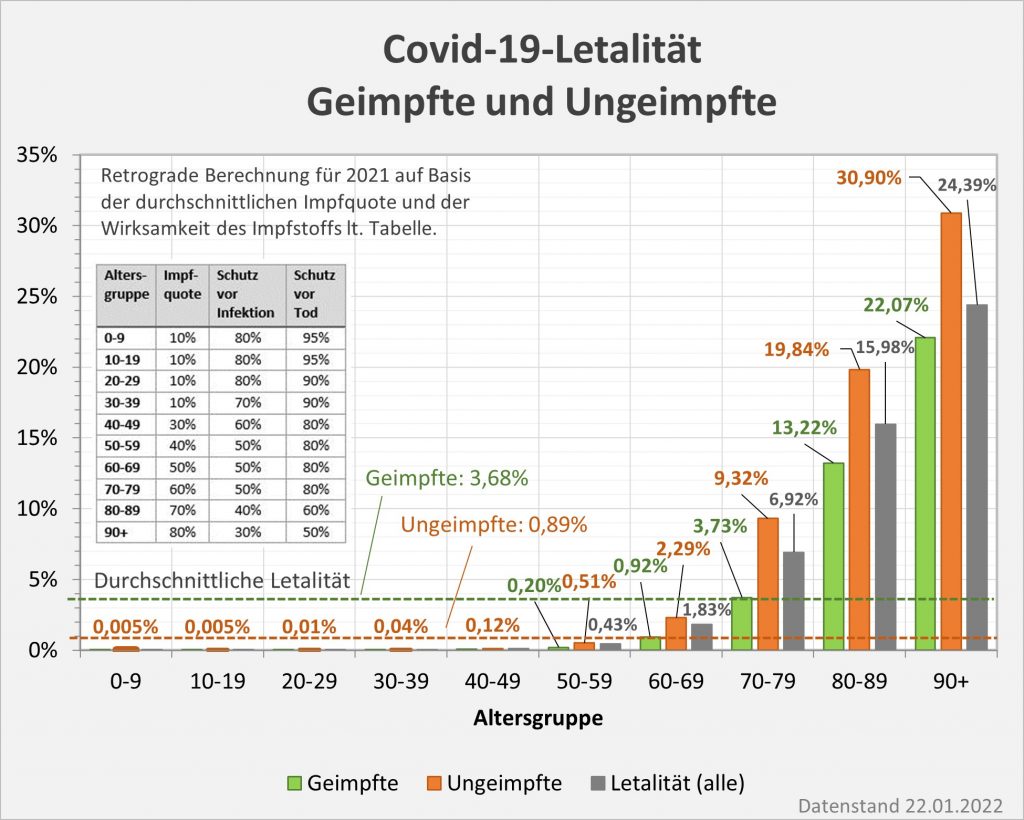
Abbildung 17: Berechnete Covid-19-Letalität (Sterblichkeitsrate nach einer Corona-Infektion) in 2021 für Geimpfte und Ungeimpfte nach Altersgruppen. Die grauen Säulen zeigen die mittlere Sterblichkeit pro Altersgruppe. Man erkennt, dass die Sterblichkeitsraten von Geimpften in den interessierenden und am meisten gefährdeten Altersgruppen 60-69, 70-79 80-89 und 90+ gegenüber den jeweiligen Referenzwerten (graue Säulen) gesunken sind. Die Letalität der Ungeimpften liegt dagegen überall höher. Der Unterschied zwischen Geimpften und Ungeimpften macht in der Relation z.T. mehr als 100 % aus. Die mittlere Sterblichkeit über alle Altersgruppen liegt natürlich nach wie vor bei 1,28 %. Rohdaten: RKI, Datenstand 22.01.2022.
Die mittlere Letalität der Geimpften liegt nach den berechneten Daten bei etwa 3,68%, die der Ungeimpften bei 0,89%. Unter den Geimpften ist demnach die Sterblichkeit im Mittel 4-mal höher. Das erscheint auf den ersten Blick paradox und absolut unplausibel. Indessen lässt sich dieser Effekt sehr leicht erklären. Wie man Tab. 1 entnimmt und wie es ja auch der Realität entspricht, war die Impfquote bei den Älteren ab 60 im Jahresmittel deutlich höher als die Impfquote bei den Jüngeren (Altersgruppen, 0-9, 10-19, 20,29, 30-39, sogar 40.49). Die Ungeimpften rekrutieren sich daher zu einem großen Teil aus diesen zwar nicht geimpften, aber absolut ungefährdeten Altersgruppen, die zu den Todesfallzahlen in Summe weniger als 1% beitragen. Umgekehrt sind gerade die vulnerablen Gruppen geimpft – und sie haben natürlich trotz der Impfung immer noch ein vielfach höheres Corona-Sterberisiko als die jungen Ungeimpften.
Wir haben oben gesehen, dass sich die Letalität (also die Sterblichkeit bei einer vorliegenden Infektion) pro 18-Lebenjahren verzehnfacht. Wenn nun andererseits die Impfung im Idealfall eine Wirksamkeit von 90% entfaltet, dann wird dieser positive Schutzeffekt im Ergebnis pro 18-Lebensjahren Unterschied aufgezehrt. Demnach hat also z.B. ein 24-Jähriger Ungeimpfter immer noch ein 100-fach geringeres Risiko an Corona zu versterben als ein 78-Jähriger Geimpfter. Tatsächlich ist die Schutzwirkung der Impfung in der Realität gerade für die Ältesten deutlich geringer als 90%, teilweise geht sie eher in Richtung 50%. Deswegen kann es nicht verwundern, dass die Sterblichkeitsrate der Geimpften im Schnitt höher liegt als die der Ungeimpften.
Im Wesentlichen geht es hier um einen statistischen Effekt aufgrund der ungleichen Risikomischung in den beiden Gruppen. Der entscheidende Punkt ist die gewichtete Mittelwertbildung mit den jeweiligen Anteilen unter den Geimpften bzw. Ungeimpften in der Bevölkerung. Vorausgesetzt, die Impfquote in allen Altersgruppen wäre gleich (also gleiche Risikomischung), dann würde die Letalität der Geimpften auch in der Mittelwertbildung über alle Altersgruppen kleiner ausfallen als die der Ungeimpften.
Hypothetische Todesfallzahlen auf Basis der berechneten Letalitätswerte für Geimpfte und Ungeimpfte
Auf Basis der berechneten Letalitätswerte für Geimpfte und Ungeimpfte kann man grob bestimmen, wie hoch die Todesfallzahlen in 2021 gewesen wären, wenn niemand oder alle geimpft gewesen wären. Natürlich ist dieser Ansatz in gewisser Weise spekulativ, weil man nicht sicher vorhersagen kann, welchen Einfluss eine geänderte Impfquote auf die Infektionsfallzahlen gehabt haben würde. Nach allem, was wir heute wissen, kann man in erster Näherung davon ausgehen, dass dieser Einfluss eher gering ist. Nach den Daten des RKI zu den symptomatischen Covid-19-Fällen, tragen Geimpfte und Ungeimpfte in ähnlichem Grade zum Infektionsgeschehen bei. Geimpfte sind demzufolge, schon wegen ihrer zahlenmäßigen Dominanz, nicht wegzudenkende Treiber der Infektionsdynamik. Unterstellen wir daher in einer ersten Betrachtung, es gebe durch die Impfung keine unmittelbare Rückwirkung auf die Inzidenzen. Wie hoch wären unter dieser Annahme die Todesfallzahlen für 2021 in den beiden Extremszenarien ausgefallen?
In Abb. 18 sind die entsprechenden, auf Basis der berechneten Letalitätswerte und der geschilderten Annahme bestimmten hypothetischen Todesfallzahlen im Vergleich zu den tatsächlichen Fallzahlen nach Altersgruppen getrennt hintereinander dargestellt.
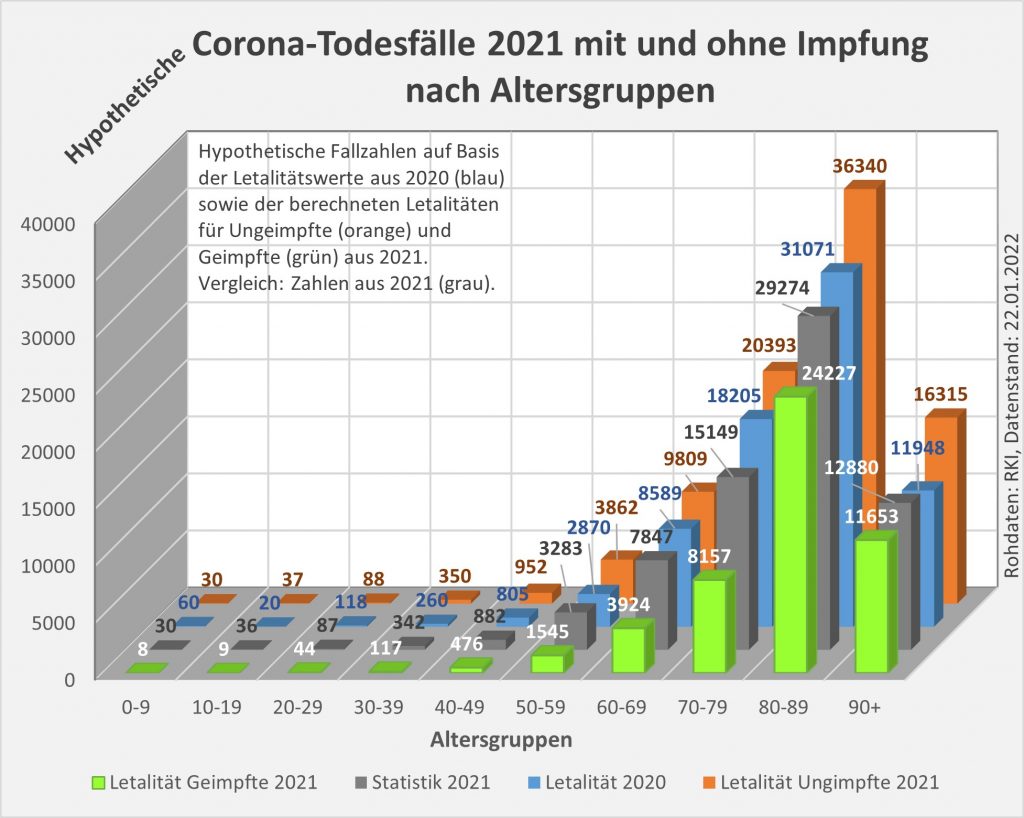
Abbildung 18: Tatsächliche und hypothetische Todesfallzahlen für 2021 bei unterschiedlichen Annahmen. Die Reihenfolge der Legende entspricht der Höhe der Säulen von vorne nach hinten. Die grünen Säulen im Vordergrund zeigen die Todesfallzahlen unter der Annahme, alle seien schon zu Beginn des Jahres geimpft (Impfquote 100%) gewesen und würden die Sterblichkeitsrate in Höhe der berechneten Letalität aufgewiesen haben. Im Hintergrund orange dargestellt sind die Säulen für das Alternativszenario ganz ohne Impfung (Impfquote 0%). Die tatsächlichen Fallzahlen werden durch die grauen Säulen aufgezeigt. Zusätzlich dargestellt sind die hypothetischen Fallzahlen unter der gleichfalls nicht abwegigen Annahme, die Letalitätswerte aus 2020 würden auch in 2021 zutreffend gewesen sein (blauen Säulen). Rohdaten: RKI, Datenstand 22.01.2022.
In der Gesamtschau macht Abb. 18 klar, dass die Impfung die Fallzahlen in allen Altersgruppen ab 60 merklich verringert. Umgekehrt würde der völlige Verzicht auf die Impfung in genau diesen Altersgruppen für eine signifikante Erhöhung der Fallzahlen gesorgt haben. Keinen nennenswerten Effekt sieht man bei den Altersgruppen unter 50, einen geringen in der Altersgruppe 50-59.
Die Summenwerte der Todesfallzahlen für die vier Szenarien sind in Abb. 19 dargestellt.
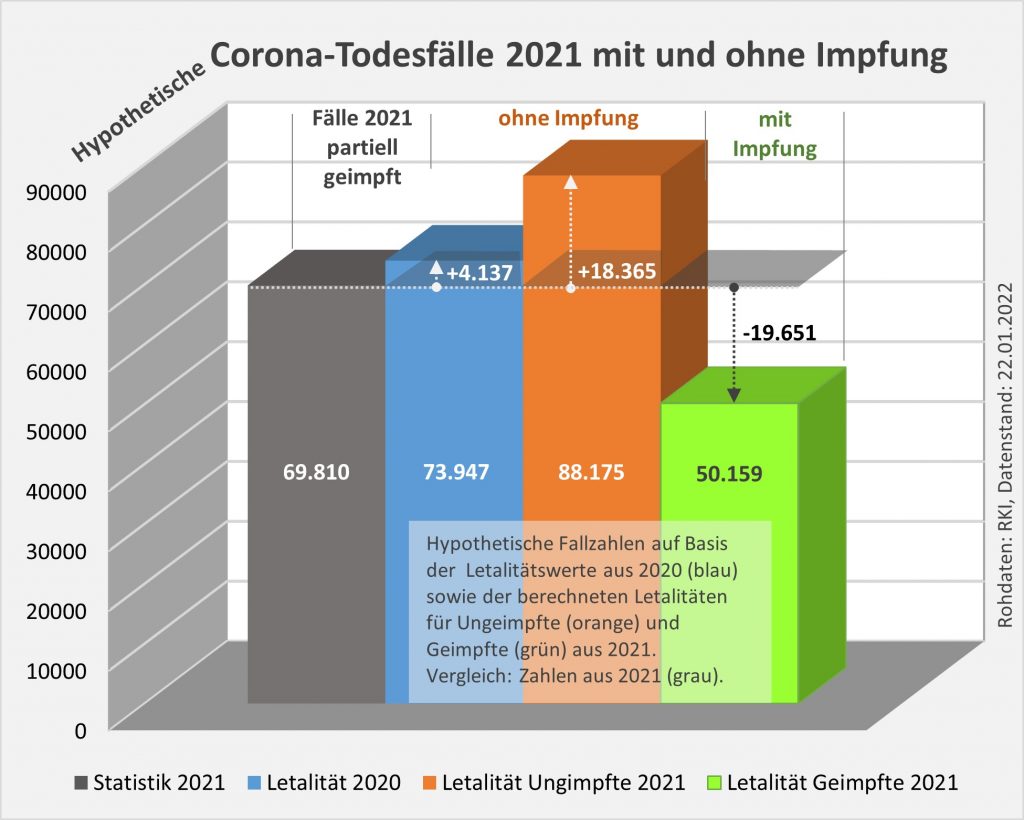
Abbildung 19: Tatsächliche und hypothetische Todesfallzahlen für 2021 in unterschiedlichen Szenarien. Die Grafik zeigt die Summenwerte der Todesfallzahlen für die vier betrachteten Szenarien. Grün: alle schon zu Beginn des Jahres geimpft (Impfquote 100%), Sterblichkeitsrate in Höhe der berechneten Letalität. Orange: Alternativszenario ganz ohne Impfung (Impfquote 0%). Grau: Tatsächliche Fallzahlen in 2021. Blau: Hypothetische Fallzahlen unter der Annahme, die Letalitätswerte aus 2020 würden auch in 2021 gegolten haben. Rohdaten: RKI, Datenstand 22.01.2022.
Das blaue (Sterblichkeit 2020 auch in 2021) und das orange Szenario (berechnete Sterblichkeit für Ungeimpfte aus den 2021-er Daten) belegen, dass die partielle Impfung in 2021 wohl eine Wirkung entfaltet hat. Jedenfalls würden die Fallzahlen ohne die Impfung mit einiger Wahrscheinlichkeit um einen hohen vierstelligen bis niedrigen 5-stelligen Zahlenwert höher ausgefallen sein. Auch wenn die Szenarien die Realität nicht 1:1 widerspiegeln mögen, so geben sie doch einen validen Hinweis. Das gilt auch für die Grenzen im Hinblick auf die Höhe des zu erwartenden Resultats.
Die beiden Szenarien „blau“ und „orange“ sind im Ergebnis nicht deckungsgleich. Das war aufgrund der höheren Gefährdung durch die in 2021 verbreitete Delta-Variante auch nicht zu erwarten. Sie weisen aber in dieselbe Richtung. Das stützt die Sinnhaftigkeit des beschriebenen Ansatzes (s. Anhang) zur separaten Ableitung der Letalitätswerte für Geimpfte und Ungeimpfte. Der Vergleich der tatsächlichen Fallzahlen mit dem grünen Szenario zeigt überdies den möglichen Effekt einer hohen Impfquote. Die Fallzahlen gehen sicher nicht auf Null, das ist angesichts der begrenzten und im Zeitverlauf rasch nachlassenden Wirksamkeit der verfügbaren Impfstoffe auch nicht zu erwarten. Dennoch ist die mögliche Reduzierung der Anzahl der Todesfälle signifikant, wenn auch nicht durchschlagend.
Hypothetische Todesfallzahlen bei Änderung der Impfquote
Im vorstehenden Abschnitt haben wir den Aspekt der Infektionszahlen außer Acht gelassen. Deswegen müssen die Ergebnisse zunächst als Fingerzeige gelten. Es ist indessen möglich, die Auswirkungen einer geänderten Impfquote und oder einer anderen Wirksamkeit des Impfstoffes mit einer etwas höheren Präzision aus den Felddaten abzuleiten. Dabei gehen wir von folgenden Überlegungen aus:
Eine Veränderung der Impfquote hat Einfluss auf die Anzahl der Geimpften und Ungeimpften und damit auch auf die Infektionszahlen. Die Sterblichkeit sowohl unter den Geimpften wie auch den Ungeimpften berührt das aber in erster Näherung nicht. Daher erscheint die Annahme konstanter Letalitätswerte pro Altersgruppe plausibel. Anders verhält es sich bezüglich der (Gesamt-)Letalität über alle Infizierten. Wenn die Impfquote modifiziert wird oder sich der Infektionsschutz verändert, dann verschieben sich auch die relativen Anteile der Geimpften und Ungeimpften unter den Infizierten und in der Folge auch das Verhältnis zwischen den Todesfallzahlen. Daher wird die (Gesamt-)Letalität bei der beschriebenen Änderung in der Regel nicht gleichbleiben.
Ausgangspunkt für die Ableitung der Formelbeziehungen ist das Invarianz-Postulat:
- Die altersgruppenspezifischen Letalitätswerte der Geimpften und der Ungeimpften sind invariant hinsichtlich einer Modifikation der Impfquote und / oder einer Veränderung der Wirksamkeit des Impfstoffs im Hinblick auf den Schutz vor Infektion (vorausgesetzt, der Todesfallschutz bleibt gleich).
Die mathematischen Überlegungen finden sich im Anhang.
Folgende Formeln kommen für die Bestimmung der Todesfallzahlen bei modifizierter Impfquote und/oder Wirksamkeit
zur Anwendung.
Anzahl der Fälle unter Ungeimpften pro Altersgruppe:
(3)
Anzahl der Fälle unter Geimpften pro Altersgruppe:
(4)
Neue (Gesamt-)Letalität pro Altersgruppe:
(5)
Gesamtanzahl der Fälle pro Altersgruppe:
(6)
Sofern die Wirksamkeit unverändert bleibt:
(7)
Die erzielten Ergebnisse für insgesamt 7 unterschiedliche Szenarien mit altersgruppenspezifisch variierten Impfquoten finden sich in den Abbildungen 20 und 21.
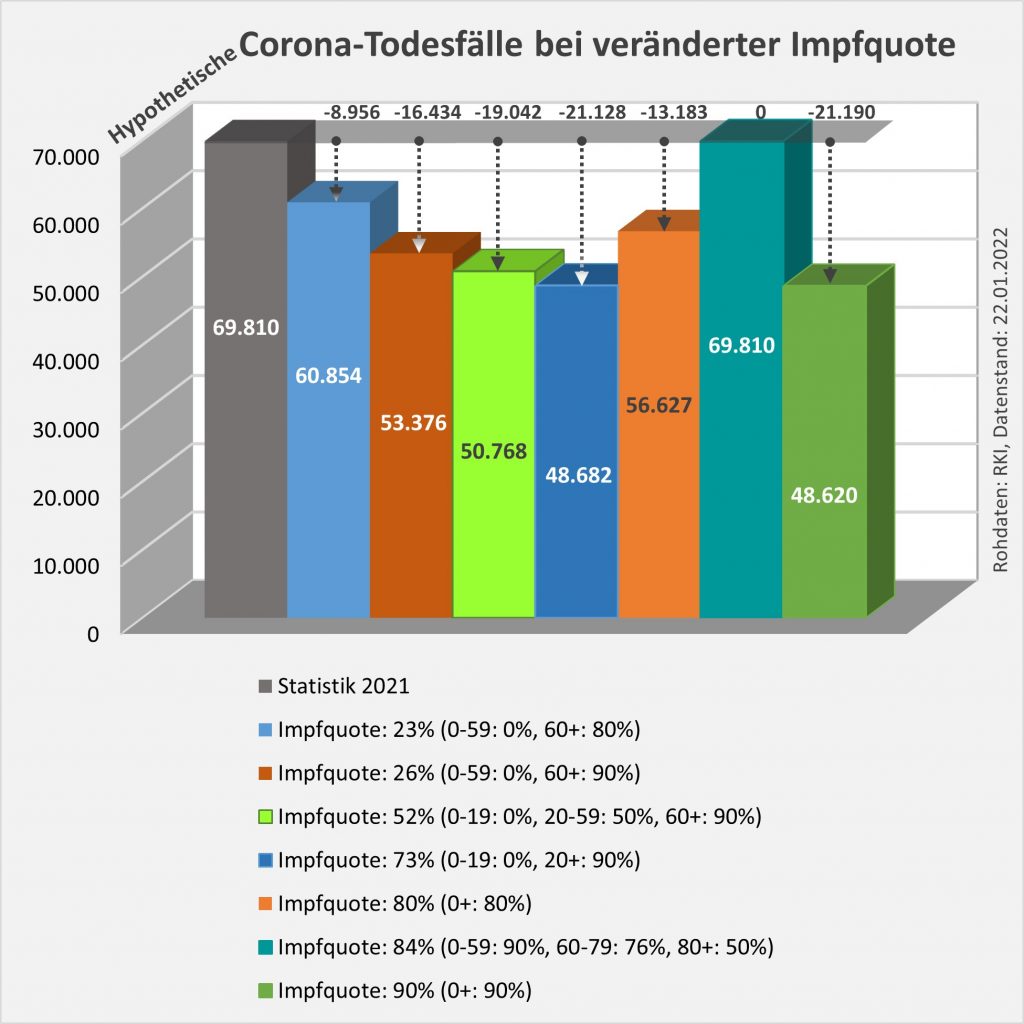
Abbildung 20: Tatsächliche und hypothetische Todesfallzahlen für 2021 bei unterschiedlichen Annahmen zur Höhe der Impfquote. Die Grafik zeigt die Summenwerte der Todesfallzahlen für sieben unterschiedliche Szenarien betreffend der Impfquoten über die Altersgruppen. Zum Vergleich sind die tatsächlichen Fallzahlen aus 2021 (Rubrik ganz links) aufgeführt. Die Säulen sind von links nach rechts nach der Höhe der Gesamtimpfquote geordnet. Ganz oben sind die jeweiligen Differenzen der Fallzahlen zum Vergleichswert aus 2021 notiert. Rohdaten: RKI, Datenstand 22.01.2022.
Man sieht, dass die Höhe der Impfquote allein nur eine begrenzte Aussagekraft im Hinblick auf die erzielbare Reduzierung der Fallzahlen besitzt. Die zweite Rubrik von rechts steht für eine Impfquote von 85%, dennoch liegen die Todesfallzahlen gleich hoch wie in 2021. Warum? Es sind die Falschen geimpft. Nicht die Alten, sondern die Jungen. Umgekehrt kann man mit einer Impfquote von nur 52% (hellgrüne Säule, vierte Rubrik von links) eine Verringerung der Anzahl der Todesfälle auf einem ähnlichen Niveau erzielen, wie das im Szenario mit 73% Impfquote (dunkelbaue Säule, fünfte Rubrik von links) oder im Szenario mit 90% Impfquote (grüne Säule, Rubrik ganz rechts) möglich ist. Entscheidend ist die Durchimpfung von den höheren zu den niedrigeren Altersgruppen.
In der letzten Grafik wird für die Fallzahlen in den betrachteten Szenarien zusätzlich die Unterscheidung in Geimpfte und Ungeimpfte vorgenommen. Dies wirft noch einmal ein Schlaglicht auf die Grenzen des durch eine hohe Impfquote Erreichbaren im Hinblick auf die am Ende verbleibenden Todesfallzahlen unter Ersteren. Anderes als manche das meinen, gehen die Fallzahlen nicht auf null, wenn es keine Ungeimpften mehr gibt. Die Todesfallinzidenzen reduzieren sich auch nicht auf 10 %, weil die angegebene Impfstoffwirksamkeit von 90 % eher ein theoretischer Wert ist, der z.B. aufgrund der nachlassenden Schutzwirkung in der Praxis nicht erreicht wird.
Ohne Zweifel hat eine hohe Impfquote einen bedeutsamen Effekt auf die Verringerung der Fallzahlen. Es bleibt aber immer noch eine beträchtliche und mit den verfügbaren Impfstoffen offenbar nicht weiter reduzierbare Anzahl von Sterbefällen, weil mit der Impfquote natürlich auch die Todesfallzahlen unter den Geimpften ansteigen. In Abb. 21 sieht man das ganz deutlich. Das spricht nicht gegen die Impfung, denn die Gesamtanzahl der Corona-Todesfälle geht auf jeden Fall zurück. Es relativiert aber den erwartbaren Erfolg.
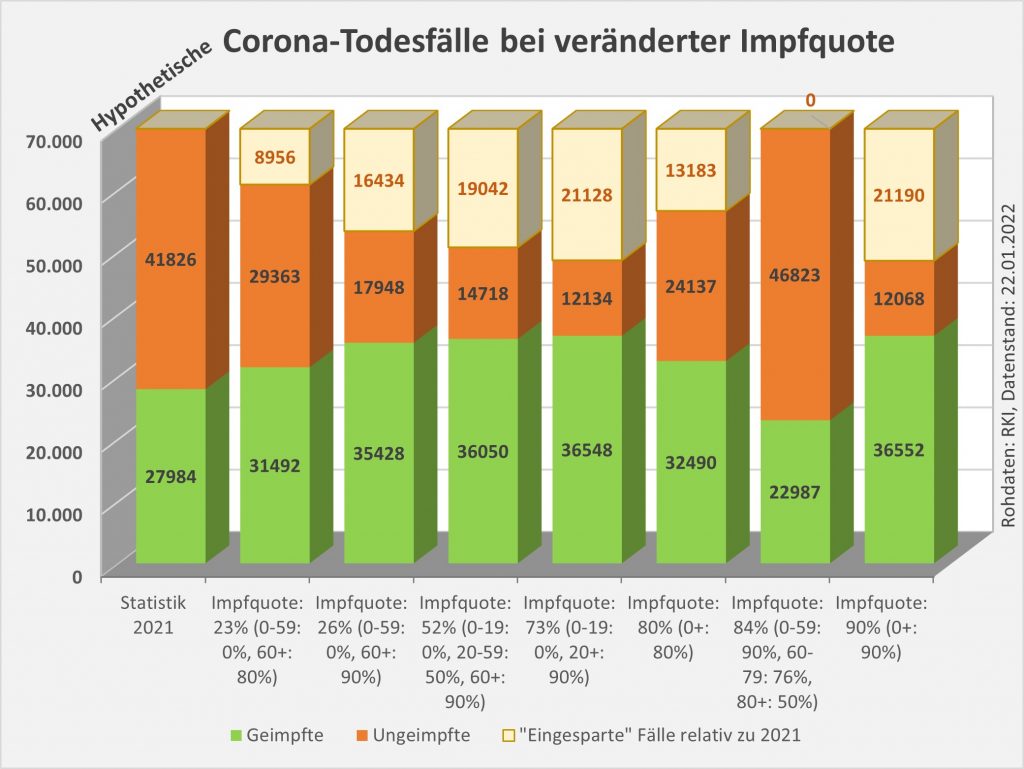
Abbildung 21: Tatsächliche und hypothetische Todesfallzahlen (Geimpfte und Ungeimpfte) für 2021 bei unterschiedlichen Annahmen zur Höhe der Impfquote. Die Grafik zeigt die Summenwerte der Todesfallzahlen für sieben unterschiedliche Szenarien betreffend der Impfquoten über die Altersgruppen. Die Säulen sind von links nach rechts nach der Höhe der Gesamtimpfquote geordnet. Grün: Anzahl der Todesfälle bei Geimpften. Orange: Todesfälle bei Ungeimpften. Orange-weiß: Verringerung der Gesamtfallzahlen im Vergleich zu den tatsächlichen Werten aus 2021 (Rubrik ganz links). Rohdaten: RKI, Datenstand 22.01.2022.
Mathematischer Anhang
Die altersabhängige Corona-Sterblichkeit bei Infektion (Letalität)
Die Letalität pro 100.000 Infizierten kann durch die folgende exponentiell-lineare Näherungsformel ausgedrückt werden:
(8)
Ausgedrückt in Prozentwerten lautet die Formel für die Letalität:
(9)
Für den Altersbereich 5-80 bleibt der absolute Fehler unter 0,25%. Der relative Fehler liegt für die Altersgruppe 20-80 meist unter 5%. Es gibt zwei Ausreißer mit einer Überschätzung des Risikos für die Altersgruppen 40-49 (30%) und 50-59 (22%).
Nach obiger Approximationsformel verzehnfacht sich der Letalitätswert pro 18 Lebensjahren. Verglichen mit einem 24-Jährigen hat demzufolge ein 42-Jähriger ein 10-fach, ein 60-Jähriger ein 100-fach und ein 78-Jähriger ein 1000-fach höheres Corona-Sterberisiko p.a. bei vorliegender Corona-Infektion. Für die richtige Einordnung sollte man die Höhe des absoluten Risikos nicht unerwähnt lassen. Es liegt bei 0,008% p.a. für 24-Jährige und folglich bei etwa 8% p.a. für 78-Jährige.
Dargestellt als Zweierpotenz ergibt sich . Daher kann man festhalten, dass sich das Corona-Sterberisiko p.a. bei vorliegender Infektion pro etwa 5,5 Lebensjahren verdoppelt.
Eine bessere Approximation an den Letalitätsverlauf bietet die nachstehende exponentiell-kubische Näherungsformel:
(10)
Für den Altersbereich 5-95 bleibt der absolute Fehler bis auf zwei Ausnahmen für die Altersgruppe 70-79 (0,65%) und 90+ (2,6%) unter 0,02%. Der relative Fehler ist für die Altersgruppen 20-29, 40-49, 60-69 und 80-89 kleiner als 0,0001%. Für die Altersgruppen 10-19, 30-39, 50-59, 70-79 und 90+ liegt er bei 33%, 19%, 5%, 10% bzw. 11%.
Die altersabhängige Corona-Sterblichkeit (Mortalität)
Eine exponentiell-lineare Näherungsformel für die Mortalität pro 100.000 Einwohnern ist durch die folgende Beziehung gegeben:
(11)
Ausgedrückt in Prozentwerten lautet die Formel für die Mortalität p.a.:
(12)
Für den Altersbereich 5-80 bleibt der absolute Fehler unter 0,005%, für 80-89 und 90+ liegt er bei 0,012% bzw. 0,1%. Der relative Fehler liegt für die Altersgruppe 30-90+ unter 8%. Für die Altersgruppe 20-29 wird das Risiko um 23% überschätzt, für die Altersgruppen 10-19 und 0-9 um 17% bzw. 65% unterschätzt. Das allerdings auf einem sehr niedrigen absoluten Risikoniveau unter 0,0005%.
Nach vorstehender Approximationsformel verzehnfacht sich der Mortalitätswert p.a. pro 22 Lebensjahren. Verglichen mit einem 18-Jährigen hat demzufolge ein 40-Jähriger ein 10-fach, ein 62-Jähriger ein 100-fach und ein 84-Jähriger ein 1000-fach höheres Corona-Sterberisiko p.a.. Um das richtig einzuordnen, muss man erwähnen, dass das absolute Risiko von 18-Jährigen bei etwa 0,0005% liegt, das von 84%-Jährigen bei 0,5%.
Wegen kann man ebenfalls konstatieren, dass sich das Corona-Sterberisiko p.a. pro etwa 6,5 Lebensjahren verdoppelt.
Das altersabhängige Corona-Infektionsrisiko
Eine passable exponentiell-lineare Näherungsformel für das Infektionsrisiko in Prozent kann folgendermaßen formuliert werden:
(13)
Für die Altersgruppen 30-39, 60-69 und 70-79 bleibt der absolute Fehler unter 0,25%, für 50-59 liegt er bei 0,7%, für 10-29 und 80-89 bei max. 2,2%. Etwas größer ist die Abweichung für die Altersgruppen 0-9 (8,5%) und 90+ (4,3%). Der relative Fehler bleibt für die Altersgruppe 10-90 unter 30%.
Die etwas größeren Abweichungen der linearen Näherungsformel bei den Älteren werden auf Basis der untenstehenden exponentiell-kubischen Approximation vermieden:
(14)
Für den Altersbereich 40-90+ bleibt der absolute Fehler der kubischen Näherung unter 0,6%. Die Approximation liegt für die Altersgruppen 0-39 um max. 3,3% daneben. Dabei bleibt der relative Fehler zwischen 20% (10-19) und 45% (0-9). Deutlich kleiner ist der relative Fehler für die Altersgruppen 40-59 (max. 2,4%) sowie 60-69 und 80-89 (<1%). Für die Altersgruppen 70-79 und 90+ liegt er bei max. 12,5%.
Im Unterschied sowohl zur Letalität wie auch zur Mortalität, die beide mit zunehmendem Alter exponentiell wachsen, sehen wir bezüglich des Infektionsrisikos ein gegenteiliges Verhalten: Je höher das Alter, desto geringer die Infektionswahrscheinlichkeit. Diese Abhängigkeit ist zwar nicht so stark und eindeutig ausgeprägt, sie führt aber dennoch dazu, dass das Infektionsrisiko mit dem Alter signifikant zurückgeht. Vermutlich deswegen, weil Ältere im Allgemeinen weniger Kontakte haben oder sich bei ihren Kontakten besser schützten.
Ganz grob kann man sagen, dass sich die Infektionswahrscheinlichkeit p.a. pro 30 Lebensjahren in etwa halbiert. Ein Blick auf die Zweierpotenz-Näherungsformel macht das unmittelbar klar.
(15)
Für die Lebensalter 20 – 80 ist die Approximation nahe an der Realität.
Bestimmung der Letalitäten für Geimpfte und Ungeimpfte bei unzureichender Erfassung des Impfstatus
Die Letalität für alle Infizierten sowie die Letalitäten für die infizierten Geimpften
und Ungeimpften
sind folgendermaßen definiert:
(16)
Der Wert für ergibt sich direkt aus den Statistiken des RKI. Da indessen die Impfstatus der Infizierten und der Verstorbenen in 2021 nicht konsequent erfasst wurden (jedenfalls wurden diese Zahlen vom RKI nicht veröffentlicht), können die Letalitätswerte der Geimpften und der Ungeimpften nicht unmittelbar aus dem Datenmaterial des RKI bestimmt werden. Über einen kleinen Umweg ist es indes möglich, die Zahl der infizierten und verstorbenen Geimpften,
und
, zu berechnen. Gleiches geht auch für die Ungeimpften (
und
).
Bei bekannter Impfquote und Wirksamkeit des Impfstoffs greifen wir dazu auf Formel (5) in [11] (Der Effekt der Corona-Impfung auf die Fallzahlen – sumymus blog) zurück und erhalten
(17)
Dabei sind und
die entsprechenden Impfstoff-Wirksamkeiten für den Schutz vor Infektion und den Schutz vor Tod.
Für die Anzahl der Ungeimpften ergibt sich analog
(18)
(19)
Die unbekannten Letalitäten der Geimpften und der Ungeimpften können nun leicht aus den vorstehenden Formeln bestimmt werden:
(20)
Und somit
(21)
sowie
(22)
(23)
Das Verhältnis der beiden Letalitäten ergibt sich zu
(24)
Datengrundlage für die Berechnung der Letalitäten
Die altersgruppenspezifischen Impfquoten und Wirksamkeiten sind grundsätzlich bekannt. Die Impfkampagne begann Anfang 2021, so dass im Hinblick auf die Anwendung der obigen Formel zur Bestimmung der Letalitätswerte für das Gesamtjahr mittlere Impfquoten abgeschätzt werden müssen. Dasselbe gilt für die Wirksamkeiten bezüglich es Infektionsschutzes und des Schutzes vor Tod. Die betreffenden Annahmen sind in Tab. 1 (s.o.) aufgelistet.
Bestimmung der Todesfallzahlen für Geimpfte und Ungeimpfte
Nach obigen Formeln erhalten wir für die Anzahl der verstorbenen Geimpften und Ungeimpften zusammenfassend die folgenden Beziehungen:
(25)
Die simple Mathematik zum Effekt von Massenimpfungen
Der Quotient bringt die Wirkung der Massenimpfung in kompakter Form zum Ausdruck:
(26)
Für und für
gibt es keine verstorbenen Geimpften, für
gibt es keine Ungeimpften.
Das relative Sterberisiko von Geimpften im Vergleich zu Ungeimpften ist . Daher sind die Todesfallzahlen bei Geimpften und Ungeimpften gleich hoch, wenn das Zahlenverhältnis zwischen Geimpften und Ungeimpften reziprok proportional zum Verhältnis der Todesfallrisiken ist, wenn also
(27)
Die Anzahl der Todesfälle von Ungeimpften überwiegt, sofern die linke Seite kleiner ist. Das ist sicher dann der Fall, wenn die Impfquote die Wirksamkeit nicht übersteigt. Umgekehrt gibt es mehr Todesfälle bei Geimpften, wenn das Zahlenverhältnis zwischen Impfquote und „Nicht-Impfquote“ über den Wert für das Risikoverhältnis auf der rechten Seite hinauswächst.
Der Zusammenhang gilt auch ganz allgemein für Infizierte oder Hospitalisierte.
(28)
Herleitung der zu erwartenden Infektions- und Todesfallzahlen bei einer geänderten Impfquote und Wirksamkeit des Impfstoffs
Es stellt sich die Frage, wie sich denn die Todesfallzahlen in 2021 entwickelt haben würden, wenn die Imfpquote höher oder niedriger gewesen oder die Wirksamkeit des Impfstoffs eine andere gewesen wäre. Natürlich ist diese Frage spekulativ. Dennoch kann man sich der Antwort nähern und begründete Aussagen zum Effekt solcher Änderungen auf die Todesfallzahlen ableiten. Ausgangspunkt ist das oben formulierte Invarianz-Postulat.
Im Folgenden bestimmen wir die zu erwartenden Infektions- und Todesfallzahlen bei modifizierter Impfquote und Impfstoffwirksamkeit. Das versetzt uns in die Lage, Was-Wäre-Wenn-Analysen durchzuführen.
Grundformeln für Ableitung der hypothetischen Infektions- und Todesfallzahlen
Die modifizierte Impfquote bezeichnen wir mit , die geänderte Wirksamkeit für den Schutz vor Infektion nennen wir
. Der Einfachheit halber verzichten wir dabei auf das Subskript, wenn es aus dem Zusammenhang heraus keine Verwechslungen geben kann;
meint also
.
Wir fragen nach dem formelmäßigen Zusammenhang zwischen den neuen Infektions- und Todesfallzahlen bei der Impfquote und der Infektionsschutz-Wirksamkeit
und den Bezugswerten bei der Impfquote
und der Wirksamkeit
. Dabei setzen wir eine unveränderte Wirksamkeit
bezüglich des Schutzes vor Tod voraus. Die neuen Infektions- und Todesfallzahlen bezeichnen wir mit
,
,
, die Bezugswerte mit
,
,
.
Wir erhalten die folgenden Beziehungen:
(29)
Erläuterung und Plausibilisierung der Beziehungen
Zur Motivation der Formeln betrachten wir eine Kohorte von 1000 Personen, 400 Geimpften und 600 Ungeimpften. Die Impfquote ist daher 40%. Der Infektionsschutz möge bei 60% liegen. Nehmen wir an, 30 Ungeimpfte seien infiziert. Demnach gibt es nun also infizierte Geimpfte. Wenn wir nun die Impfquote auf 70% erhöhen, dann haben wir 700 Geimpfte und nur noch 300 Ungeimpfte. Entsprechend geht die Zahl der infizierten Ungeimpften auf
zurück. Zugleich steigt die Anzahl der infizierten Geimpften auf
.
Die Anzahl der infizierten Ungeimpften verändert sich demnach proportional zur Quote der Nicht-Geimpften, wie man das intuitiv erwartet. Im Beispiel ist das der Faktor . Auf der anderen Seite wird die Anzahl der infizierten Geimpften entsprechend im Verhältnis der Impfquoten
erhöht.
Wenn sich die Wirksamkeit verändert, hat das offensichtlich keinen Einfluss auf die Anzahl der infizierten Ungeimpften. Doch wie verhält es sich bei den Geimpften? Gehen wir noch einmal zum obigen Beispiel und lassen nun die Impfquote konstant bei 40%, verändern aber die hypothetische Wirksamkeit von 60% auf 80%. Im Ergebnis sinkt die Anzahl der infizierten Geimpften auf . Ihre Anzahl verändert sich daher proportional zum Verhältnis der Restrisiken. Im Beispiel
. Zugleich sinkt die Gesamtzahl der Infizierten von
auf
.
Wenn sowohl die Impfquote als auch die Wirksamkeit modifiziert werden, so ändert sich gegenüber den beiden Beispielen nichts bei den Ungeimpften, ihre Zahl geht auf zurück. Die Zahl der infizierten Geimpften verändert sich dagegen proportional zum Verhältnis
auf
.
Werfen wir noch einen kurzen Blick auf die Gesamtzahl der Infizierten. Im ersten Beispiel sinkt sie von auf
. Das ist das Verhältnis
. Analog im zweiten Beispiel: Die Gesamtzahl der Infizierten verringert sich von
auf
und geht damit proportional zum Verhältnis
zurück. Schließlich stellt sich im dritten Fall bei der gleichzeitigen Veränderung von Impfquote und Wirksamkeit die neue Anzahl der Infizierten, also
, entsprechend dem Verhältnis
ein.
Formeln für die Bestimmung der Infektionszahlen Geimpfter und Ungeimpfter
Kommen wir zurück zur Berechnung der Anzahl der infizierten Geimpften und Ungeimpften. Für die Fallzahlen bei Änderung der Impfquote und der Wirksamkeit erhalten wir
(30)
Formeln für die Bestimmung der Todesfallzahlen Geimpfter und Ungeimpfter
Im Weiteren können wir auf Basis obiger Formeln auch die Höhe der zu erwartenden Todesfallzahlen der infizierten Geimpften und Ungeimpften nach einer Modifikation von Impfquote und Wirksamkeit direkt aus den Werten für die Gesamtzahl der Infizierten vor der Veränderung errechnen. Wie oben bezeichnen wir die neuen Todesfallzahlen mit ,
,
und die Bezugswerte mit
,
,
.
(31)
(32)
Diese Beziehungen können wir nur deswegen so formulieren, weil sich die Letalitäten für die Geimpften und Ungeimpften im betrachteten Szenario nicht verändern, weil also und
. Das Invarianz-Postulat wurde oben erläutert. Für die Gesamtletalität gilt dagegen
.
Die Bestimmung der Gesamtletalität bei geänderter Impfquote und Wirksamkeit
Zur Bestimmung von gehen wir aus von
(33)
Wegen
(34)
bekommen wir für den Ausdruck
(35)
Die Gesamtletalität bei geänderter Impfquote und gleicher Wirksamkeit
Für vereinfacht sich die
-Formel auf
(36)
womit sich der Zusammenhang zwischen den nach der Modifikation zu erwartenden Todesfallzahlen und den ursprünglichen Infektionszahlen
für diesen Spezialfall deutlich kürzer fassen lässt:
(37)
Quellen
[1] Robert Koch-Institut, COVID-19_Todesfälle nach Sterbedatum https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Projekte_RKI/COVID-19_Todesfaelle.html
[2] Robert Koch-Institut, COVID-19_Fälle nach Altersgruppe und Meldedatum
RKI – Coronavirus SARS-CoV-2 – COVID-19-Fälle nach Altersgruppe und Meldewoche (Tabelle wird jeden Donnerstag aktualisiert)
[3] Robert Koch-Institut, Coronavirus Situationsberichte, Wochenbericht https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Situationsberichte/Wochenbericht/Wochenberichte_Tab.html
[4] Robert Koch-Institut, Coronavirus Inzidenzen und Impfstatus https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Daten/Inzidenz_Impfstatus.html
[5] Robert Koch-Institut, Coronavirus Fallzahlen https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Daten/Fallzahlen_Kum_Tab.html
[6] Robert Koch-Institut, Coronavirus Impfquotenmonitoring https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Daten/Impfquotenmonitoring.html
[7] Robert Koch-Institut, Inzidenzen der symptomatischen und hospitalisierten COVID-19-Fälle nach Impfstatus https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Daten/Inzidenz_Impfstatus.html
[8] Wie lange schützt der Impfstoff von Biontech, Moderna und Astrazeneca | Spektrum
[9] Das Coronavirus: Harmlos? Bedrohlich? Tödlich? – sumymus blog
[10] Gibt es eine Korrelation zwischen Impfquote und Inzidenz?
[11] Der Effekt der Corona-Impfung auf die Fallzahlen – sumymus blog
[12] Wer treibt die Infektionen? Ungeimpfte oder Geimpfte? – sumymus blog